Динамическое программирование

Пример. Задача определения авиамаршрута из Москвы в Токио минимальной стоимости. Пусть даны цены на имеющиеся авиарейсы.

№	Рейс	цена	№	Рейс	цена
1	Москва - Новосибирск	55	8	Иркутск - Якутск	30
2	Москва - Якутск	155	9	Иркутск - Владивосток	90
3	Москва - Иркутск	130	10	Якутск - Хабаровск	30
4	Новосибирск - Иркутск	75	11	Якутск - Владивосток	70
5	Новосибирск - Владивосток	170	12	Хабаровск - Владивосток	35
6	Новосибирск - Якутск	90	13	Хабаровск - Токио	80
7	Иркутск - Хабаровск	50	14	Владивосток - Токио	40

Представим таблицу в виде ориентированного нагруженного графа (рис.1), вершины которого соответствуют городам, дуги – авиарейсам между ними, указанным в таблице, а их длины равны соответствующим ценам на авиарейсы.

Рис. 1.

Отметим, что полученный связный ориентированный граф не имеет петель и циклов, то есть является сетью. Вершина М (Москва) – вход, а вершина Т(Токио) – выход. Таким образом, задача состоит в определении пути минимальной длины от входа до выхода данной сети.

Определим ранги вершин рассматриваемой сети. В соответствии с ростом ранга занумеруем вершины: - Москва, - Новосибирск , - Иркутск, - Якутск, - Хабаровск, - Владивосток, - Токио.

Найдем минимальный путь от данной вершины до выхода.

Определим последовательно длину минимального маршрута от вершины до выхода , начиная с вершины максимального ранга 6.

Шаг 1. Очевидно, что .

Шаг 2. Из вершины ( В) ранга 5 выходит только одна дуга – рейс Владивосток – Токио длины . Следовательно, длина оптимального маршрута из Владивостока в Токио . Причем оптимальный маршрут проходит по дуге ( более того, он совпадает с этой дугой). Выделим эту дугу на рисунке жирной линией.

Рис. 5.

Шаг 3. Из вершины ( Хабаровск) ранга выходят две дуги: (Хабаровск –> Токио) длины и (Хабаровск –> Владивосток) длины . Оптимальный маршрут из Хабаровска в Токио либо проходит через Владивосток, либо непосредственно ведет в Токио и его длина равна минимальной длине этих двух маршрутов: .

Как видим, оптимальным является маршрут ( Х –> В –> Т ) длины ), проходящий по дуге (Х –> В), которую мы также выделяем жирной линией на следующем рисунке.

Рис. 6.

Шаг 4. Находим оптимальный маршрут из вершины (Якутск) ранга 3 (до Токио). Из дуга – (Я – Х) длины ведет в Хабаровск, оптимальный маршрут из которого и его длина найдены выше. Если проходит по этой дуге, то его длина равна сумме . Если же оптимальный маршрут из проходит по дуге – (Я – В) длины через Владивосток (оптимальный маршрут из которого и его длина уже найдены), то он имеет длину . Следовательно, имеет длину , и пролегает по дуге (Я –> Х):

Рис. 7.

Шаг 5. Из вершины ( Иркутск) ранга 2 выходят три дуги: - (И –> Я) длины , - (И –> Х) длины и – (И –> В) длины . Следовательно, оптимальный маршрут из Иркутска в Токио имеет длину и содержит дугу , которую мы снова выделяем жирной линией.

Рис. 8.

Шаг 6. Из вершины (Новосибирск) ранга 2 выходят три дуги: (Н –> Я) длины , (Н –> И) длины и (Н –> В) длины . Следовательно, оптимальный маршрут из Иркутска в Токио имеет длину

и проходит по дуге , которую выделяем жирной линией на следующем рисунке.

Рис. 9.

Шаг 7. Итак, мы добрались до Москвы (вершины ранга 0). Имеется всего три дуги: (М –> Я) длины , (М –> И) длины и (М –> Н) длины , исходящие из . Следовательно, оптимальный маршрут имеет длину

и проходит по дуге , выделенную жирной линией на следующем рисунке.

Рис. 10.

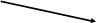
Двигаясь из вершины М по жирным дугам, получаем оптимальный маршрут (М осква – Новосибирск – Якутск – Хабаровск – Владивосток – Токио) из Москвы в Токио, длина (стоимость) которого равна .

Игровые методы и модели.