Биматричные игры

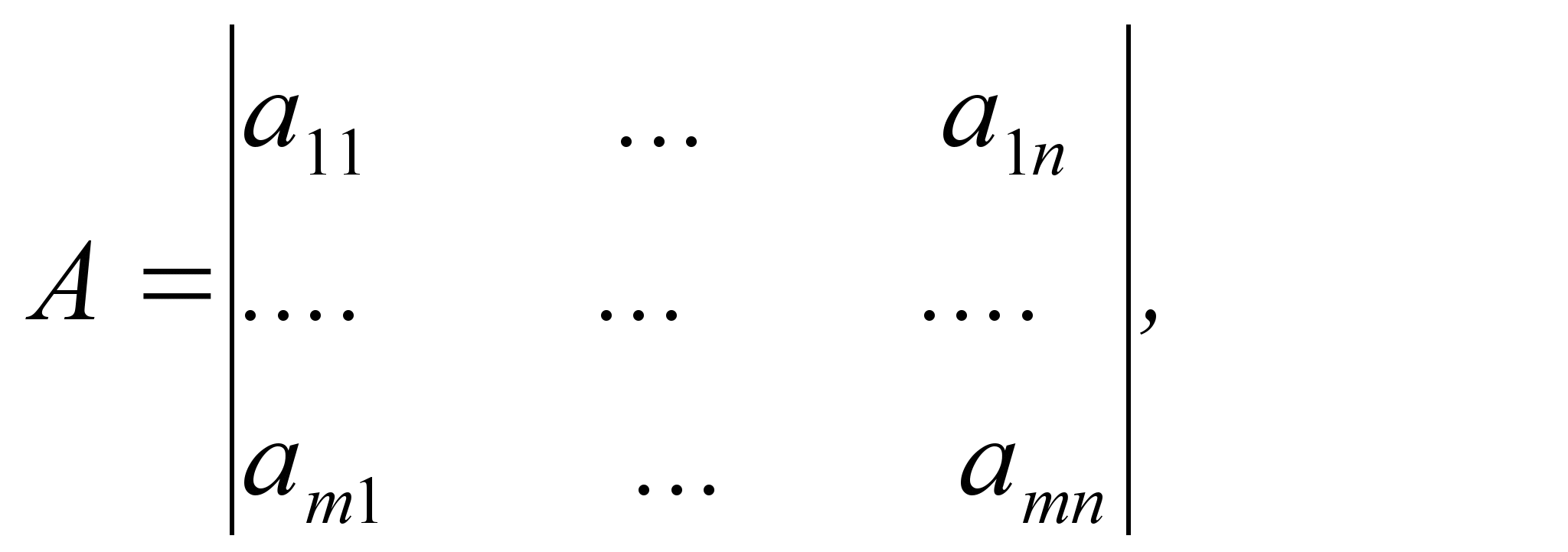
В биматричной игре игрок 1 имеет m чистых стратегий А_і,  а игрок 2 имеет n чистых стратегий В_j,  и в каждой ситуации (A_i, B_j) игрок 1 получает выигрыш a_ij, а игрок 2 – выигрыш b_ij. Теперь b_ij не обязано равняться (- a_ij ). Значение обеих функций выигрыша игроков естественно представить в виде пары матриц  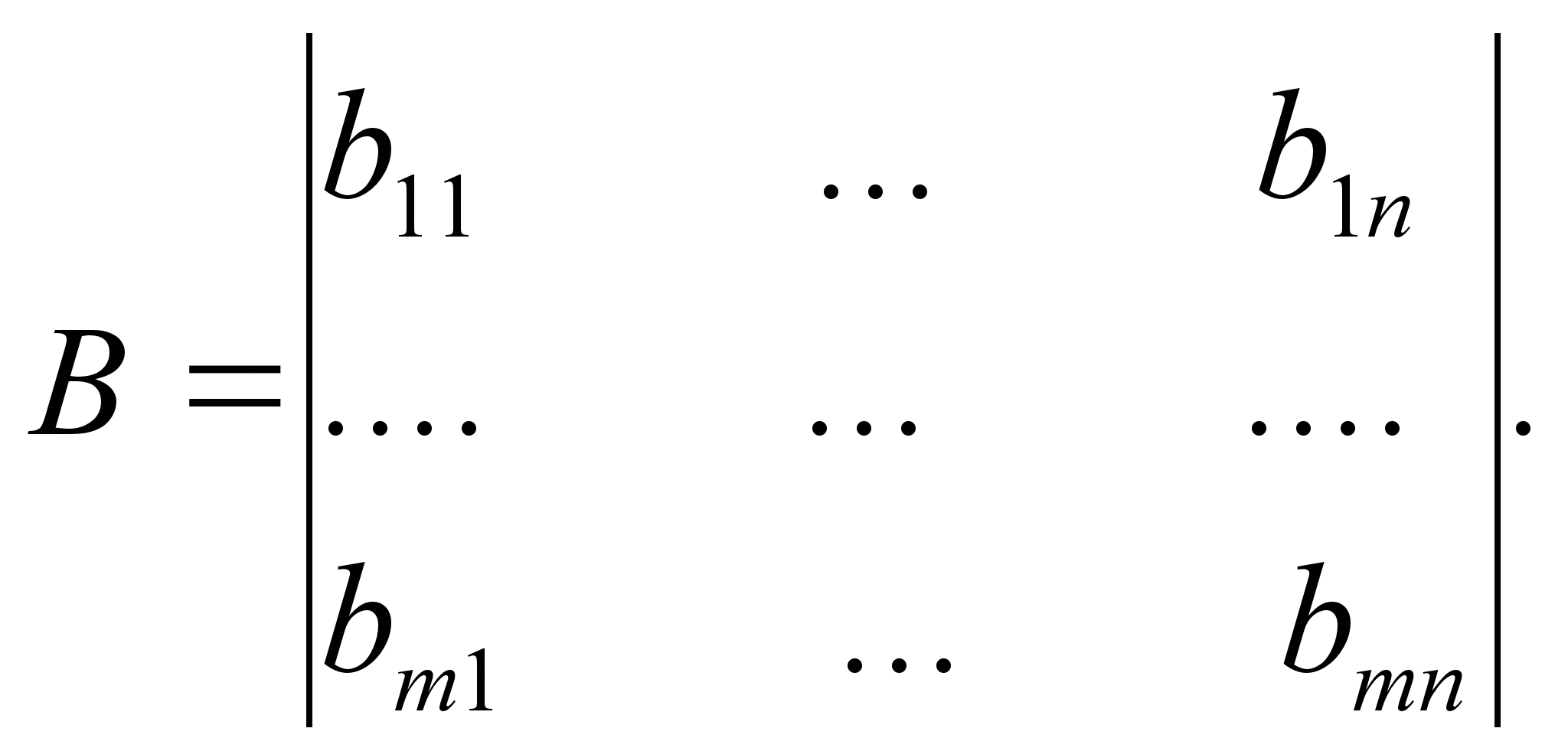 Поэтому такие игры и называются биматричными. Используют также запись платежных матриц А и В в следующем виде:

а11 b11	.........	a1n b1n
, ........	.........	........
am1 bm1	.........	amn bmn

где верхнее число в каждой клетке обозначает выигрыш первого игрока, а нижнее – выигрыш второго игрока.

Равновесие по Нэшу Ситуация в биматричной игре (A_i, B_j) называется равновесной по Нэшу, если стратегия A_i 1-го игрока является наилучшим ответом на стратегию B_j 2-го игрока, и, одновременно, стратегия B_j 2-го игрока является наилучшим ответом на стратегию A_i 1-го игрока.

Пример. Определим ситуации равновесные по Нэшу в игре, заданной матрицами А и В.

Для этого в каждом столбце матрицы A найдем максимальный элемент. Эти элементы выделены в матрице A. Их положение соответствует наилучшим ситуациям для 1-го игрока, когда второй игрок выбрал стратегию j соответственно. Затем в каждой строке матрицы B выберем наибольший элемент. Эти элементы выделены в матрице B. Их положение будет определять наилучшие ситуации 2-го игрока, когда первый игрок выбрал стратегию i, соответственно. Платежная матрица игрока А:

3	6	0
0	0	-2
4	7	1

Платежная матрица игрока B:

5	-4	0
0	8	2
0	-1	3

Таким образом, найдена равновесная ситуация (3;3). В равновесной ситуации (3,3) игрок 1 выигрывает 1 единицу, а игрок 2 выигрывает 3 единицы.

Эффективность по Парето

Ситуация в биматричной игре (A_i, B_j) называется эффективной по Парето, если не существует другой ситуации в этой игре, в которой оба игрока выигрывают не меньше, и хотя бы один из них выигрывает больше. В рассмотренном выше примере эффективными по Парето являются ситуации (1,1), (2,2) , (3,1) , (3,2).