- •Фильтры нижних частот
- •Коэффициенты полинома передаточной функции для фильтров 2, 4 и 6 порядка
- •Преобразование нижних частот в полосу частот
- •Полосно-подавляющие фильтры
- •Реализация фильтров на операционных усилителях.
- •Активный фнч второго порядка Саллена-Ки
- •Активный полосовой фильтр с многопетлевой обратной связью
- •Активный полосно-подавляющий фильтр с многопетлевой отрицательной обратной связью
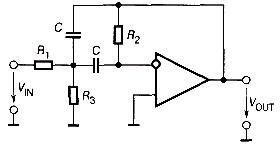
- •Активный заграждающий фильтр с двойным т-образным мостом
- •Фазовые фильтры
Реализация фильтров на операционных усилителях.
С ростом порядка фильтра его фильтрующие свойства улучшаются. На одном ОУ достаточно просто реализуется фильтр второго порядка. Для реализации фильтров нижних частот, верхних частот и полосовых широкое применение нашла схема фильтра второго порядка Саллена-Ки. На рисунке приведен ее вариант для ФНЧ.
Отрицательная
обратная связь, сформированная с помощью
делителя напряжения
![]() обеспечивает коэффициент усиления,
равный .
обеспечивает коэффициент усиления,
равный .
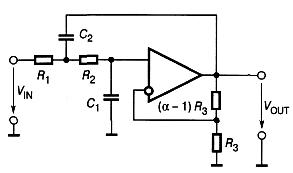
Активный фнч второго порядка Саллена-Ки
Положительная обратная связь обусловлена наличием конденсатора С2. Передаточная функция фильтра имеет вид:
![]()
Расчет
схемы существенно упрощается, если с
самого начала задать некоторые
дополнительные условия. Можно выбрать
коэффициент усиления![]() Тогда
Тогда
![]() и резистивный делитель напряжения в
цепи отрицательной обратной связи можно
исключить. ОУ оказывается включенным
по схеме неинвертирующего повторителя.
В простейшем случае он может быть даже
заменен эмиттерным повторителем на
составном транзисторе. При
и резистивный делитель напряжения в
цепи отрицательной обратной связи можно
исключить. ОУ оказывается включенным
по схеме неинвертирующего повторителя.
В простейшем случае он может быть даже
заменен эмиттерным повторителем на
составном транзисторе. При
![]() передаточная
функция фильтра принимает вид:
передаточная
функция фильтра принимает вид:
![]()
Для
расчета фильтра можно задать значения
резисторов
![]() и
по приведенным формулам вычислить
значения
и
по приведенным формулам вычислить
значения
![]() Однако,
в связи с тем, что конденсаторы, как
правило, приходится выбирать из ряда
Е12, где отношение соседних емкостей
составляет 1.21, или даже из ряда Е6, где
отношение соседних емкостей составляет
1.47, удобнее задаваться значениями
емкостей конденсаторов и вычислять
необходимые значения сопротивлений
резисторов. Расчет следует начинать с
выбора емкостей
Однако,
в связи с тем, что конденсаторы, как
правило, приходится выбирать из ряда
Е12, где отношение соседних емкостей
составляет 1.21, или даже из ряда Е6, где
отношение соседних емкостей составляет
1.47, удобнее задаваться значениями
емкостей конденсаторов и вычислять
необходимые значения сопротивлений
резисторов. Расчет следует начинать с
выбора емкостей
![]() Для
того чтобы получить приемлемые
сопротивления резисторов, рекомендуется
взять
Для
того чтобы получить приемлемые
сопротивления резисторов, рекомендуется
взять
![]() Считая,
что емкости конденсаторов
Считая,
что емкости конденсаторов
![]() выбраны,
получим для заданных значений
выбраны,
получим для заданных значений
![]() и
и
![]()
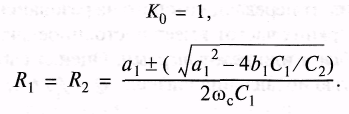
Чтобы значения R1 и R2 были действительными, должно выполняться условие
![]()
Расчеты
можно упростить, положив
![]() В
этом случае для реализации фильтров
различного типа необходимо изменять
значение коэффициента
В
этом случае для реализации фильтров
различного типа необходимо изменять
значение коэффициента
![]() Передаточная
функция фильтра будет иметь вид
Передаточная
функция фильтра будет иметь вид
![]()
Отсюда получим
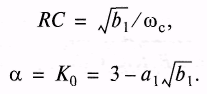
Из последнего соотношения видно, что коэффициент определяет добротность полюсов и не влияет на частоту среза. Величина в этом случае определяет тип фильтра.
На рисунке приведена схема ФНЧ второго порядка с многопетлевой отрицательной обратной связью (фильтр Рауха).

Схема ФНЧ второго порядка с многопетлевой отрицательной обратной связью (фильтр Рауха)
Здесь ОУ используется в инвертирующем включении. Передаточная функция этого фильтра
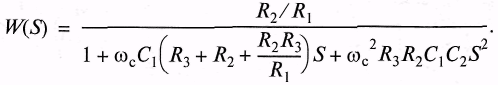
Приравняв коэффициенты этой передаточной функции к коэффициентам ФНЧ получим
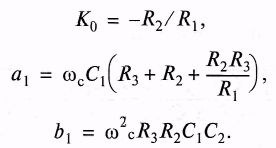
Для определения сопротивлений резисторов при выбранных емкостях конденсаторов решим уравнения относительно сопротивлений
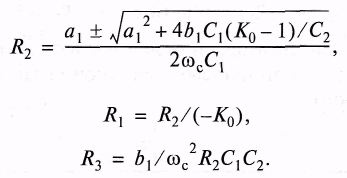 ■
■
Для
того чтобы значение сопротивления
![]() было
вещественным, должно выполняться
условие
было
вещественным, должно выполняться
условие![]()
При
его выполнении в процессе расчета
фильтра не следует выбирать отношение
![]() много
большим величины, стоящей справа.
Характеристики фильтра мало зависят
от точности подбора номиналов его
элементов, поэтому рассмотренная схема
может быть рекомендована для реализации
фильтров с высокой добротностью.
много
большим величины, стоящей справа.
Характеристики фильтра мало зависят
от точности подбора номиналов его
элементов, поэтому рассмотренная схема
может быть рекомендована для реализации
фильтров с высокой добротностью.
При приеме слабых сигналов смещение нуля операционных усилителей, входящих в состав фильтров на вышеприведенных схемах накладываясь на входной сигнал, порождает ошибку, поэтому очень интересна схема ФНЧ, нечувствительная к смещению нуля ОУ. Эта схема приведена на рисунке.
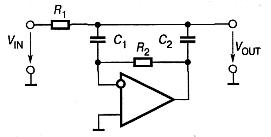
Схема активного ФНЧ второго порядка, нечувствительная к смещению нуля ОУ
Передаточная функция фильтра при условии, что он работает на холостом ходу, имеет вид:
![]()
Выбрав
емкости конденсаторов
![]() найдем
сопротивления резисторов.
найдем
сопротивления резисторов.

Поменяв местами сопротивления и конденсаторы в схеме ФНЧ второго порядка Саллена-Ки получим фильтр верхних частот.

Активный ФВЧ второго порядка
Его передаточная функция имеет вид:
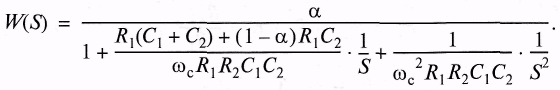
Для
упрощения расчетов положим
![]() При
этом получим следующие формулы:
При
этом получим следующие формулы:
![]()
Поменяв местами конденсаторы и резисторы в схеме фильтра Рауха получим фильтр верхних частот с многопетлевой обратной связью передаточная функция которого
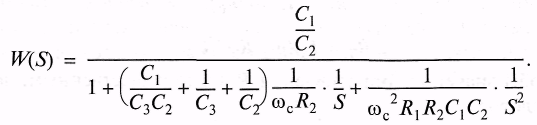
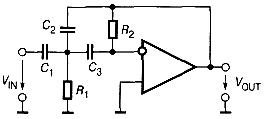
Фильтр верхних частот второго порядка с многопетлевой обратной связью
Из-за необходимости большого количества конденсаторов эта схема применяется сравнительно редко.
Если спад АЧХ фильтра второго порядка оказывается недостаточно крутым, следует применять фильтр более высокого порядка. Для этого последовательно соединяют звенья, представляющие собой фильтры первого и второго порядка. В этом случае АЧХ звеньев фильтра перемножаются (в логарифмическом масштабе — складываются).
Следует иметь в виду, что последовательное соединение, например, двух одинаковых фильтров Баттерворта второго порядка (как и фильтров любого другого типа) не приведет к получению фильтра Баттерворта четвертого порядка. Результирующий фильтр будет иметь другую частоту среза и другую частотную характеристику.
Поэтому необходимо задавать такие коэффициенты звеньев фильтра, чтобы результат перемножения их частотных характеристик соответствовал желаемому результату.
Полосовой фильтр второго порядка можно реализовать на основе схемы Саллена-Ки.
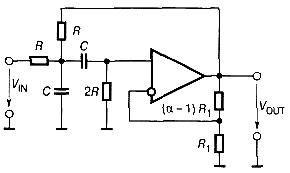
Схема активного полосового фильтра второго порядка
Передаточная функция фильтра имеет вид:
![]()
Приравнивая коэффициенты этого выражения к коэффициентам передаточной функции (см. полосовой фильтр) получим формулы для расчета параметров фильтра:
![]()
Недостаток
схемы состоит в том, что коэффициент
усиления на резонансной частоте
![]() и добротность
и добротность
![]() не
являются независимыми друг от друга.
Достоинство схемы — ее добротность
зависит от параметра ,
тогда как резонансная частота от этого
параметра не зависит.
не
являются независимыми друг от друга.
Достоинство схемы — ее добротность
зависит от параметра ,
тогда как резонансная частота от этого
параметра не зависит.
При
![]() коэффициент
усиления становится бесконечно большим
и возникает генерация. Чем ближе
коэффициент
усиления становится бесконечно большим
и возникает генерация. Чем ближе
![]() к
трем, тем критичнее точность его
установки.
к
трем, тем критичнее точность его
установки.
Многопетлевую отрицательную обратную связь можно использовать и для построения полосовых фильтров. Соответствующая схема приведена ниже. Ее передаточная функция имеет вид