Занятие 7

Активные электрические фильтры на ОУ

B электрических, радиотехнических, телекоммуникационных и телеметрических системах и устройствах, работающих на принципах частотного разделения сигналов, часто решается задача: из смеси сигналов, занимающих в совокупности широкую полосу частот, выделить те или иные составляющие или их определенные комбинации. Сигналы заданной частоты или заданной полосы частот выделяют при помощи частотных электрических фильтров.

K частотным электрическим фильтрам предъявляются два основных требования. B одной области частот, которая называется полосой пропускания (или полосой прозрачности), составляющие частотного спектра выделяемого сигнала не должны ослабляться, а в другой, называемой полосой задерживания (заграждения, подавления, режекции), их ослабление (затухание) должно быть не меньше определенного значения. Фильтр считают идеальным, если в полосе пропускания ослабление отсутствует и фазово-частотная характеристика линейно (при этом условии нет искажения формы сигналов), a вне полосы пропускания все частотные составляющие полностью подавляются, Т. e. идеальные фильтры должны иметь прямоугольные амплитyдно-частотные характеристики (АЧХ) как на рисунках. Однако идеальные фильтры физически нереализуемы.

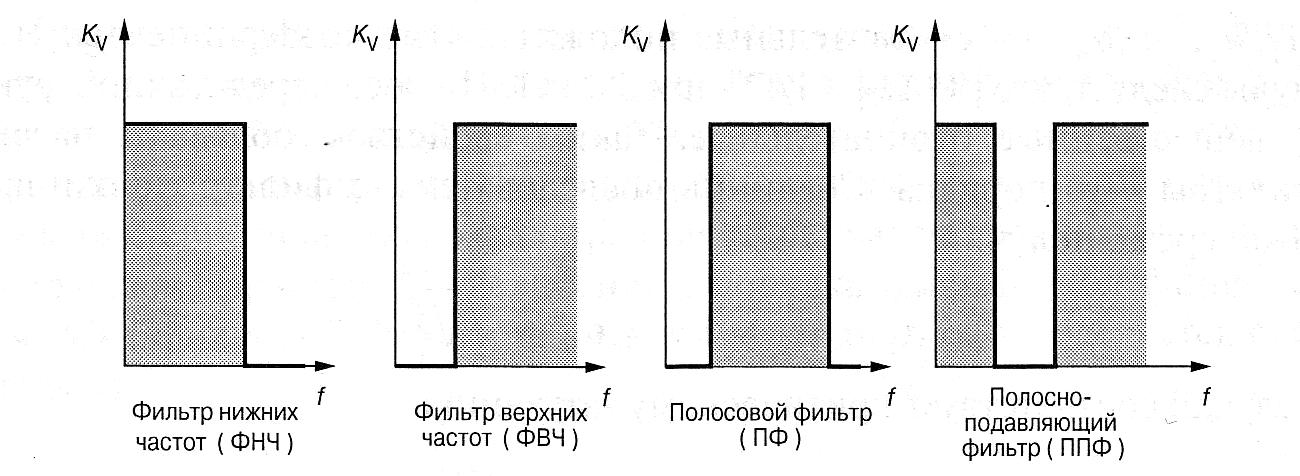
АЧХ идеaльных частoтны фильтpов

Фильтры можно классифицировать различным образом. Главный принцип классификации — диапазоны частот пропускания и подавления. B зависимости от пропускаемого спектра частот различают низкочастотные (фильтры нижних частот — ФНЧ), высокочастотные (фильтры верхних частот — ФВЧ), голосовые (ПФ), полосно-подавляющие (ППФ) избирательные (селективные — СФ) и заграждающие (режекторные — РФ) фильтры. Свойства линейных фильтров могут быть описаны передаточной функцией, которая равна отношению изображений по Лапласу выходного и входного сигналов фильтра.

Фильтры нижних частот

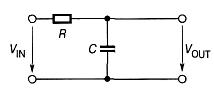
Простейший фильтр нижних частот первого порядка

Передаточная функция этого фильтра определяется выражением . Заменив s на j, получим частотную характеристику фильтра. Для реализации общего подхода целесообразно нормировать комплексную переменную s. Положим , где — круговая частота среза фильтра. В частотной области этому соответствует

Частота среза фильтра равна Отсюда получим и

Используя передаточную функцию для оценки зависимости амплитуды выходного сигнала от частоты, запишем

При т. е. для случая, когда частота входного сигнала

Это соответствует снижению коэффициента передачи фильтра с ростом частоты на 20 дБ/декада.

Если необходимо получить более быстрое уменьшение коэффициента передачи, можно включить n фильтров нижних частот последовательно. Передаточная функция такой системы имеет вид:

где — действительные положительные коэффициенты. Из этой формулы следует, что Полюса передаточной функции вещественные отрицательные. Таким свойством обладают пассивные -фильтры -го порядка. Соединив последовательно фильтры с одинаковой частотой среза, получим

Этот случай соответствует критическому затуханию.

Порядок фильтра определяет крутизну спада его АЧХ за полосой пропускания: чем выше порядок — тем круче спад.

Передаточная функция фильтра нижних частот (ФНЧ) в общем виде может быть записана как

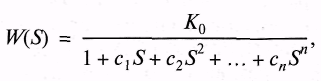
где — положительные действительные коэффициенты, — коэффициент усиления фильтра на нулевой частоте. Порядок фильтра определяется максимальной степенью переменной S. Для реализации фильтра необходимо разложить полином знаменателя на множители. Если среди нулей полинома есть комплексные, то рассмотренное ранее представление полинома не может быть использовано. В этом случае следует записать его в виде произведения квадратных трехчленов:

где — положительные действительные коэффициенты.

Отсюда вывод: любой полиномиальный фильтр (т. е. такой, что его передаточная функция представляет собой отношение полиномов) может быть образован соединением фильтров 2-го порядка.

Для полиномов нечетных порядков коэффициент равен нулю. Реализация комплексных нулей полинома в выражении на пассивных RС-цепях невозможна. Применение же катушек индуктивности в низкочастотной области нежелательно из-за больших габаритов и сложности их изготовления, а также из-за появления паразитных индуктивных связей. Схемы с операционными усилителями позволяют обеспечить комплексные нули в вышеприведенном полиноме без применения катушек индуктивности. Такие схемы называют активными фильтрами. Рассмотрим различные способы задания характеристик ФНЧ. Широкое применение нашли фильтры Бесселя, Баттерворта, Чебышева и эллиптические (Кауэра), названные так по виду полиномов передаточных функций, в разной степени аппроксимирующих АЧХ идеальных фильтров и отличающиеся друг от друга крутизной наклона амплитудно-частотной характеристики в начале полосы задерживания и степенью колебательности переходного процесса при ступенчатом входном воздействии. АЧХ фильтров четвертого порядка всех вышеперечисленных типов приведены на рисунке.

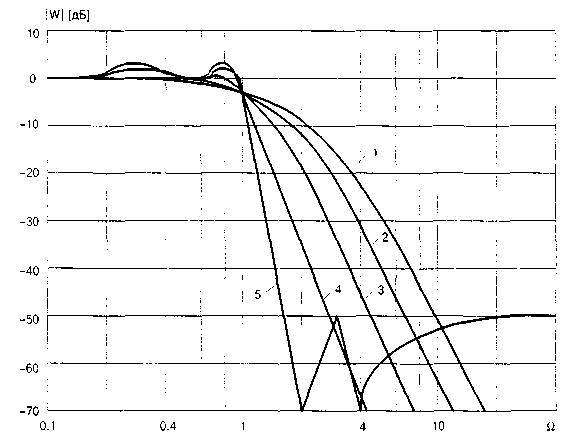
Амплитудно-частотные характеристики фильтров четвертого порядка: 1 — фильтр с критическим затуханием; 2 — фильтр Бесселя; 3 — фильтр Баттерворта;

4 — фильтр Чебышева с неравномерностью 3 дБ; 5 — эллиптический фильтр с неравномерностью в полосе пропускания 2 дБ и максимумами всплесков

в полосе заграждения —50 дБ

Амплитудно-частотная характеристика фильтра Баттерворта имеет наиболее длинный горизонтальный участок и резко спадает за частотой среза. Переходная характеристика такого фильтра при ступенчатом входном сигнале имеет колебательный характер. С увеличением порядка фильтра колебания усиливаются. АЧХ фильтра Баттерворта в случае n-го порядка определяется следующим образом

где п = 1,2, 3...

Фильтр с такой АЧХ физически нереализуем, поэтому приходится приближать ее полиномами.

Амплитудно-частотная характеристика фильтра Чебышева спадает более круто за частотой среза. В полосе пропускания она, однако, не монотонна, а имеет волнообразный характер с постоянной амплитудой, которая характеризуется неравномерностью q₁. При заданном порядке фильтра более резкому спаду амплитудно-частотной характеристики за частотой среза соответствует большая неравномерность в полосе пропускания. Колебания переходного процесса при ступенчатом входном воздействии сильнее, чем у фильтра Баттерворта. АЧХ фильтра Чебышева имеет вид

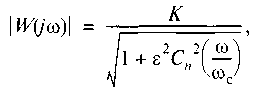
где п = 1, 2, 3...

Параметры  и К— постоянные числа, а С_п является полиномом Чебышева первого рода степени п и имеет вид

при

Эллиптический фильтр, называемый также фильтром Кауэра, характеризуется определенной неравномерностью АЧХ как в полосе пропускания, так и в полосе заграждения. Минимумы АЧХ в полосе пропускания обозначены — q₁ a максимумы в полосе заграждения — q₂. Спад АЧХ этого фильтра за полосой пропускания наиболее крутой по сравнению с фильтрами других типов. Передаточная функция эллиптического фильтра нижних частот имеет нули в числителе: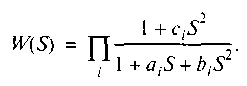

Фильтр Бесселя обладает оптимальной переходной характеристикой (минимальное время переходного процесса по сравнению с другими типами линейных фильтров). Причиной этого является пропорциональность фазового сдвига выходного сигнала фильтра частоте входного сигнала. Благодаря этому фильтр Бесселя воспроизводит сигналы, частотный спектр которых лежит в полосе пропускания фильтра, с наименьшими искажениями. Однако при равном порядке спад амплитудно-частотной характеристики фильтра Бесселя за полосой пропускания оказывается более пологим по сравнению с фильтрами Чебышева, Кауэра и Баттерворта. Передаточная функция фильтра Бесселя структурно имеет вид.

Тот или иной вид фильтра при заданном его порядке определяется коэффициентами полинома передаточной функции фильтра. В таблице даны эти коэффициенты для некоторых фильтров 2-го, 4-го и 6-го порядка.