Задание № 2

С помощью табличного процессора Microsoft Excel создать таблицу «Уравнивание теодолитного полигона» по варианту ______ и выполнить в ней вычисления. Создать по результатам вычислений диаграмму.

Для правильного вычисления дирекционных углов полигона необходимо построить схему полигона по исходным данным индивидуального задания на миллиметровой бумаге (правые углы откладываются от опорной линии по ходу часовой стрелки, левые – против хода часовой стрелки).

Алгоритм выполнения задания №2

• Запустить программу EXCEL.

• Создать по образцу ведомость уравнивания теодолитного полигона.

• Ввести в ведомость: номера точек, измеренные внутренние углы β, дирекционный угол твердой линии α, длины всех линий S_k и координаты твердых точек Хн, Ун, Хк, Ук. Использовать для ввода значений углов в градусах, минутах и секундах формат ячейки - Время и Тип – 37:30:55.

• Вычислить сумму измеренных углов в полигоне ∑βi и его периметр ∑S, используя функцию СУММ.

• Вычислить теоретическую сумму углов ∑βt в полигоне по формуле ∑βt=180(n-2), где n число точек полигона.

• Определить угловую невязку fβ=∑βi-∑βt , сравнить ее с допустимой, определяемой для углов измеренных тридцатисекундным теодолитом по формуле fβ_доп=±60n (сек), где fβ ≤ fβ_доп.

• Распределить угловую невязку поровну на все углы полигона (fβ/n).

• Вычислить дирекционные углы всех линий полигона по формулам:

• при измеренных правых углах - ,

• при измеренных левых углах -

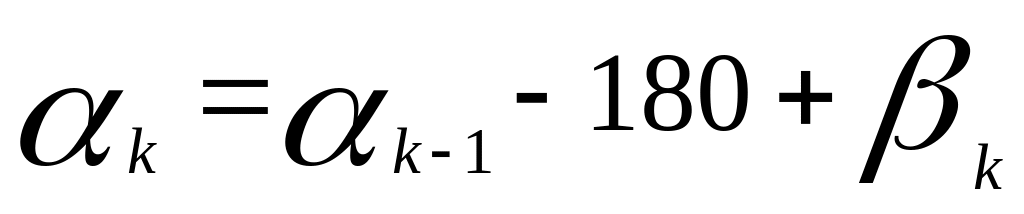
• Здесь k – номер линии, а β_k – внутренний угол в ее начале. Если при вычислении по первой формуле окажется α_k >360, то следует 180 не прибавлять, а вычитать.

• Выделить из дирекционных углов значения минут и секунд, используя функции EXCEL, соответственно, Минуты и Секунды.

• Вычислить по значениям минут и секунд десятичные доли градуса = (мин*60+сек)/3600.

• Определить дирекционные углы в градусах (прибавлением к целой части угла значения его доли).

• Перевести значения дирекционных углов в радианы, используя функцию EXCEL Радианы.

• Вычислить приращения координат по формулам: ∆Х_k = S_k*cos αk ∆У_k = S_k* sin αk, где αk – дирекционные углы в радианах.

• Вычислить сумму приращений координат ∑∆Х_k и ∑∆Y_k.

• Вычислить линейные невязки в приращениях координат по каждой оси по формулам: fx = Хн – Хк + ∑∆Х_k fy = Ун – Ук + ∑∆Y_k .

• Определить абсолютную и относительную невязку в периметре , сравнить ее с допустимой f ≥ f _доп, где f_доп=1500.

• Вычислить исправленные приращения координат по формулам: DХ_k = ∆Х_k - fx / ∑S * S_k DY_k = ∆У_k - fy / ∑S * S_k .

• Вычислить сумму исправленных приращений координат ∑DХ_k и ∑DY_k.

• Вычислить линейные невязки в исправленных приращениях координат по каждой оси по формулам: fx = Хн – Хк + ∑DХ_k fy = Ун – Ук + ∑DY_k , где fx =0, fy =0.

• Вычислить координаты всех точек полигона по формулам:

X_k+1 =X_k + DХ_k Y_k+1 = Y_k + DY_k .

• Выполнить контрольную проверку вычисления координат. Координаты конечной точки полигона должны получиться равными исходным ее значениям. Или иначе: fx =Хн – Хк + ∑DХ = 0 fy =Ун – Ук + ∑DY = 0.

• Сохранить изменения в файле.

• Завершить работу с MS Excel.

Типовой пример по уравниванию теодолитного полигона приведен в приложении № 2.