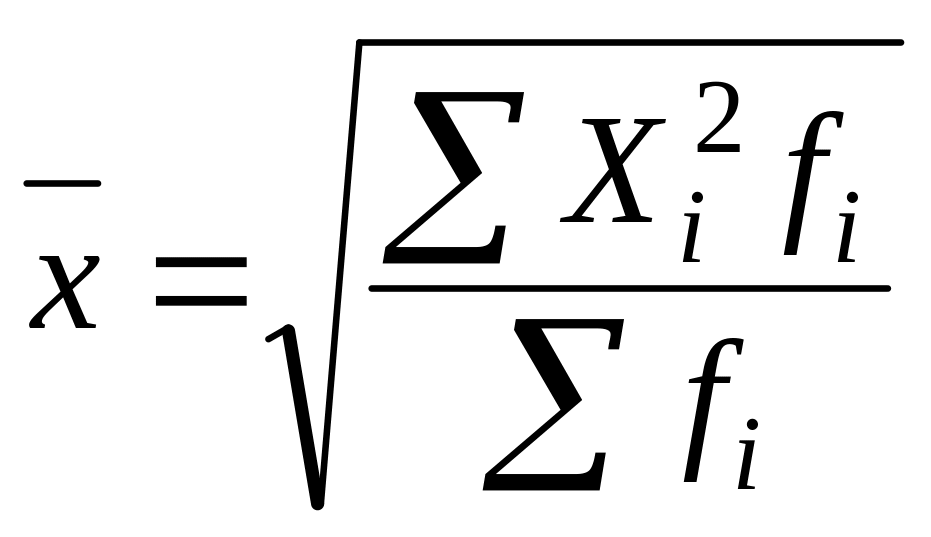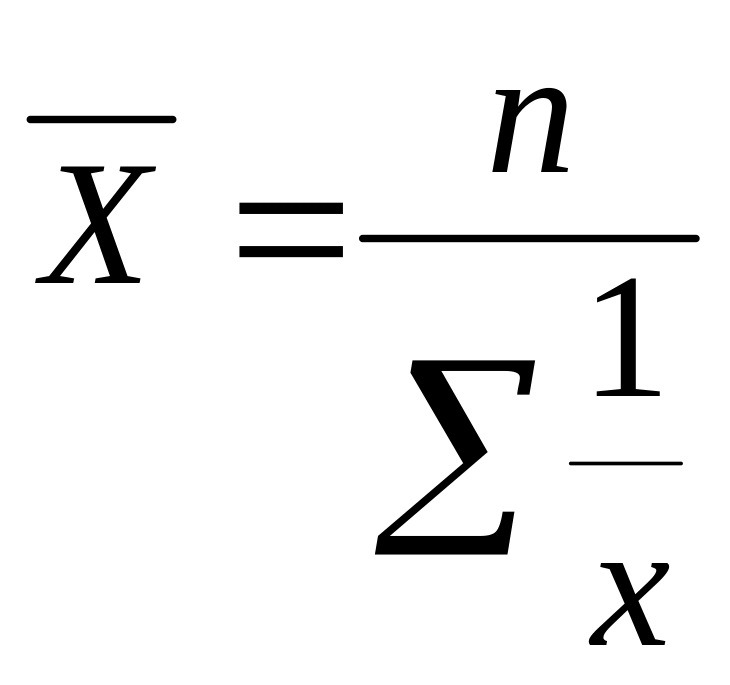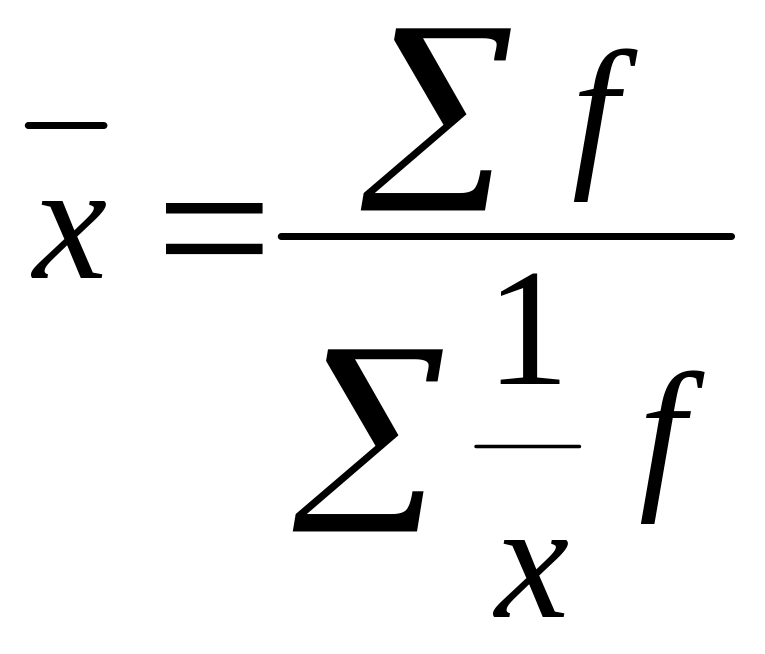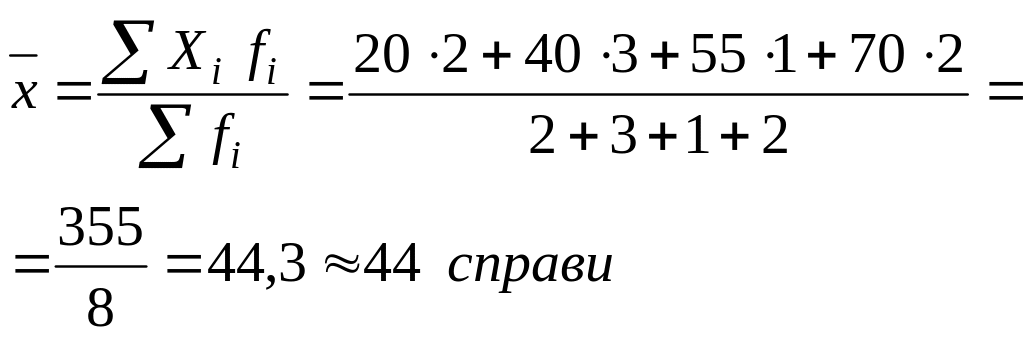2. Види середніх величин

Всі середні величини розподіляються на два класи:

			Середні
Ступеневі					Структурні
Арифметична
Геометрична								Мода
Квадратична
Гармонійна								Медіана
Кубічна
та ін.

Ступеневі середні залежно від наявної вихідної інформації можуть бути простими та зваженими.

Проста середня застосовується коли представлені незгруповані дані і має такий вигляд:

,

де – середня певного ступеня; m – показник ступеня середньої, Х_і – варіанта або значення ознаки, яка має різне значення в досліджуваній сукупності, n – число варіант (число одиниць сукупності); ∑ – знак суми (сігма велика).

При розрахунку середнього віку засуджених, середнього строку позбавлення волі, середнього навантаження на одного суддю одна і та ж варіанта (Х) може повторюватися декілька разів, декілька десятків разів або навіть тисяч разів, тобто повторюватися з тією чи іншою частотою.

Тому якщо дані представлені згруповано, то до вказаної формули вводиться символ f – частота і розрахунок проводиться за формулою зваженої середньої, загальний вигляд якої такий:

,

де – зважена ступенева середня; Х_і – варіанта усереднюваної ознаки, або середина інтервалу, m – показник ступеня середньої, f_і – частота, яка показує скільки разів зустрічається варіанта.

Отже, можна сказати, що вибір звичайної середньої або зваженої визначається тим статистичним матеріалом, який необхідно проаналізувати.

Правильну характеристику сукупності з варіаційної ознаки у кожному окремому випадку дає тільки один цілком визначений вид середньої. Він зумовлений існуючими зв’язками між середньою та елементами, від яких вона залежить.

Формально середніх є безкінечно багато, але практичне застосування мають не більше десятка з них, які по суті є різним проявом двох: середньої арифметичної, та середньої геометричної.

Крім ступеневих середніх величин, у правовій статистиці застосовуються структурні середні величини, які є описовими характеристиками ряду розподілу ознаки – мода (Мо) і медіана (Me).

3. Ступеневі середні

Залежно від мети дослідження обирається вид ступеневої середньої (арифметичної, геометричної тощо)

	Проста	Зважена
Середня арифметична якщо т = 1			У правовій статистиці широко застосовується для оцінки навантаження слідчих, прокурорів, суддів; обчислення середньої кількості осіб, що припадає на одну кримінальну справу, середнього віку засуджених, середнього строку розгляду справ тощо.
Середня геометрична якщо m = 0			Використовується при розрахунку середньорічних темпів динаміки (приросту) юридично значущих явищ (х1, х2,..., хп – ланцюгові коефіцієнти динаміки)
Середня квадратична якщо т = 2			Середня квадратична величина застосовується при вивченні зв’язків між досліджуваними явищами та їх причинами методом кореляційного аналізу та ін.
Середня гармонійна якщо т = -1			Дуже рідко застосовується у правовій. Це обернена величина середньої арифметичної й обчислюється, якщо є варіанти й добуток варіант на частоти, а частоти відсутні.

Середня арифметична являє собою відношення сумарної величини всіх варіант ознаки до їх чисельності.

Розглянемо розрахунок середньої арифметичної на прикладі:

річне навантаження 8 суддів міського суду, що спеціалізуються на розгляді цивільних справ, становило: 20, 40, 55, 70, 40, 20, 70, 40. Необхідно обчислити середнє річне навантаження на одного суддю. Застосовуємо

.

Розрахунок проведений за середньою арифметичною простою. Вона застосовується, коли дані не згруповані або частоти однакові.

Якщо б ці дані були представлені у такому вигляді:

Таблиця 4

Кількість цивільних справ, х	Кількість суддів, f	то для розрахунку слід було скористатися формулою
20	2	середньої зваженої:
40	3
55	1
70	2
Разом	8

При розрахунку середньої арифметичної часто не обов’язково знати вагу кожного індивідуального значення (варіант). В офіційній статистичній звітності є сумарні розміри. На основі цих узагальнених показників можна обчислити середню арифметичну величину.

В тому ж самому прикладі, знаючи кількість суддів (8) та їх загальне навантаження (20 + 40 + 55 + 70 + 40 + 20 + 70 + 40 = 315) можна розрахувати їх середнє навантаження:

315 : 7 = 45 справ

Ускладнюється розрахунок середньої арифметичної, якщо дані для розрахунку представлені у вигляді інтервального варіаційного ряду. Для цього інтервальний ряд потрібно перетворити у дискретний, тобто визначити середину інтервалу як напівсуму мінімального та максимального значення ознаки у кожній групі. І до формули як Х_і підставляється значення середини кожного інтервалу.

Середня геометрична величина

Деякі явища характеризуються тим, що загальний обсяг ознаки по сукупності визначається не сумою елементів, а їх добутком.

Наприклад, у районі за 1998 рік було зареєстровано 20913 злочинів, а в 2007 р. – 31308 (2007 - 1998 = 9). Середньорічний темп зростання зареєстрованих злочинів становив:

тобто з 1998 по 2007 р. злочинність щорічно збільшувалася на 4,6 %.

Якщо відомі темпи динаміки за кожний рік, то розраховується середній темп зростання за весь період за формулою

де х₁, х₂, ..., х_п – ланцюгові темпи динаміки; п – кількість ланцюгових темпів динаміки.

Наприклад, кількість зареєстрованих злочинів у місті збільшилася:

у 2002 р.	на 13,1 %, або в	1,131 рази;
у 2003 р.	на 12%, або в	1,12 рази;
у 2004 р.	на 11,5 %, або в	1,115 рази;
у 2005 р.	на 1 1 %, або в	1,11 рази;
у 2006 р.	на 12%, або в	1,12 рази;
у 2007 р.	на -14,4 %, або в	0,856 рази.

Середній річний темп динаміки зростання за ці роки становить:

Якщо маємо темпи динаміки явища за певний відомий період, то розрахунок роблять за першою формулою.

Припустімо, з 1993 по 2002 р. злочинність у місті зросла в 1,5 раза. Отже, середньорічний темп зростання злочинності можна обчислити так: