МИНИСТЕРСТВО ПУТЕЙ СООБЩЕНИЯ РОССИИ

ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПУТЕЙ СООБЩЕНИЯ

Кафедра “ Автоматика и телемеханика на железных дорогах ”

СИНТЕЗ АСИНХРОННЫХ

И СИНХРОННЫХ АВТОМАТОВ

Задание на контрольную работу

и методические указания по дисциплине

“ Теория дискретных устройств железнодорожной автоматики,

телемеханики и связи на железнодорожном транспорте”

САНКТ-ПЕТЕРБУРГ

1998

Данные методические указания являются продолжением методических указаний по дисциплине “Теория дискретных устройств железнодорожной автоматики, телемеханики и связи” для студентов III курса специальности “Автоматика, телемеханика и связь на железных дорогах”. Они предназначены для выполнения контрольной работы по данной дисциплине и содержат две части:

• Часть 3 – синтез асинхронных конечных автоматов;

• Часть 4 – синтез синхронных автоматов.

Выбор номера варианта задания определяется аналогично первой части работы, а таблицы вариантов приведены в конце каждой части.

3. Синтез асинхронных конечных автоматов

Цель практического задания – изучение и применение на практическом примере метода синтеза асинхронного конечного автомата с помощью кодирования состояний по столбцам таблицы переходов. Метод исключает критические состязания элементов памяти.

3. 1. Основные положения

Асинхронные конечные автоматы относятся к классу многотактных устройств. Многотактное устройство отличается от комбинационного тем, что при одинаковых воздействиях на входе и на выходе могут быть разные сигналы или их последовательности. Для реализации этого свойства многотактное устройство должно обладать памятью, т. е. способностью запоминать последовательности входных сигналов.

В

Рис. 3.1.

дискретных автоматах запоминание осуществляется с помощью цепей обратной связи (ОС) или спе-циальными элементами памяти (ЭП). Цепь ОС (рис. 3.1.) соединяет выход ком-бинационной схемы (КС) с одномерным входом. Особенностью такой памяти является то, что сигнал на выходе y комбинационной схемы в статическом состоянии

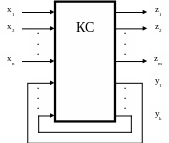
зависит от этого же сигнала на ее входе. На рисунке 3. 1. введены следующие обозначения:

x₁,…, x_n- сигналы на входах устройства ( входные переменные);

y₁,…, y_k- сигналы в цепях ОС ( внутренние переменные) ;

z₁,…, z_m- сигналы на входе устройства.

Для примера рассмотрим многотактную схему, реализованную на релейно – контактных элементах (рис. 3. 2). ОС в схемах на релейно – контактных элементах организуется введением в цепи включения реле Y_i его собственного контакта y_i. Такую цепь принято называть цепью самоблокировки.

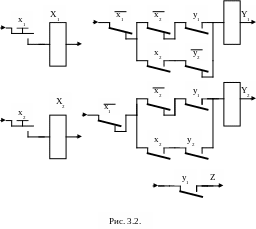
Пусть в исходном состоянии кнопки не нажаты (x₁=x₂=0) и реле выключены (Y₁=Y₂=0) .После нажатия кнопки x₂ включается реле Y₁ и своим контактом y₁ подготавливает цепь самоблокировки. После нажатия кнопки x₂ включается реле Y₁ и своим контактом y₁ подготавливает цепь самоблокировки. Кроме того, на выходе Z появится сигнал (Z=1). После отпускания кнопки x₂ на входах схемы устанавливается исходное значение входных сигналов x₁=x₂=0. Однако реле Y₁ остается включенным по цепи самоблокировки и выходной сигнал Z₁=1. Таким образом, наличие в схеме ОС дало возможность запомнить факт нажатия кнопки.

Из приведенного примера видно, что для описания работы многотактной схемы недостаточно знать значения входных и выходных сигналов, но необходимо знать значение сигналов на входе элементов памяти (в цепях ОС). Совокупность состояний петель ОС (элементов памяти, внутренних реле) называют внутренним состоянием многотактной схемы. Общее число внутренних состояний при k цепях ОС равно 2^k. Совокупность состояний ОС и входных сигналов называют полным состоянием схемы.

Многотактные устройства делятся на два класса: синхронные и асинхронные.

Работа синхронного автомата зависит от специальных сигналов, поступающих от независимого источника синхронизации, что обусловливает его надежную работу. В отличие от синхронного в асинхронном автомате все изменения обусловливаются изменением сигнала на входе.

Следовательно, длительность входного воздействия должна быть такой, чтобы обеспечивалось надежное изменение внутреннего состояния автомата. Переход от такта к такту происходит либо за счет изменения входного воздействия, либо за счет изменения внутреннего состояния автомата. Обычно принимают, что переход от такта к такту происходит мгновенно, т. е. время реагирования всех элементов памяти является одинаковым (однотактный переход). В общем случае в течение изменяемого входного сигнала автомат может несколько раз изменить свое внутреннее состояние (многотактный переход).

В синхронном автомате различают два вида тактов – устойчивый и неустойчивый.

Устойчивым называется такт работы автомата, в котором не создается условий для изменения его внутреннего состояния. Длительность такого такта определяется моментами изменения входного воздействия.

Неустойчивым называется такт, в котором создаются условия для изменения внутреннего состояния автомата. Длительность такого такта определяется временем реагирования элементов памяти. В связи с этим говорят, что в неустойчивом такте автомат находится в неустойчивом состоянии, а в устойчивом такте – в устойчивом состоянии.

Наиболее распространенным способом задания асинхронного конечного автомата (АКА) является таблица переходов (ТП) и таблица выходов (ТВ).

В качестве примера представлены ТП (табл.3.1) и ТВ (табл.3.2). Столбцы обеих таблиц соответствуют различным состояниям входа автомата, строки – внутренним состояниям автомата.

Таблица 3.1 Таблица 3.2

S x		x2	x1	x1 x2		S x		x2	x1	x1 x2
1	(1)	2	(5)	(6)		1	0	0	0	0
2	3	(2)	5	6		2	1	0	0	0
3	(3)	2	5	6		3	1	1	0	0
4	1	2	5	6		4	0	1	0	0

Таблица 3.3

S x		x2	x1	x1 x2
1	(1), 0	2	(5), 0	(6), 0
2	3	(2), 0	5	6
3	(3), 1	4	5	6
4	1	(4), 1	5	6

На пересечении i-й строки и j-го столбца ТП указывает то внутреннее состояние, в которое автомат перейдет из внутреннего состояния s_i (i-я строка) под действием входных сигналов,соответствующих состоянию входа X (j-й столбец).Устойчивые состояния в ТП отмечаются круглыми скобками. На пересечении i-й строки и j-го столбца ТВ указывается то состояние Z, которое будет иметь место, если на автомат, находящийся в состоянии s_i, поступает входной сигнал x_j.

На практике часто эти две таблицы совмещают в одну (табл. 3. 3). В этом случае в клетке, где проставлено устойчивое состояние, проставляется и значение выхода.

Один из важнейших этапов синтеза АКА, реализующего заданную ТП, состоит в том, чтобы представить внутренние состояния в виде комбинаций значений внутренних переменных . Эта процедура называется кодированием внутренних состояний АКА. Рассмотрим процедуру кодирования для ТП (см. табл. 3. 1).

ТП содержит 4 состояния, поэтому потребуется две внутренние переменные y₁ и y₂ (два ЭП), так как из двух переменных можно получить 2ⁿ= 4 комбинаций: 00, 01, 10, 11.

В общем случае n элементов памяти имеют 2ⁿ состояний. Если ТП имеет r строк, то минимально необходимое число внутренних переменных определяется по формуле:

q = ] log 2 r [ .

где P=> r ближайшее к r число, которое является степенью числа 2 (P=2^q => r).

Кодирование состояний заключается в присвоении каждой строке ТП одной из комбинаций (двоичных наборов) внутренних переменных. Пусть внутреннему состоянию 1 состветствует двоичный набор 00 (y₁=y₂=0), внутреннему состоянию 2 – 01, 3 - 10, 4 – 11. Затем строится кодированная ТП. Для этого цифра в каждой клетке ТП заменяется двоичным набором соответствующей строки (табл. 3. 4).

Таблица 3. 4

S x	y1 y2		x2	x1	x1 x2
1	0 0	(0 0)	0 1	(0 0)	(0 0)
2	0 1	1 0	(0 1)	0 0	0 0
3	1 0	(1 0)	1 1	0 0	0 0
4	1 1	0 0	(1 1)	0 0	0 0

Например, в клетках на пересечении строк 1 и 4 со столбцом проставлен код 00, который соответствует внутреннему состоянию 1, а в строках 2 и 3 проставлен код 10, соответствующий состоянию 3. Кодированная ТП дает возможность определить поведение АКА при смене входных сигналов и переходе его из одного состояния в другое.

Рассмотрим клетку ТП с координатами ( x₂, 01). В ней записано состояние 01. Это означает, что при наличии на входе сигнала 01 реле Y₁ должно остаться в выключенном состоянии, а реле Y₂ во включенном, т. е. состояние ЭП сохраняется, что соответствует устойчивому состоянию 2 схемы. Чтобы осуществить переход из состояния 2 в состояние 3, необходимо изменить значение входных сигиалов на 00. В клетке с координатами (00, 01) записано состояние 10. Это означает, что если реле Y₁ было без тока, а реле Y₂ – под током и на вход поступил сигнал 00, то реле Y₁ должно включиться, а реле Y₂ – выключиться. Следовательно в данной клетке поставлено состояние 3, которое является неустойчивым.

Особенность рассматриваемого перехода из состояния 2 в состояние 3 заключается в том, что одновременно происходит изменение состояния обоих реле. Поэтому работа схемы оказывается в зависимости от временных параметров этих реле.

В данном примере возможны 2 случая.

1.Y₁ включается раньше, чем выключается реле Y₂. В этом случае схема окажется в состоянии 4 (Y₁=Y₂=1), а затем выключается Y₂ и схема переходит в состояние 3.

2.Y₁ выключается раньше, чем выключится реле Y₂. В этом случае схема окажется в состоянии 1 (Y₁=Y₂=0). Но это полное состояние (00, 00) является устойчивым, и для реле Y₂ здесь записано условие его выключения. По этой причине Y₂ не выключается и схема останется в состоянии 1, вместо того, чтобы перейти в состояние 3.

Явленияе, когда возникают условия для изменения состояния одновременно двух или более реле, называется состязанием реле. Если в результате состязаний реле не происходит нарушения заданного алгоритма работы схемы, то такие состязания называются некритическими.

Например в случае 1 схема все равно переходит в состояние 3, как и определено алгоритмом. Если в результате состязаний реле происходит нарушение заданного алгоритма работы схемы, то такие состязания называются критическими. Например, в случае 2 схема вместо состояния 3 перешла в состояние 1, следовательно, имеют место критические состязания реле.

Для того, чтобы АКА выполнял заданный алгоритм работы, критические состязания элементов памяти в нем должны быть исключены.