ЗМІСТ

Практична робота №1. Визначення похибок при комп’ютерному моделюванні……………………………….	4
Практична робота №2. Приклади обчислень елементарних функцій з використанням рядів Тейлора. Визначення похибок обчислень…………………………….	9
Практична робота №3. Інтерполяція і наближення функцій за допомогою методу Лагранжа, поліномів Ньютона і Чебишева…………………………………………	14
Практична робота №4. Машинний розв'язок систем лінійних алгебраїчних рівнянь……………………………...	22
Практична робота №5. Машинний розв'язок нелінійних рівнянь…………………………………………...	32
Практична робота №6. Чисельний розв'язок диференціальних рівнянь методами Ейлера, Гюна і Рунне-Кутта…………………………………………………..	38
Практична робота №7. Чисельний розв'язок систем диференціальних рівнянь……………………………………	49
Практична робота №8. Чисельний розв'язок гіперболічних рівнянь……………………………………….	53
Практична робота №9. Чисельний розв'язок параболічних та еліптичних рівнянь………………………..	59
Перелік рекомендованих джерел………………………	73

Практична робота №1

Визначення похибок при комп’ютерному моделюванні

1.1 Мета роботи

1 Вивчення джерел і класифікація похибок, що виникають при розв'язку на ЕОМ наукових та інженерних задач.

2 Вивчення правил наближених обчислень і оцінка похибок.

3 Оцінка з використанням ЕОМ абсолютної і відносної похибок функцій багатьох змінних.

1.2 Короткі теоретичні відомості

Одержуваний за допомогою ЕОМ результат y майже завжди, за рідкісним винятком, містить похибку, тобто є наближеним.

Основні джерела і класифікація похибок математичного моделювання:

а) математична модель є наближеним описом реальної наукової, інженерної або іншої практичної задачі;

б) вихідні дані містять похибки, внаслідок того, що вони отримані в результаті вимірювань або інших розрахунків;

в) математичні методи у більшості випадків є наближеними;

г) через обмеженість розрядності обчислювальної машини і використовуваних способів представлення чисел в ЕОМ при введенні і виведенні, а також при виконанні арифметичних операцій здійснюється заокруглення.

Величина похибки _н – що виникає внаслідок перших двох причин називається неусувною похибкою. Похибка _м джерелом якої є метод називається похибкою методу. Обчислювальною похибкою називається похибка _у, що виникає при введенні, виводі і виконанні арифметичних операцій на ЕОМ.

Максимальна відносна похибка заокруглення називається машинним епсилон _ і визначається розрядністю ЕОМ.

Абсолютна і відносна похибки

Нехай a - точне значення деякої величини, а^* - відоме наближене значення цієї величини. Додатна величина називається абсолютною похибкою величини a. Відношення абсолютної похибки величини а до її абсолютного значення називається відносною похибкою.

. (1.1)

Максимальне значення (а) називається граничною абсолютною похибкою і позначається (а). Відповідно гранична відносна похибка дорівнює:

. (1.2)

Іноді слово “ гранична” не зазначають і під абсолютною і відносною мають на увазі абсолютну і відносну граничні похибки. Нижче слово “граничне“ також не буде повторюватися.

Похибки арифметичних операцій

а) при додаванні і відніманні двох величин їхні абсолютні похибки додаються:

. (1.3)

б) при множенні і діленні двох величин їхні відносні похибки визначаються:

, (1.4)

. (1.5)

в) при піднесені у степінь наближеної величини її відносна похибка збільшується на показник степеня:

. (1.6)

Похибка функцій

Нехай а - наближене значення аргументу x функції y=f(x), а а- абсолютна похибка, тобто При а<<1 для оцінки абсолютної похибки і відносної похибок використовуються наступні вирази:

. (1.7)

Аналогічні співвідношення можна записати для функції декількох змінних, наприклад, якщо U=f(x,y,z), то при:

маємо:

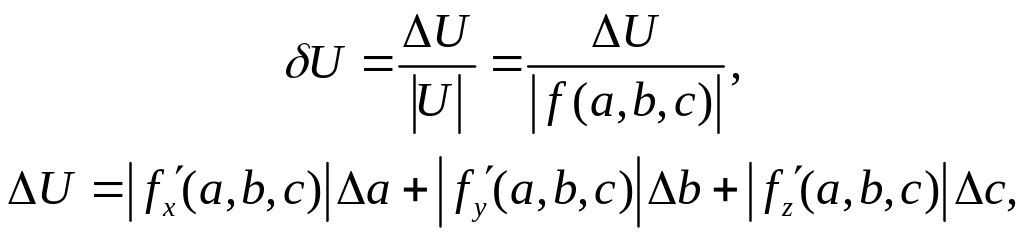(1.8)

де частинні похідні за відповідними аргументами.

Визначення машинного епсилон

При виконанні операції додаванні двох чисел 1+ при <<1 внаслідок заокруглення буде отримане результуюче число 1. Оскільки точне значення суми повинно дорівнювати 1+, а одержуване значення дорівнює 1, то абсолютна похибка суми (1+) дорівнює . Так як за означенням машинне епсилон _ є відносною похибкою округлення , то маємо

.

Таким чином, якщо визначити таке значення  при якому 1+ = 1, то це значення буде дорівнює _.

З цією метою в циклі досить організувати обчислення послідовності: _n+1=_n/2, n=0,1,..., починаючи з ₀=1 і перевірку виконання умови 1+_n+1=1. При деякому n умова 1+_n+1=1 буде виконана, звідси і визначається значення _=_n+1.