Задания для самостоятельного решения
|
|
|
a)
|
|
|
|
a) , b) , c) . |
|
|
|
a)
,
b)
|
|
|
|
a)
,
b)
|
|
|
|
a)
,
b)
|
|
|
|
a)
,
b)
|
|
|
|
a)
,
b)
|
|
|
|
a) , b) , c) . |
|
|
|
a)
,
b)
|
|
|
|
a) , b) , c) . |
|
|
|
a) , b) , c) . |
|
|
|
a) , b) , c) . |
|
|
|
a) , b) , c) . |
|
|
|
a) , b) , c) . |
|
|
|
a) , b) , c) . |
|
|
|
a) , b) , c) . |
|
|
|
a) , b) , c) . |
|
|
|
a) , b) , c) . |
|
|
|
a) , b) , c) . |
|
|
|
a) , b) , c) . |
|
|
|
a) , b) , c) . |
|
|
|
a) , b) , c) . |
|
|
|
a) , b) , c) . |
|
|
|
a) , b) , c) . |
|
|
|
a) , b) , c) . |
|
|
|
a) , b) , c) . |
|
|
|
a) , b) , c) . |
|
|
|
a) , b) , c) . |
|
|
|
a) , b) , c) . |
|
|
|
a) , b) , c) . |
;
,
b)
,
c)
.
;
;
,
c)
.
;
,
c)
.
;
,
c)
.
;
,
c)
.
;
,
c)
.
;
;
,
c)
.
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
Задача 2
Вычислить пределы.
Решение.
а)
;
б)
;
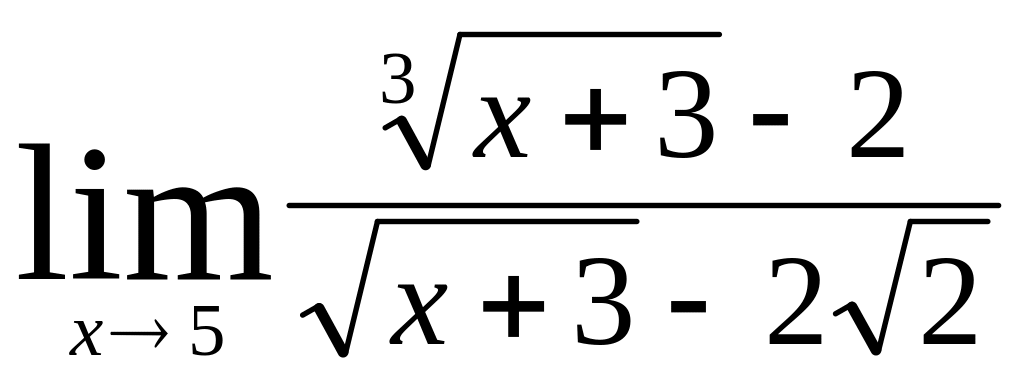в)
.
а) .
При непосредственной подстановке получаем неопределенность:
.
Для того,
чтобы избавиться от данного вида
неопределенности, домножим числитель
и знаменатель дроби, стоящей под знаком
предела на величины, сопряженные
числителю и знаменателю (т.е. на
и
):
.
б) .
При непосредственной подстановке получаем неопределенность:
.
Для того,
чтобы избавиться от данного вида
неопределенности, введем новую переменную
,
где
(т.е
есть наименьшее общее кратное показателей
радикалов, стоящих в числителе и в
знаменателе). В нашем случае
.
Кроме того,
следовательно
,
или
.
Таким образом, мы получаем
.
Однако,
непосредственная подстановка опять
приводит к неопределенности
,
которую мы устраним, разложив числитель
и знаменатель дроби на множители,
используя формулы сокращенного умножения:
.
в) .
При непосредственной подстановке получаем неопределенность:
.
Для того,
чтобы избавиться от данного вида
неопределенности, домножим и разделим
выражение, стоящее под знаком предела
на величину, ему сопряженную (т.е. на
):
.
Однако,
непосредственная подстановка опять
приводит к неопределенности
,
которую мы устраним, разделив числитель
и знаменатель дроби на
:
.
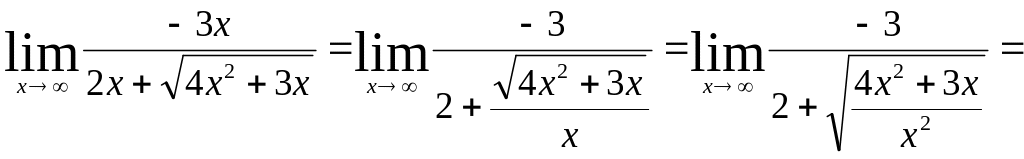
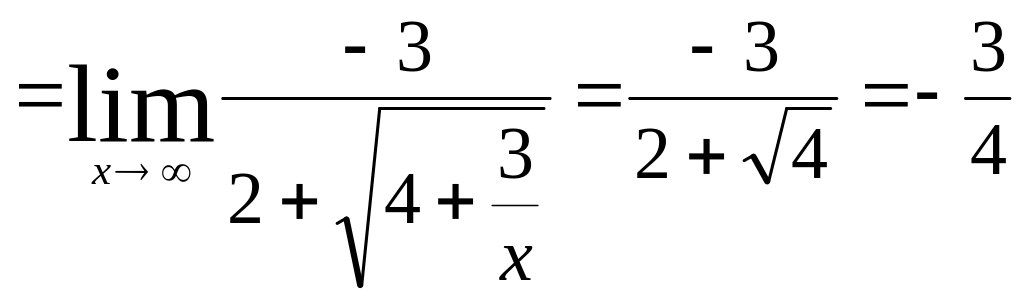