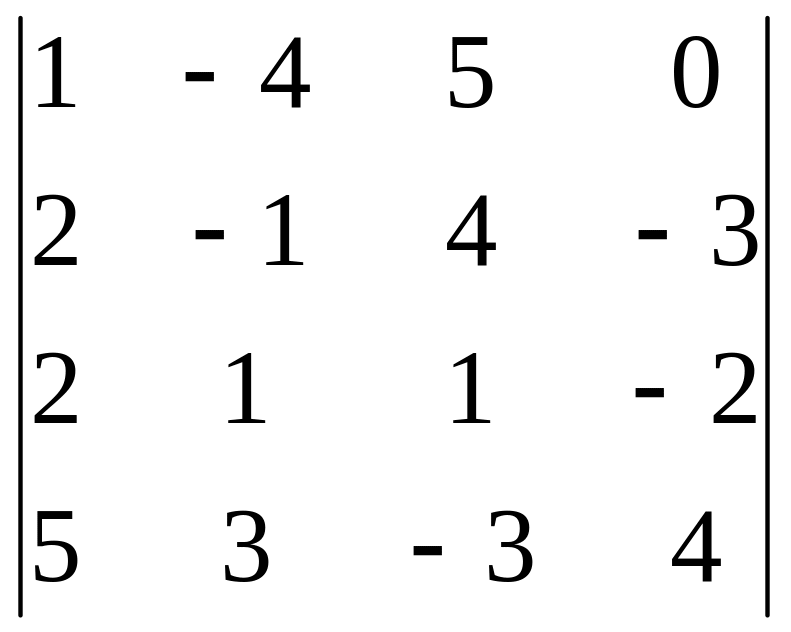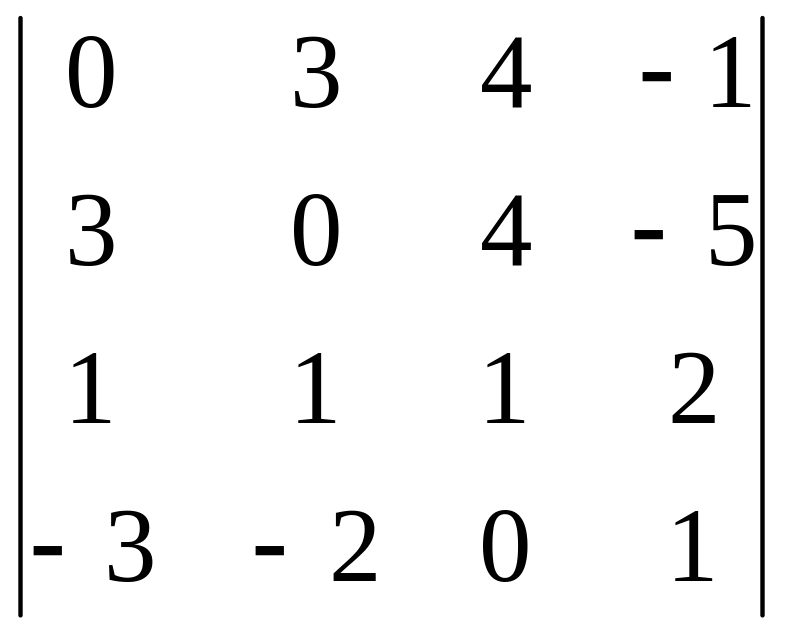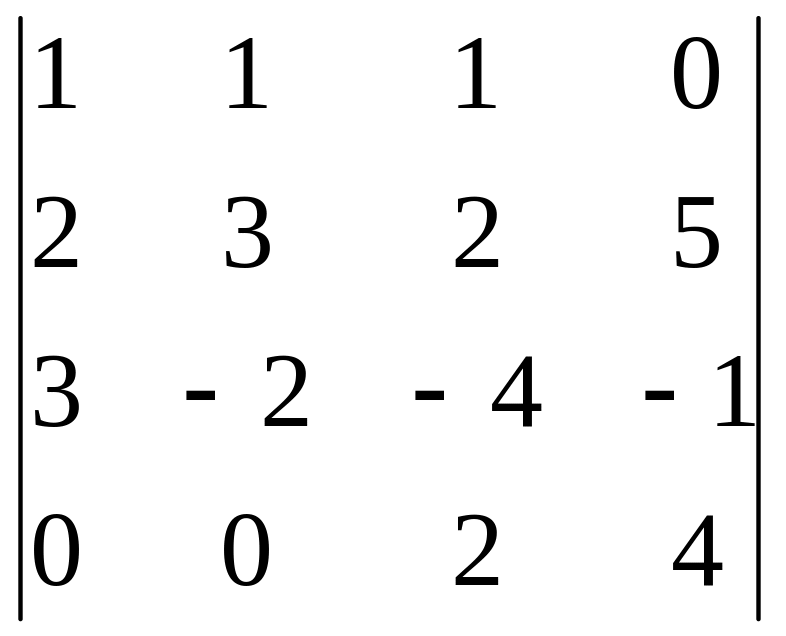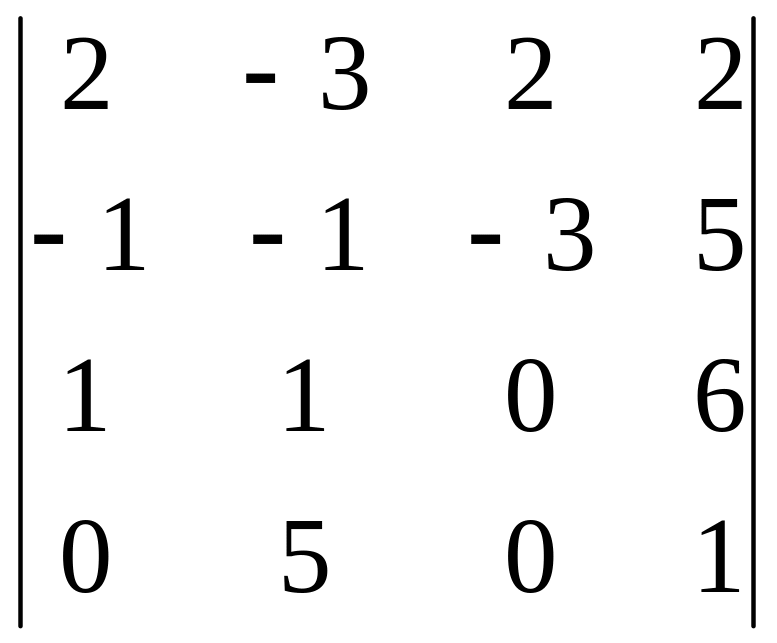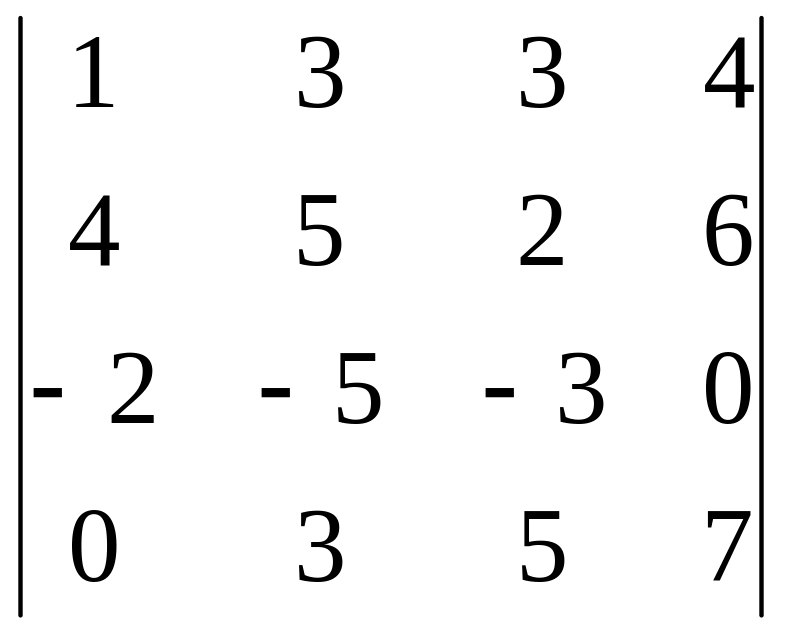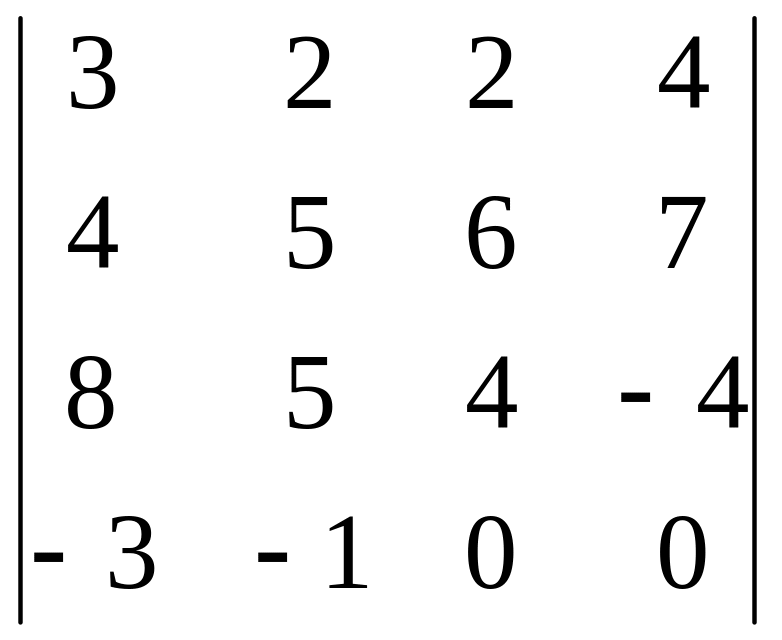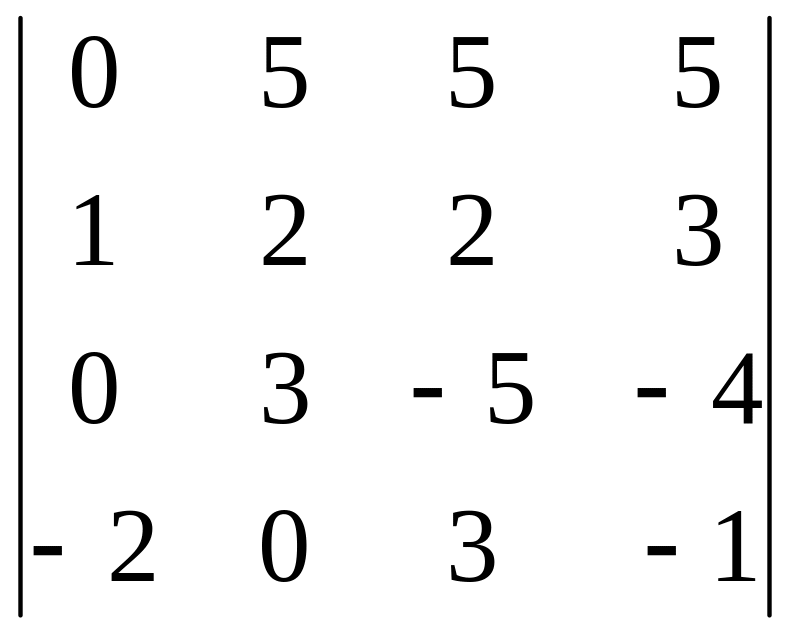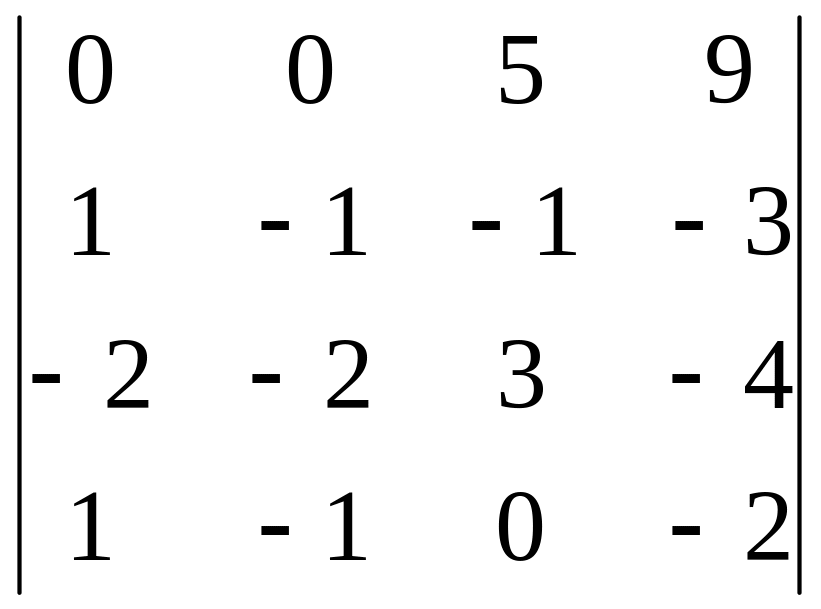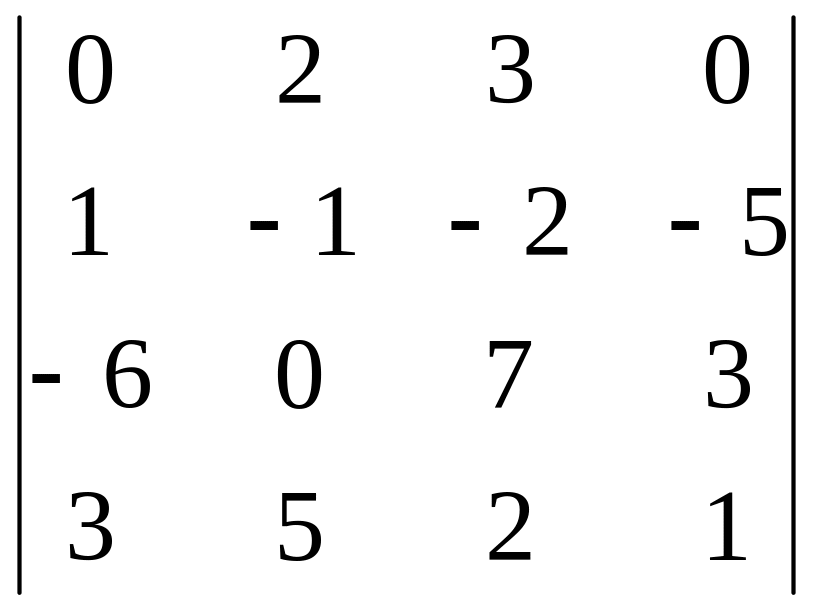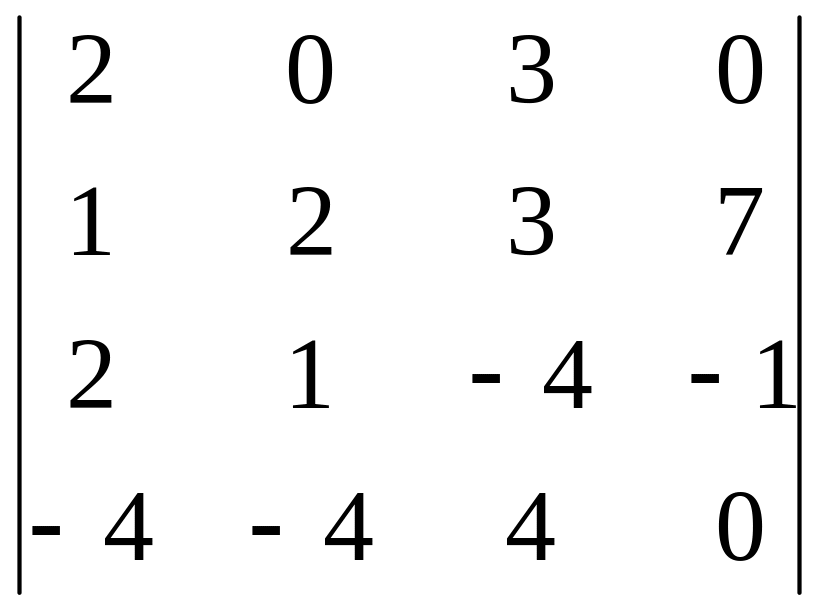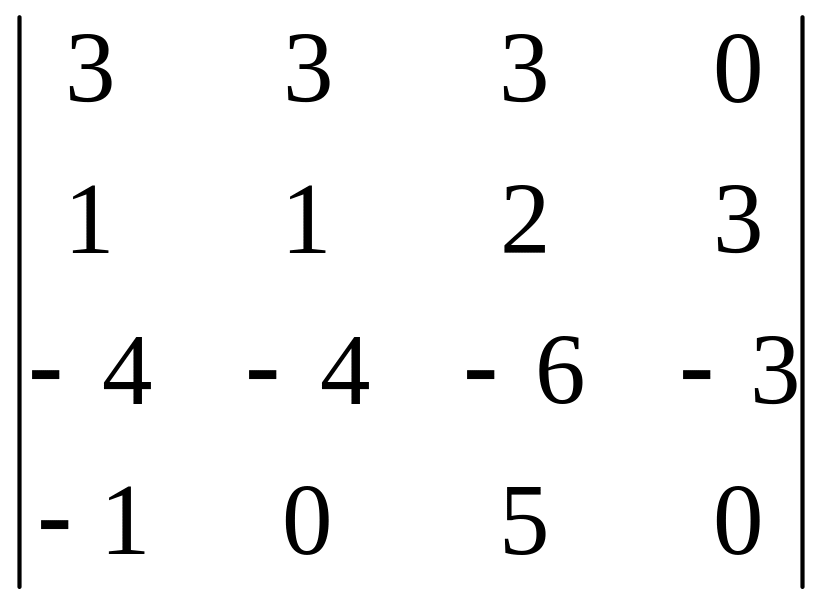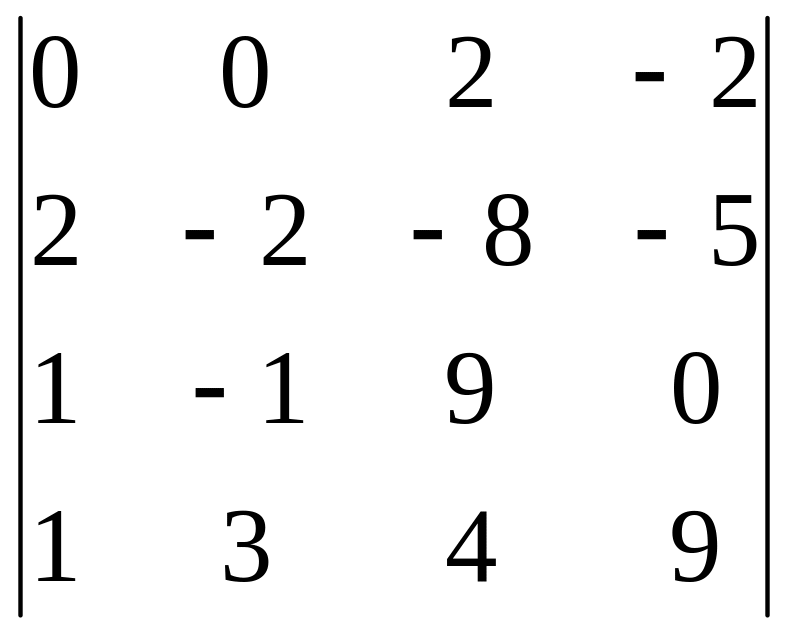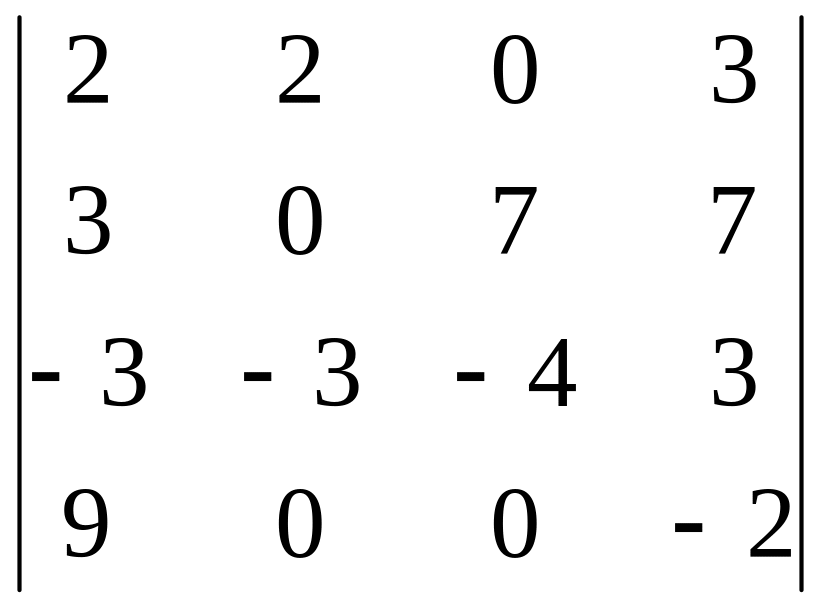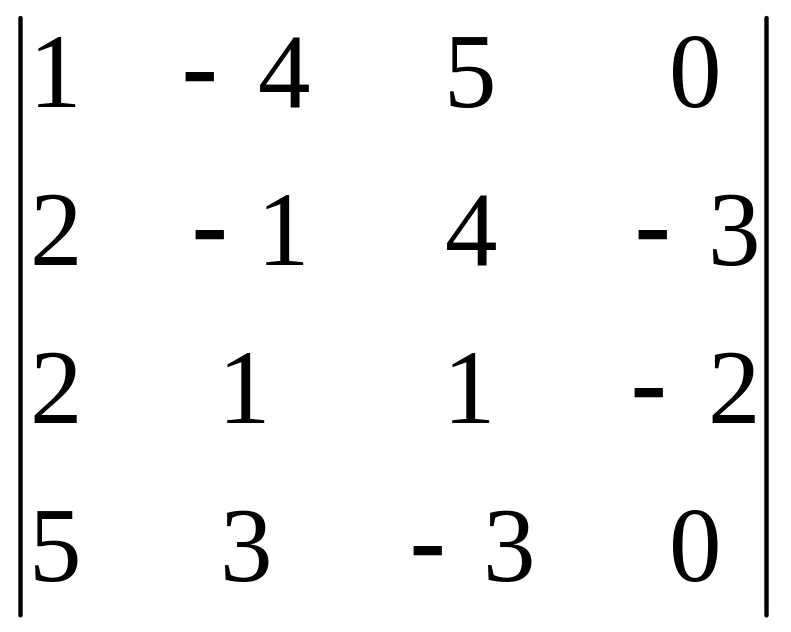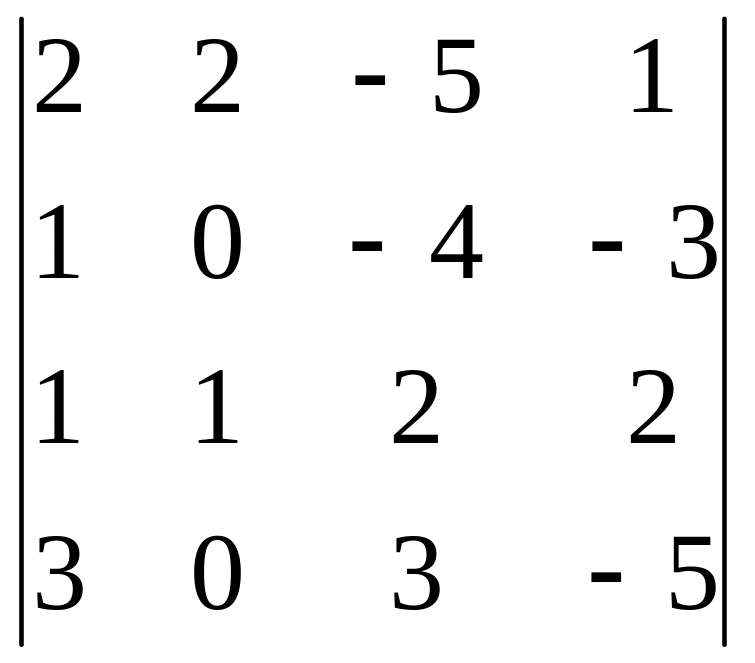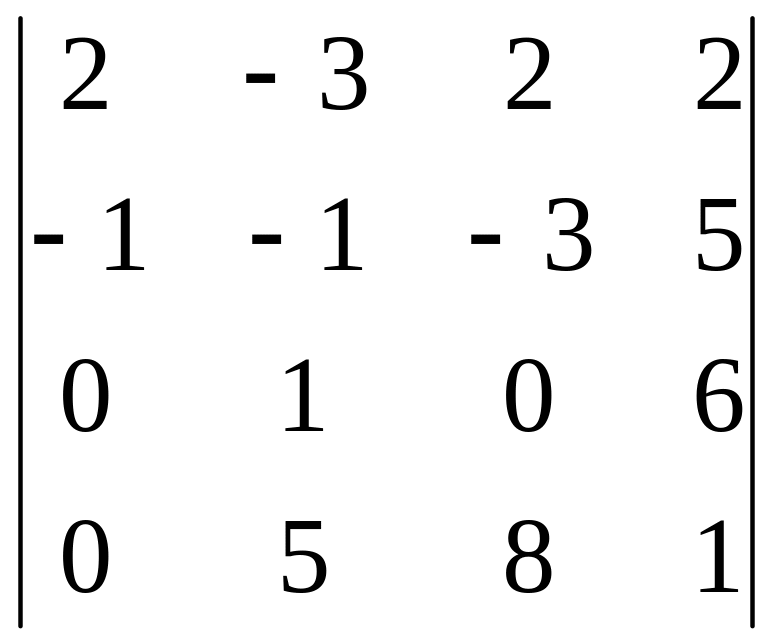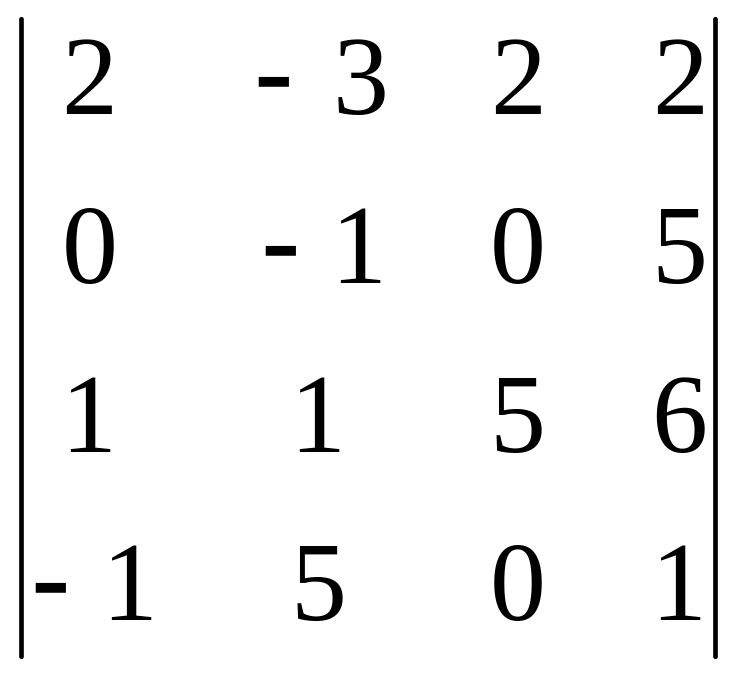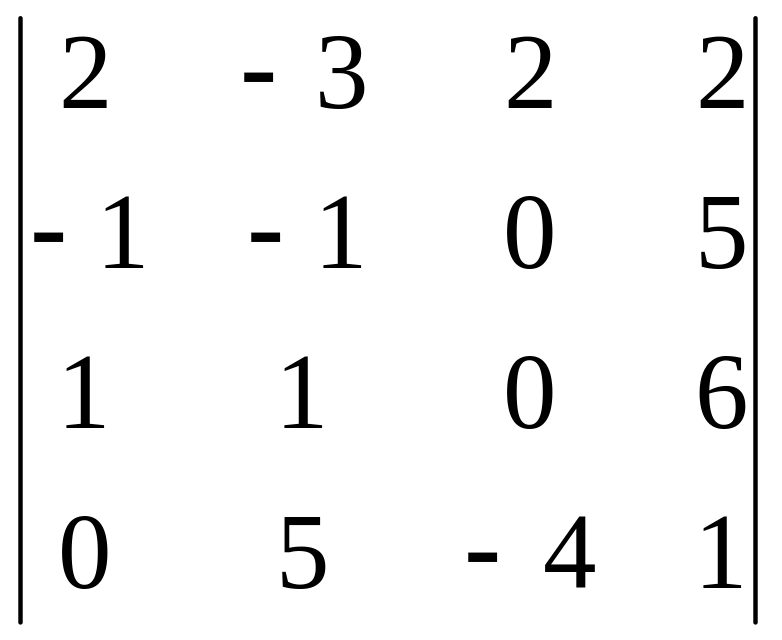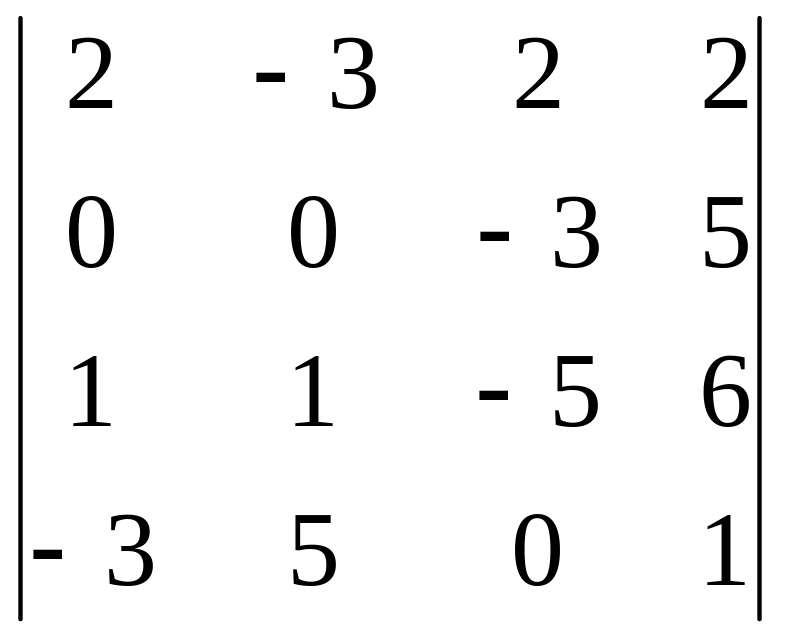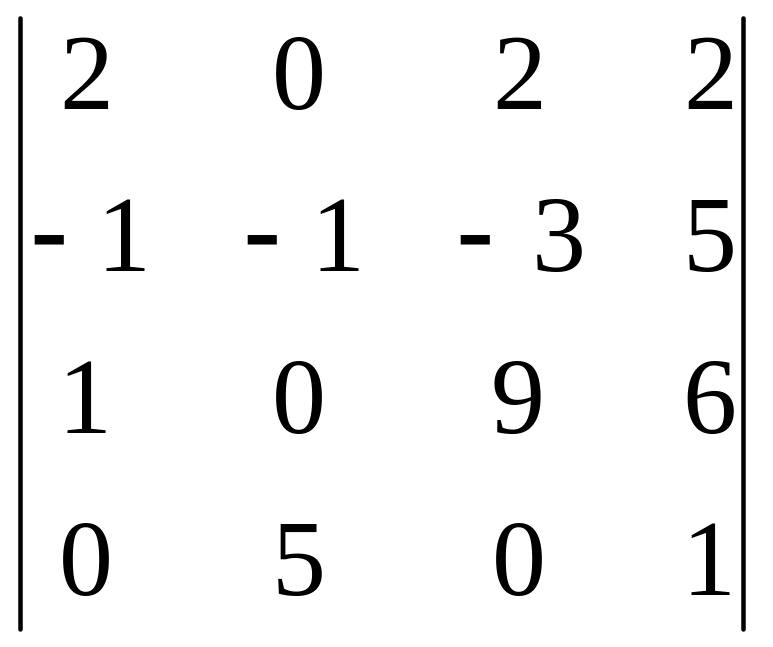- •Министерство сельского хозяйства российской федерации
- •Методические рекомендации к выполнению расчетно – графических работ студентов I курса
- •Введение
- •1 Тема «Линейная и векторная алгебра» Вопросы, выносимые на самостоятельную работу
- •Группа а Задача 1
- •Задания для самостоятельного решения
- •Задача 2
- •Задания для самостоятельного решения
- •Задача 3
- •Задания для самостоятельного решения
- •Задача 4
- •Задания для самостоятельного решения
- •Группа в Задача 1
- •Задания для самостоятельного решения
- •Задача 2
- •Задача 3
- •Задания для самостоятельного решения
- •2. Тема «Аналитическая геометрия» Вопросы, выносимые на самостоятельную работу
- •Задания для самостоятельного решения
- •Задача 3
- •Задания для самостоятельного решения
- •Группа в Задача 1
- •Задания для самостоятельного решения
- •Задача 2.
- •Задания для самостоятельного решения
- •3 Тема «Пределы и производные» Вопросы, выносимые на самостоятельную работу
- •Группа а Задача 1
- •Задания для самостоятельного решения
- •Задача 2
- •Задания для самостоятельного решения
- •Задача 3
- •Задания для самостоятельного решения
- •Группа в Задача 1
- •Задания для самостоятельного решения
- •Задача 2
- •Задания для самостоятельного решения
- •Задача 3
- •Задания для самостоятельного решения
- •Задача 4
- •Задания для самостоятельного решения
- •4 Тема «Приложение производной. Комплексные числа» Вопросы, выносимые на самостоятельную работу
- •Группа а Задача 1
- •Задания для самостоятельного решения
- •Задача 2
- •Задания для самостоятельного решения
- •Задача 3
- •Задания для самостоятельного решения
- •Задача 4
- •Задания для самостоятельного решения
- •Задача 5
- •Задания для самостоятельного решения
- •Группа в. Задача1
- •Задания для самостоятельного решения
- •Задача 2
- •5 Тема «неопределенный и определенный интеграл» Вопросы, выносимые на самостоятельную работу
- •Группа а Задача 1
- •Задания для самостоятельного решения
- •Задача 2
- •Задания для самостоятельного решения
- •Задача 3
- •Задания для самостоятельного решения
- •Задача 4
- •Задания для самостоятельного решения
- •Группа в Задача 1
- •Задания для самостоятельного решения
- •Задача 2
- •Задания для самостоятельного решения
- •Задача 3
- •Задания для самостоятельного решения
Задача 3
Коллинеарны
ли векторы
![]() и
и
![]() построенные
по векторам
построенные
по векторам
![]() и
и
![]() ?
?
![]() .
.![]() и
и
![]()
Решение. По свойствам векторного
произведения, два вектора коллинеарны
тогда и только тогда, когда их векторное
произведение равно нулю. Найдем координаты
векторов
![]() и
и
![]() .
.
![]()
![]()
![]() .
.
![]()
![]()
![]() .
.
Таким образом
![]() ,
,
![]() .
Тогда
.
Тогда
![]()
![]() .
.
Таким образом
![]() ,
следовательно, вектора
и
не коллинеарны.
,
следовательно, вектора
и
не коллинеарны.
Задания для самостоятельного решения
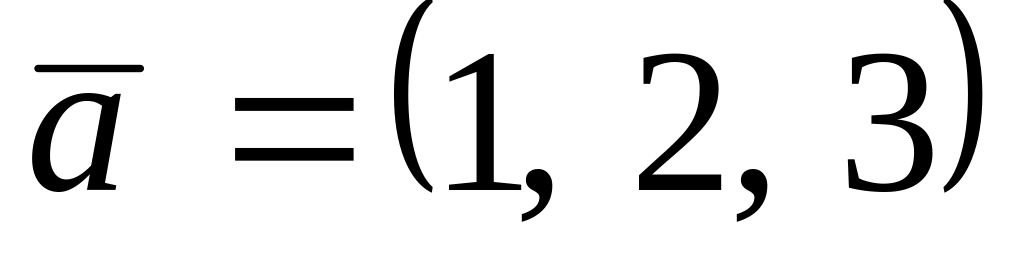 ,
,
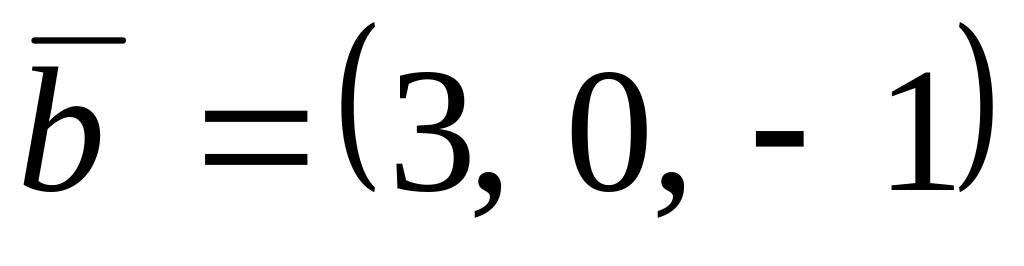 ,
,
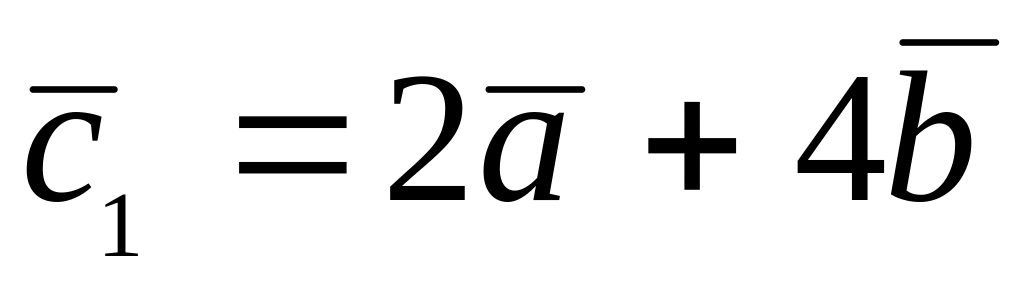 ,
,
 .
.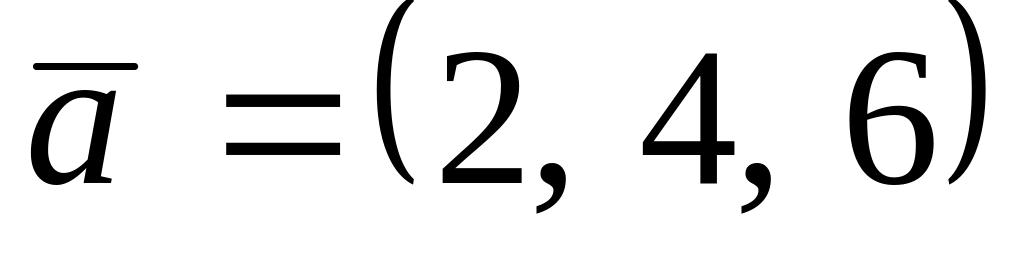 ,
,
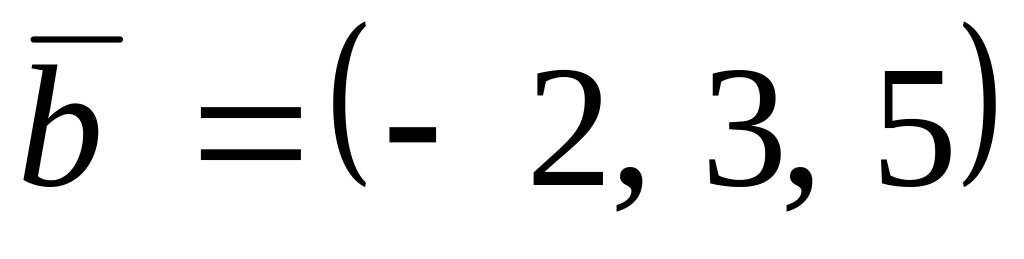 ,
,
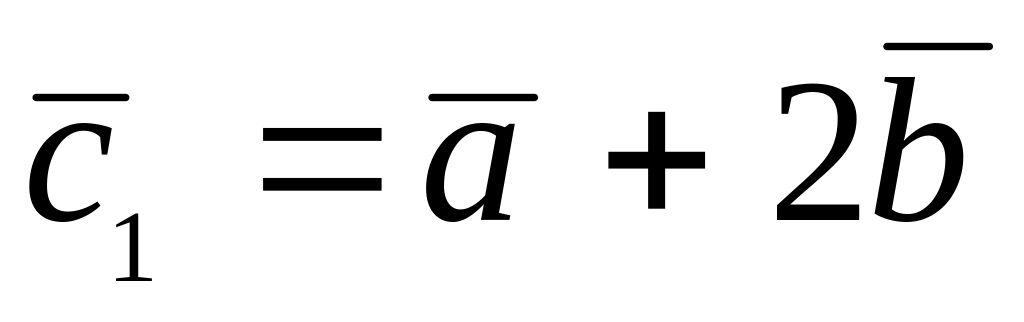 ,
,
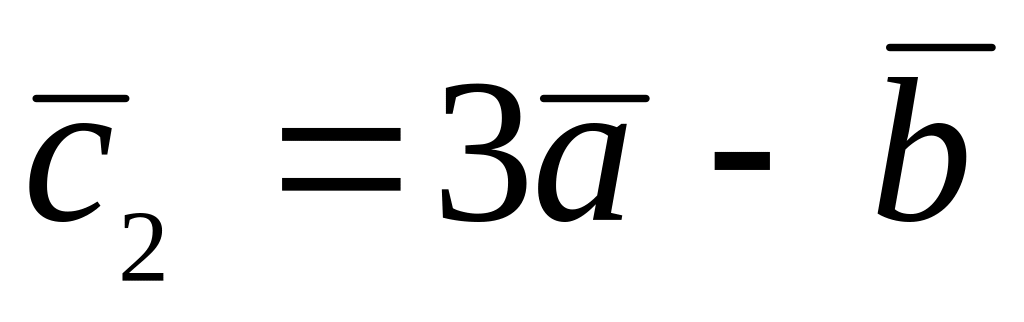 .
.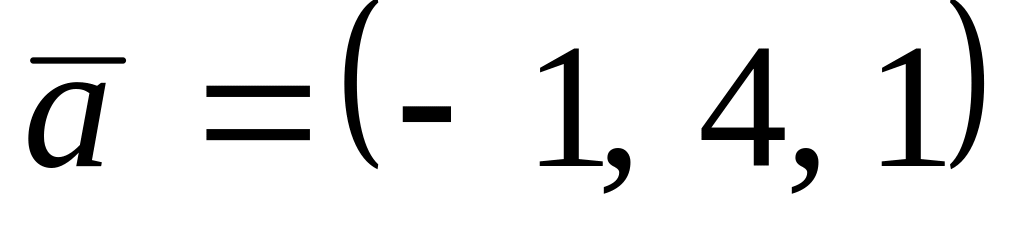 ,
,
 ,
,
 ,
,
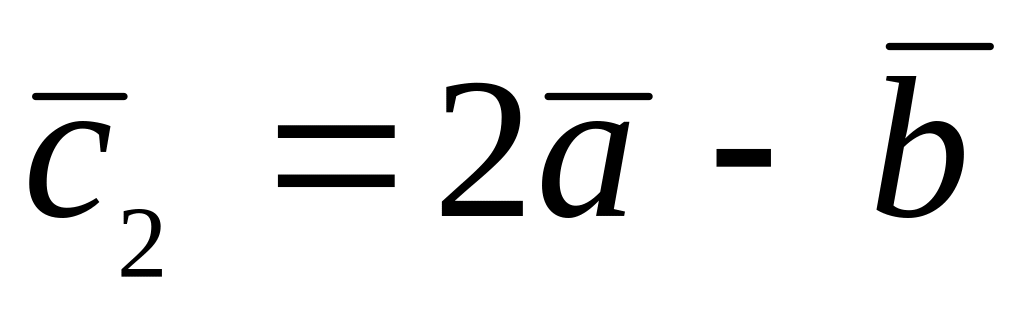 .
. ,
,
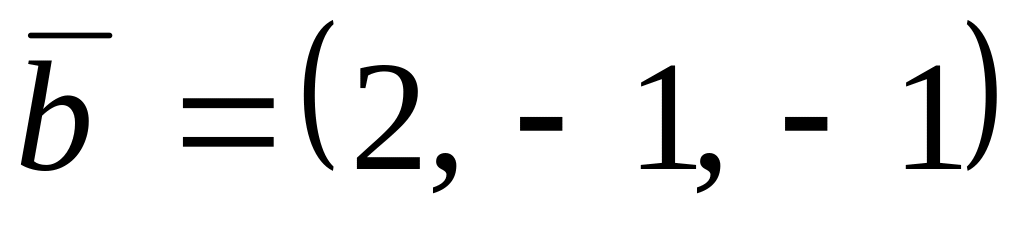 ,
,
 ,
,
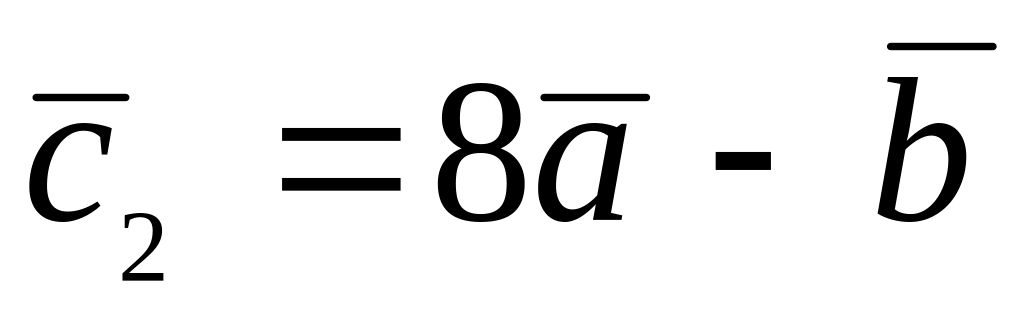 .
.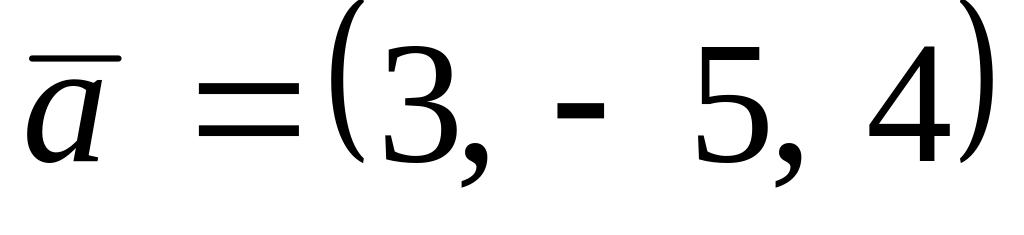 ,
,
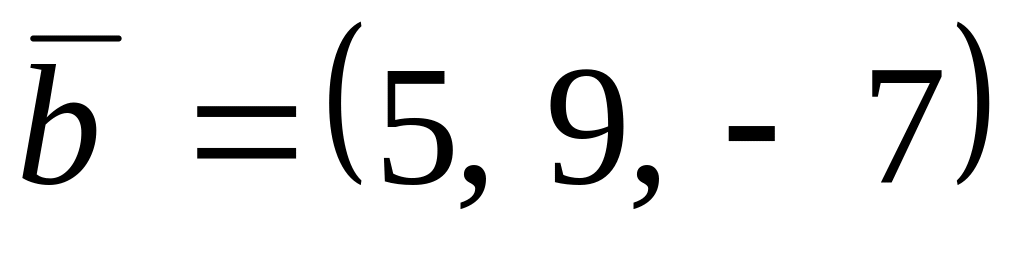 ,
,
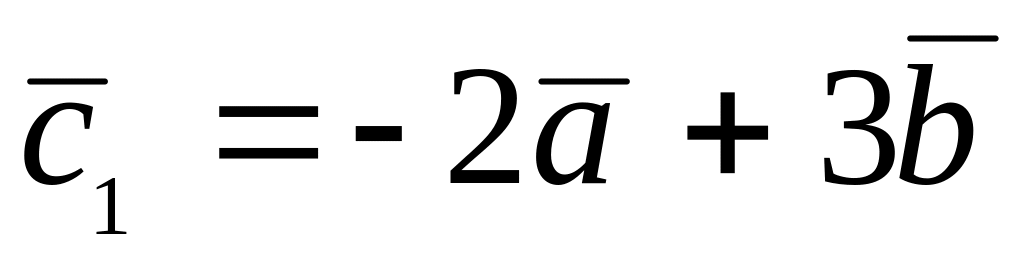 ,
,
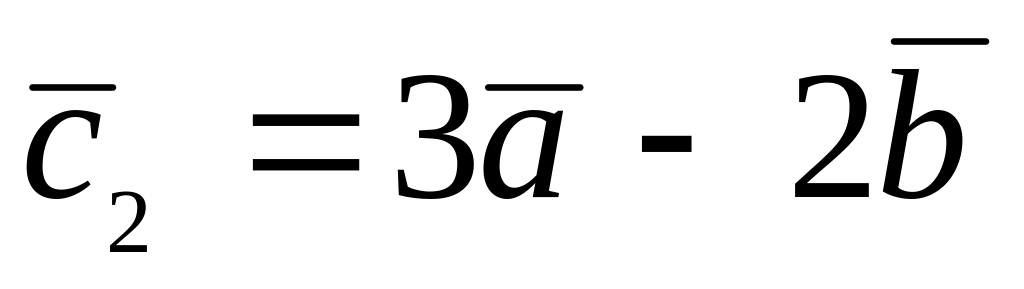 .
. ,
,
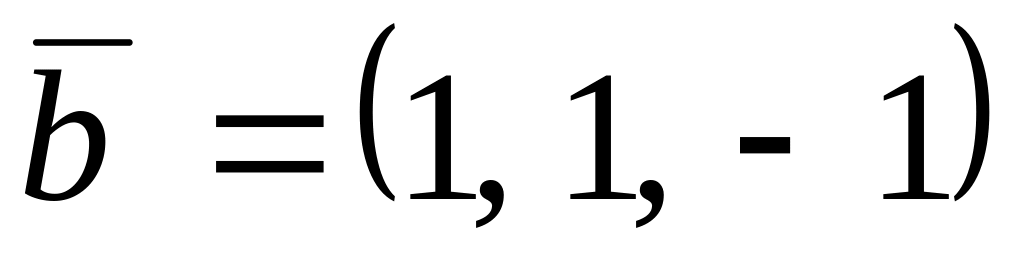 ,
,
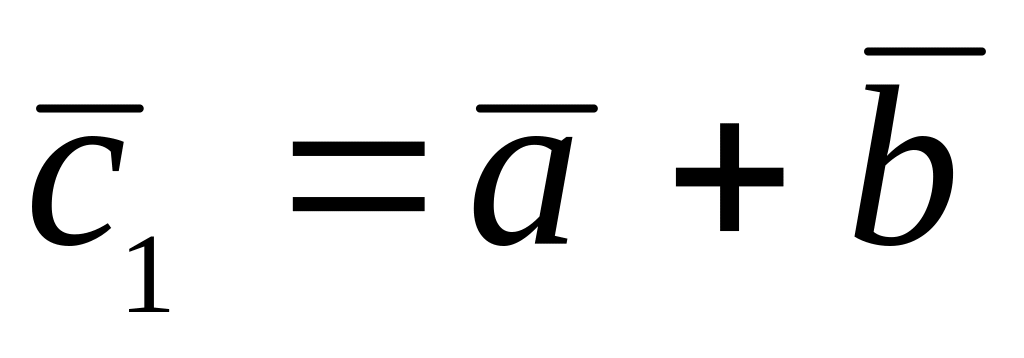 ,
,
 .
.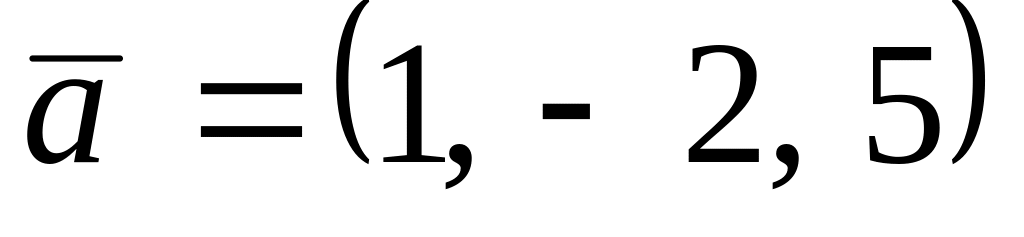 ,
,
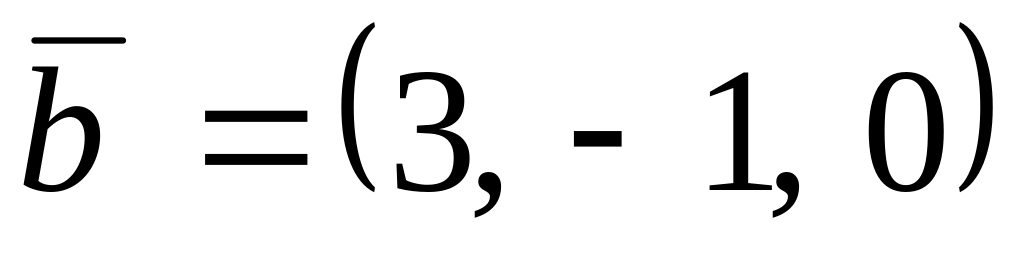 ,
,
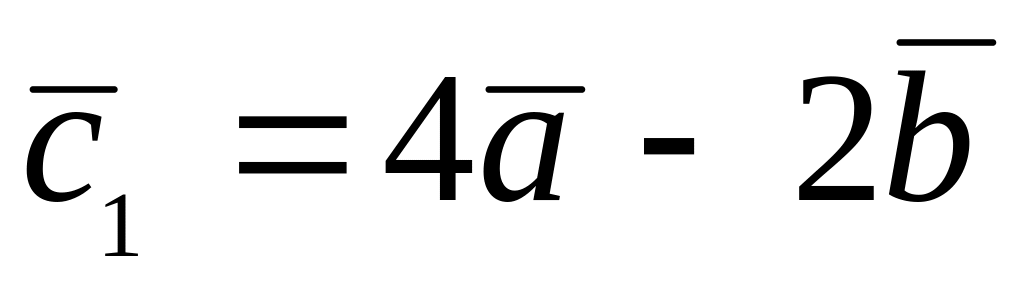 ,
,
 .
.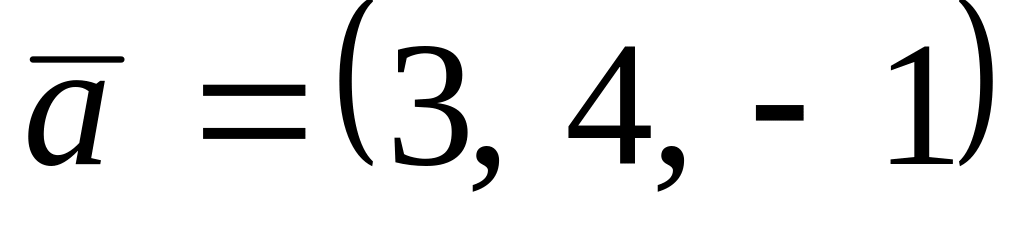 ,
,
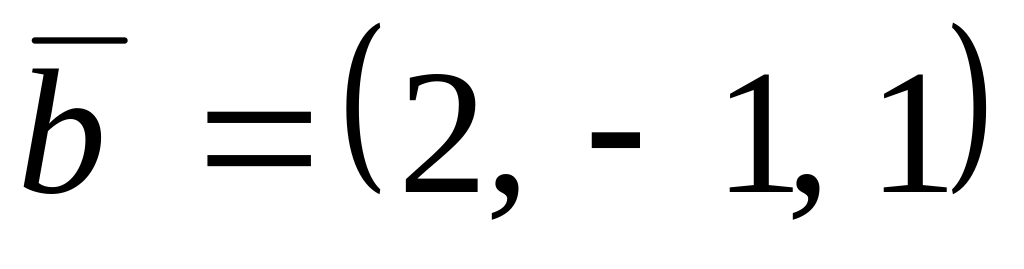 ,
,
 ,
.
,
.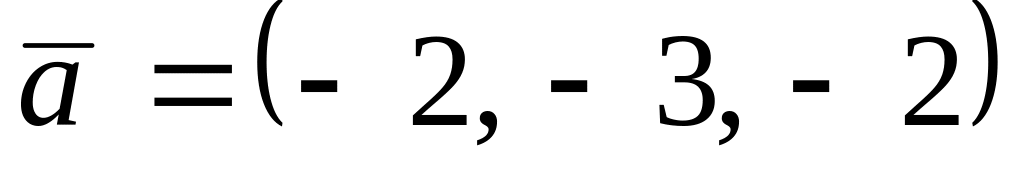 ,
,
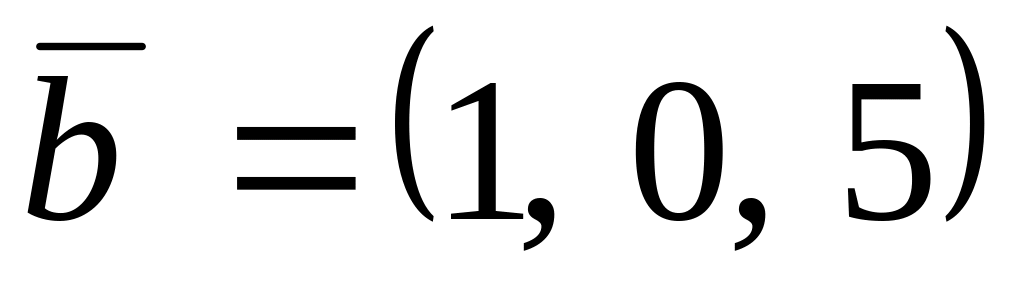 ,
,
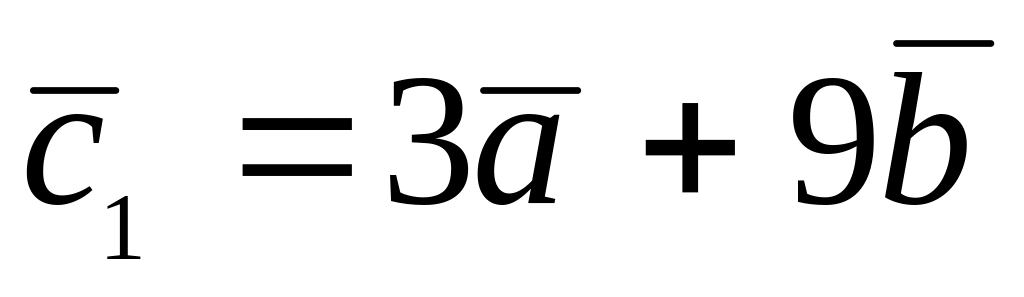 ,
,
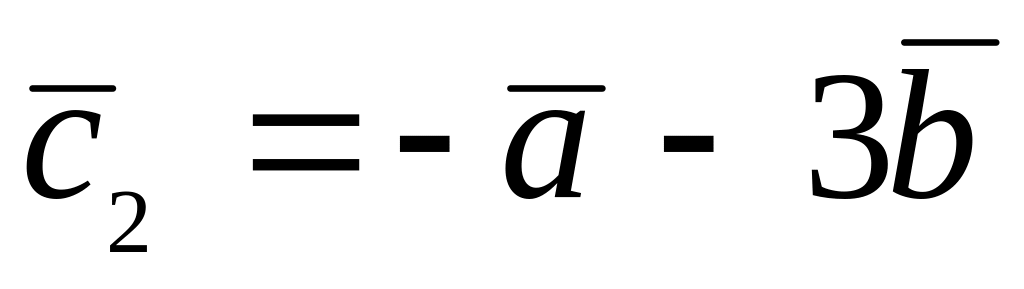 .
.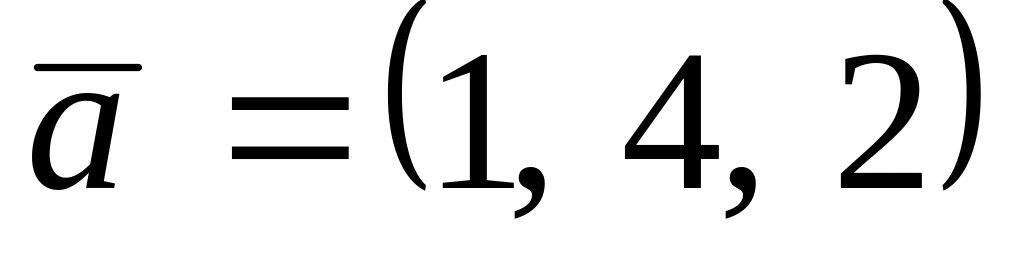 ,
,
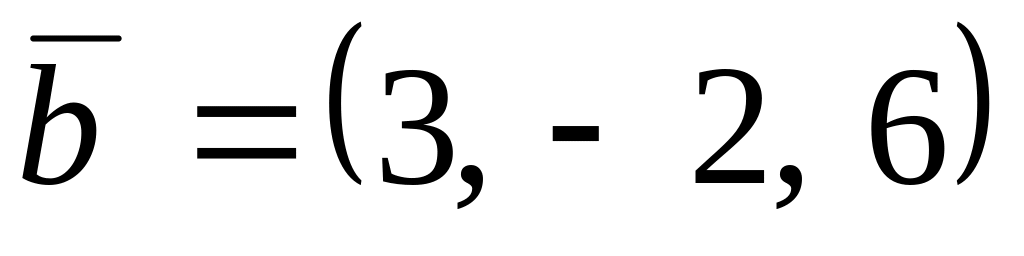 ,
,
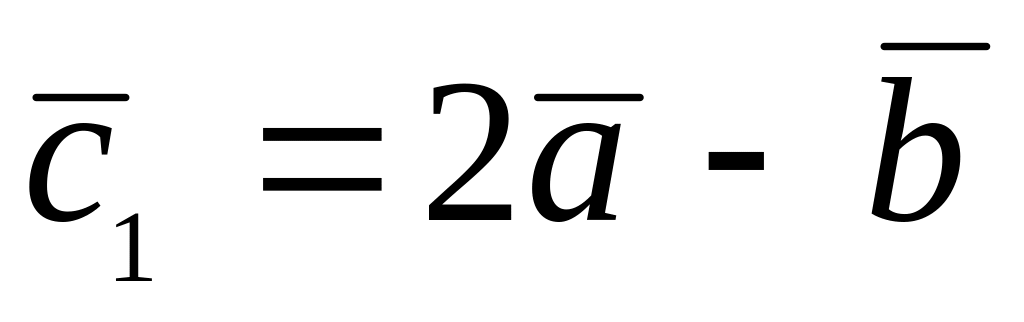 ,
,
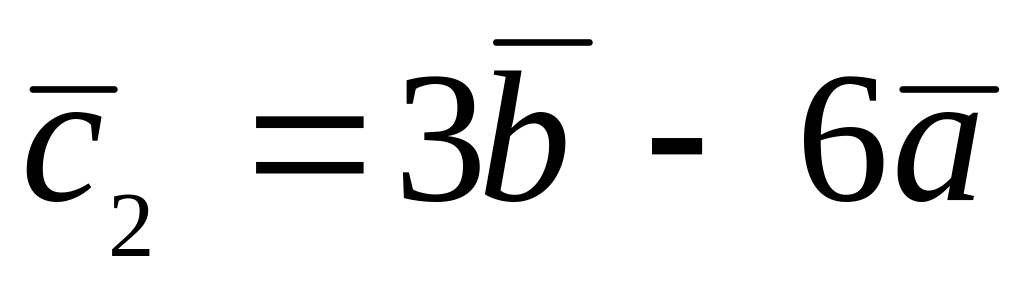 .
. ,
,
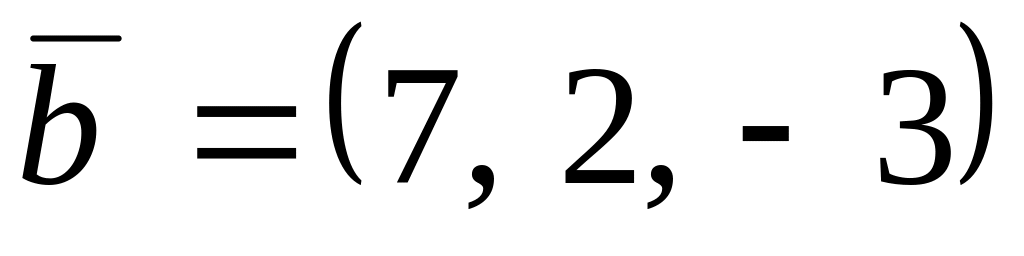 ,
,
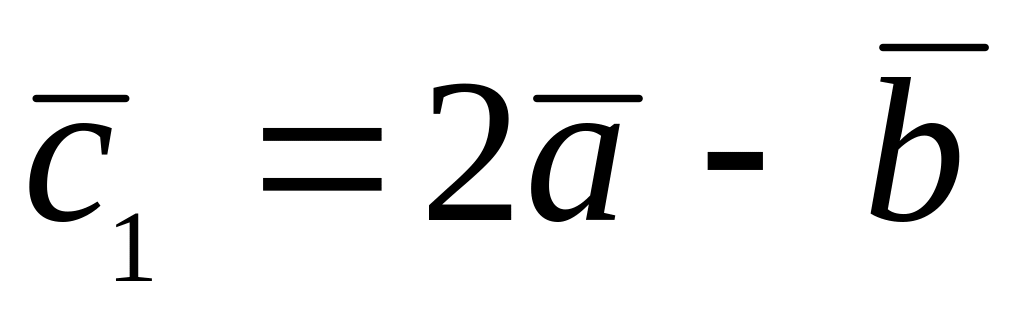 ,
.
,
.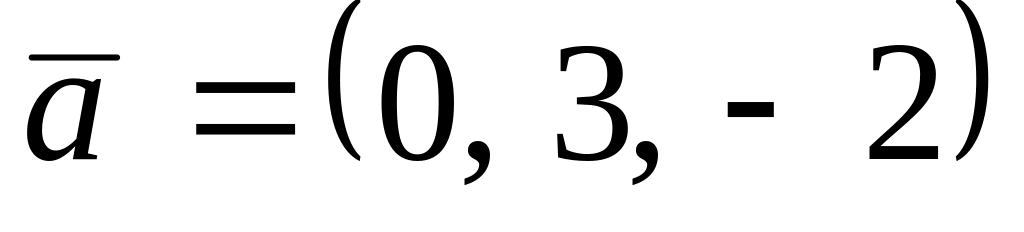 ,
,
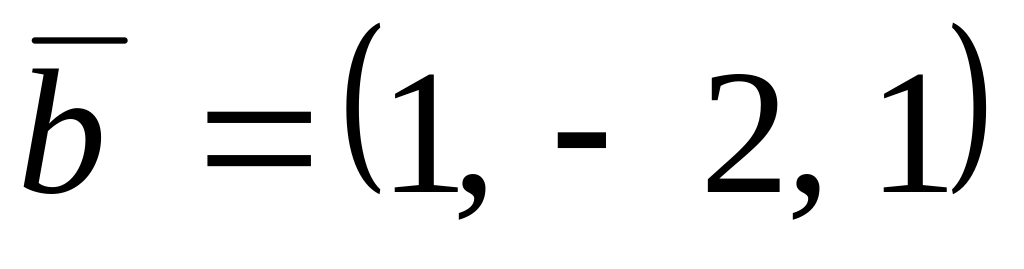 ,
,
 ,
,
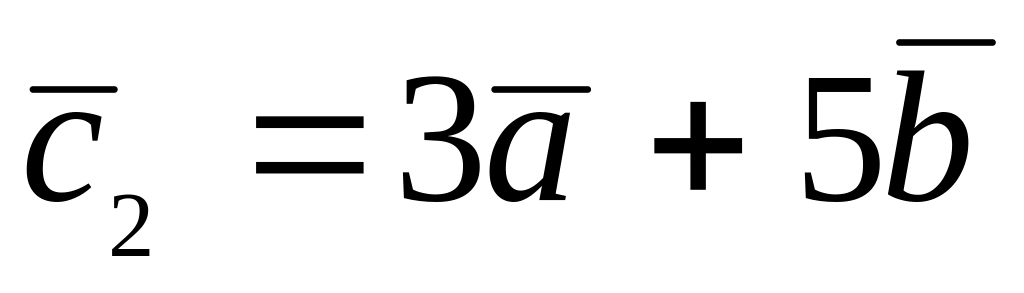 .
.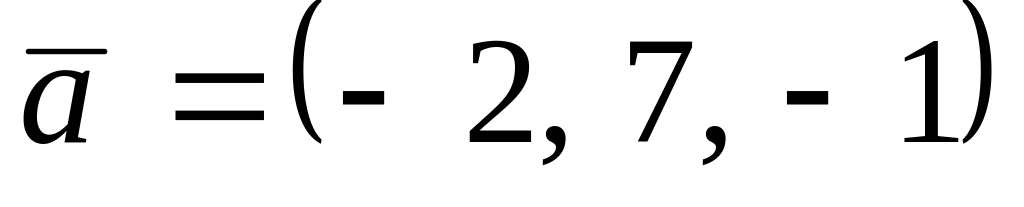 ,
,
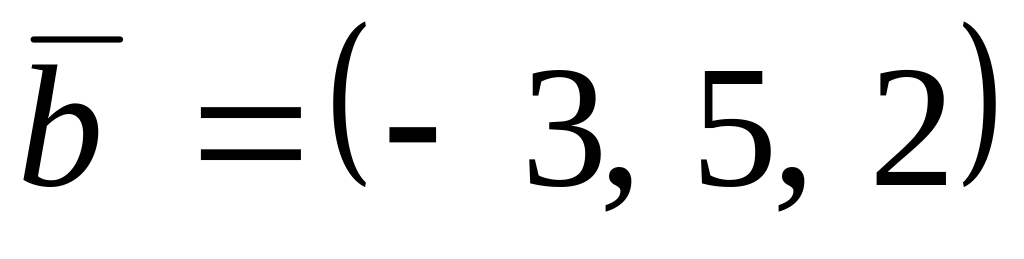 ,
,
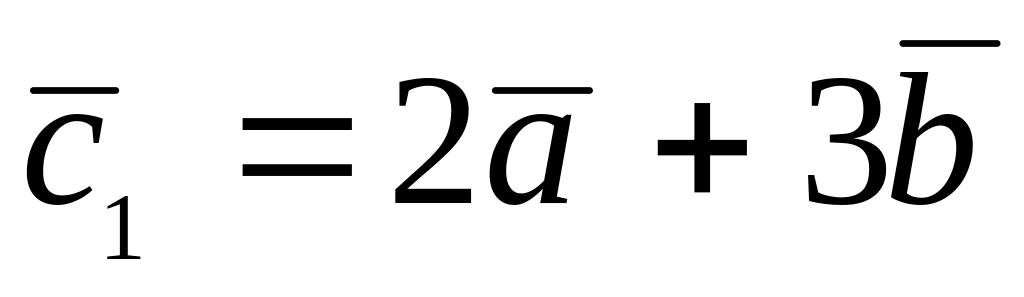 ,
,
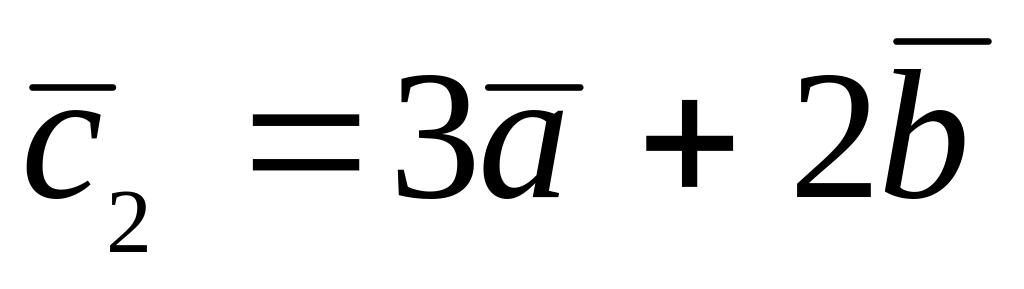 .
.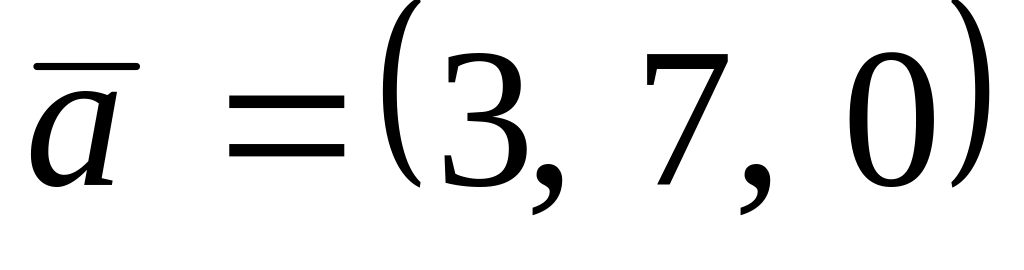 ,
,
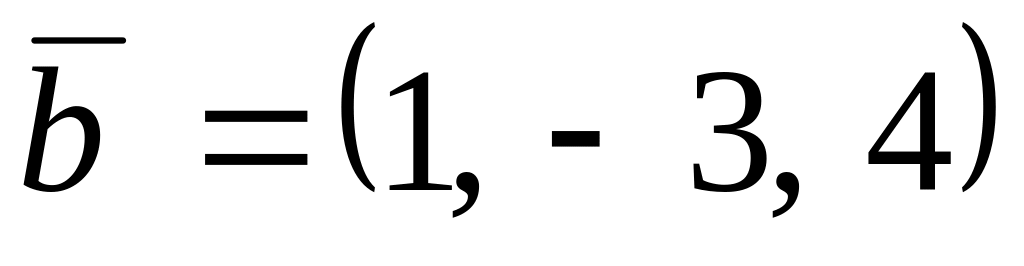 ,
,
.
,
,
.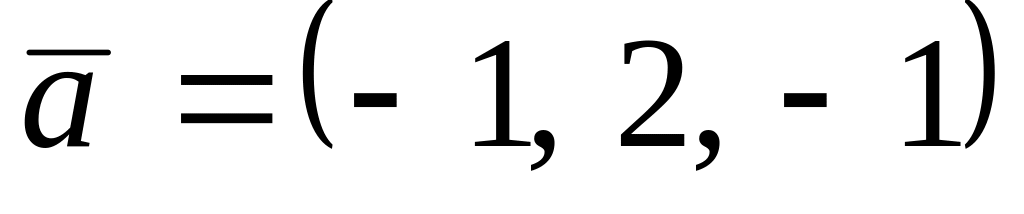 ,
,
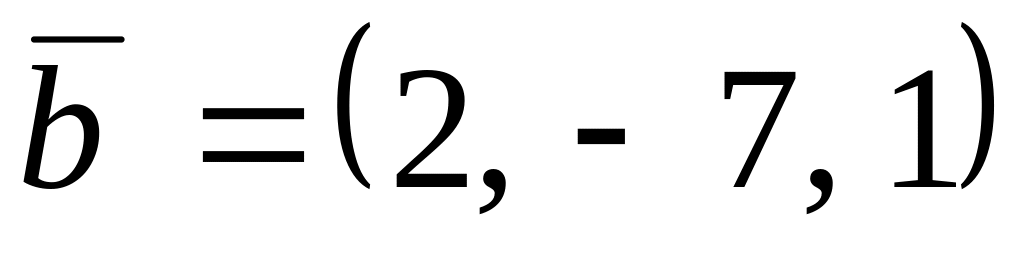 ,
,
 ,
,
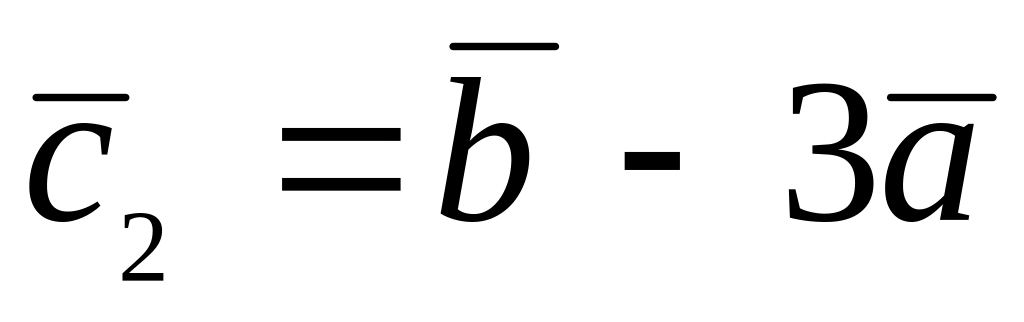 .
. ,
,
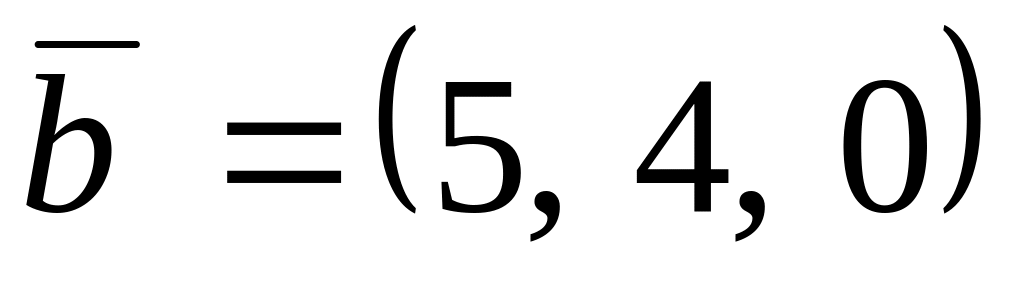 ,
,
 ,
,
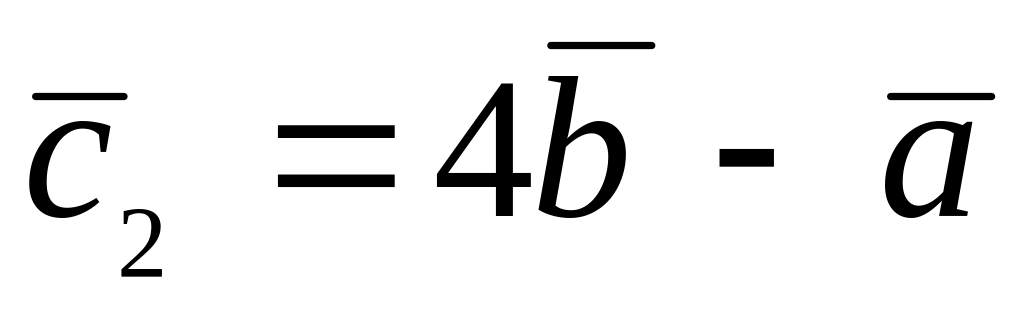 .
.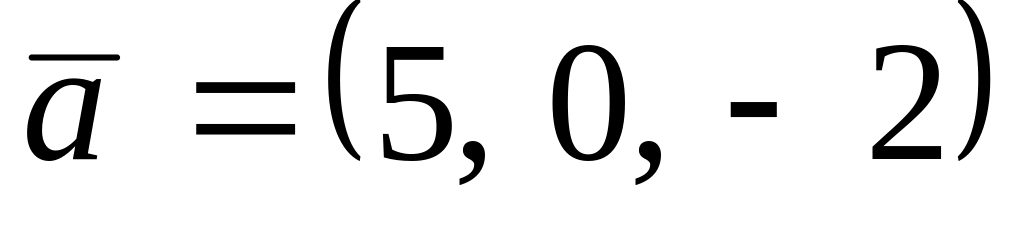 ,
,
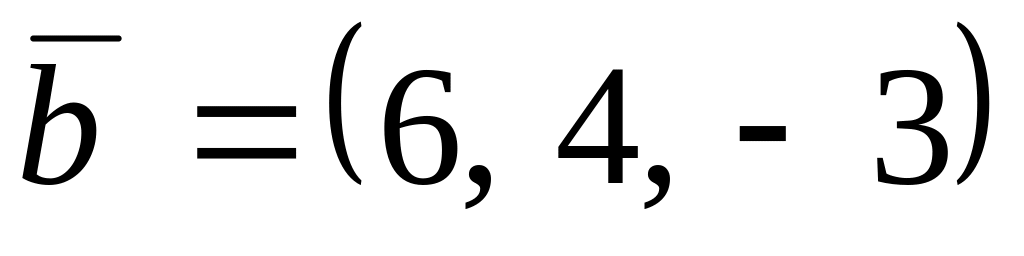 ,
,
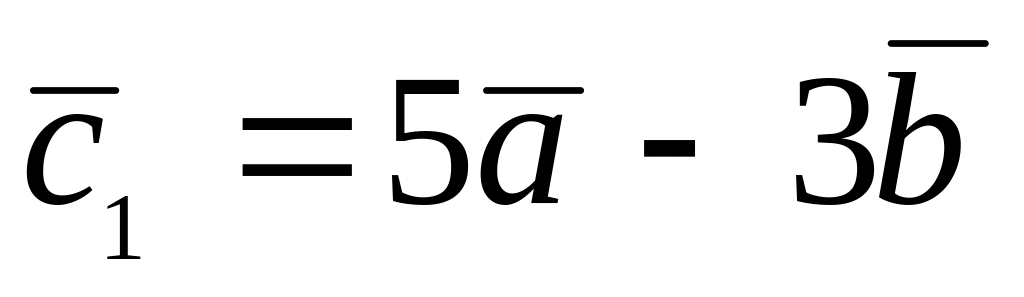 ,
,
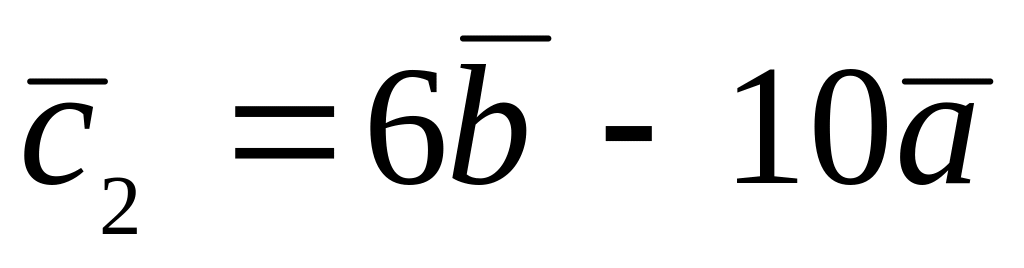 .
.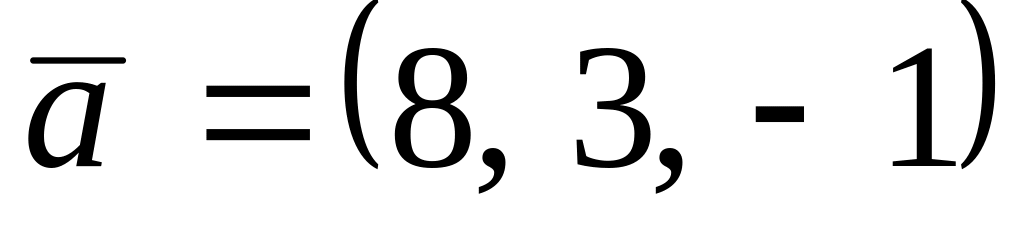 ,
,
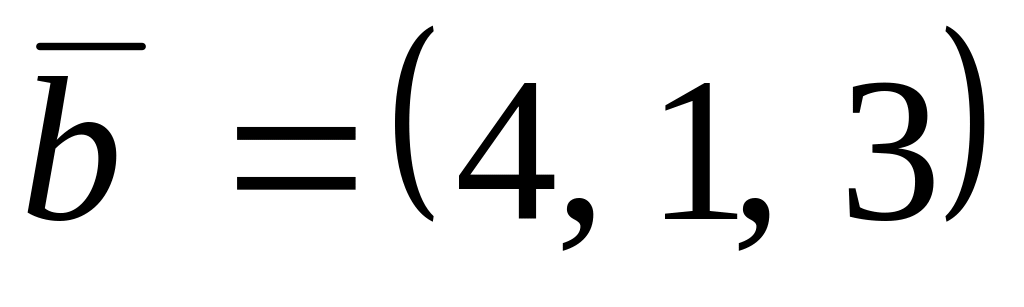 ,
,
,
,
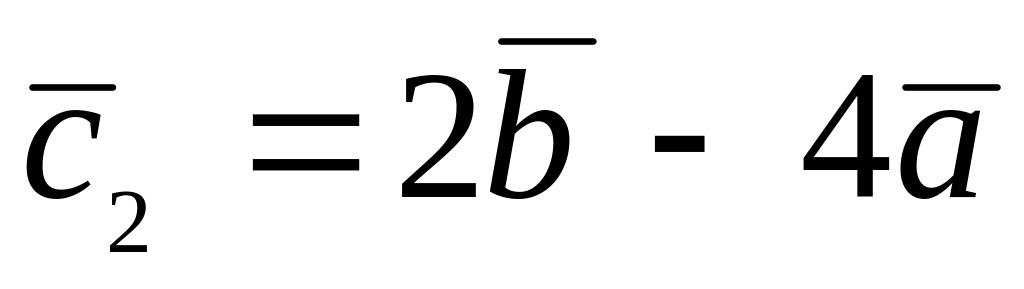 .
.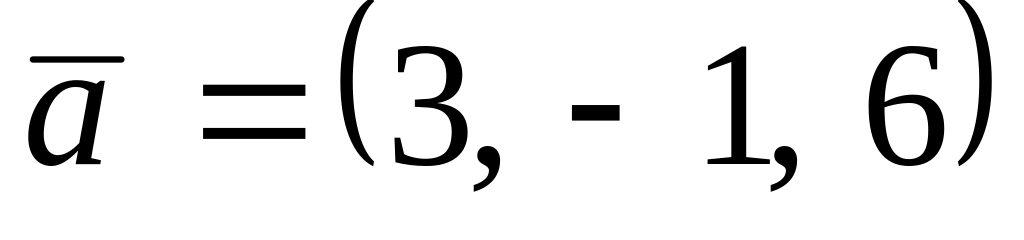 ,
,
 ,
,
.
,
,
.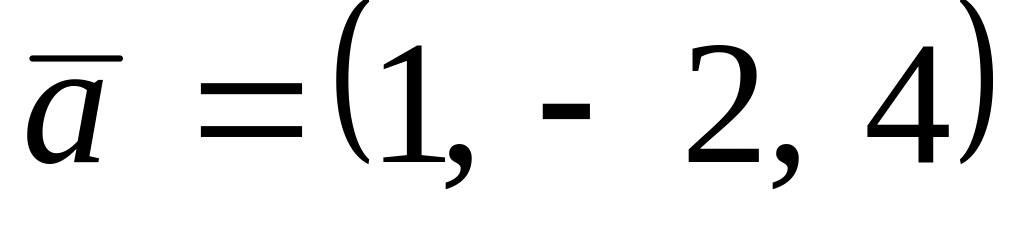 ,
,
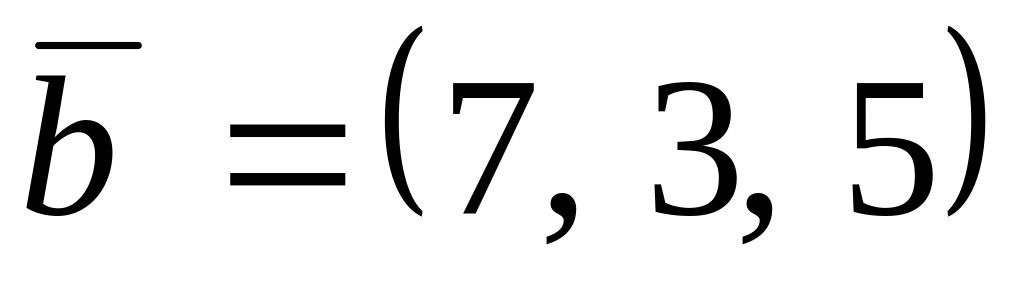 ,
,
.
,
,
. ,
,
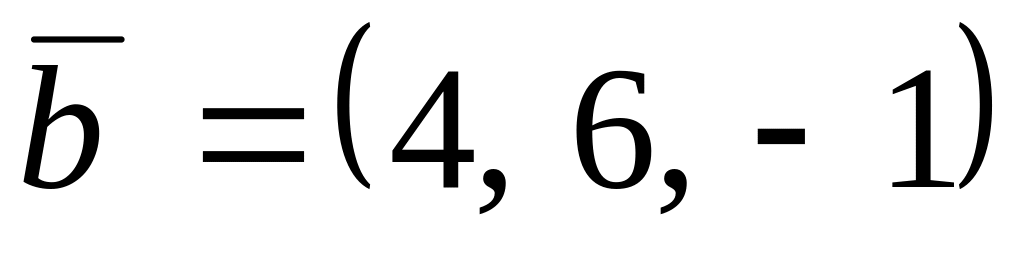 ,
,
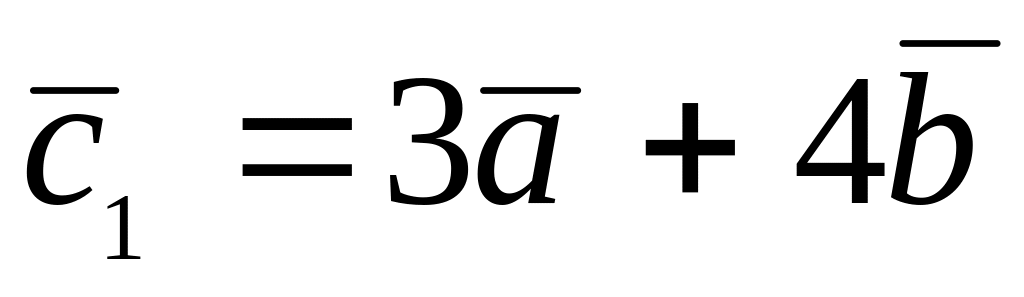 ,
,
 .
. ,
,
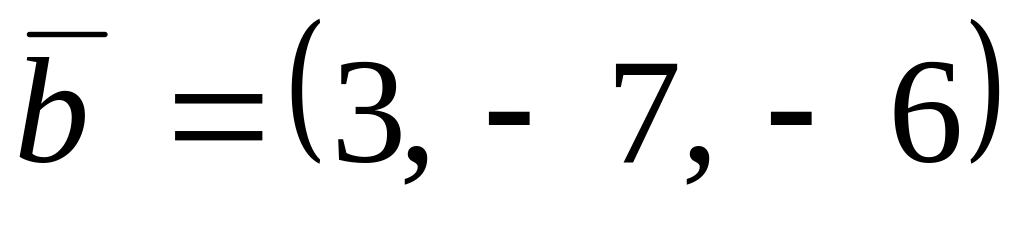 ,
,
 ,
.
,
. ,
,
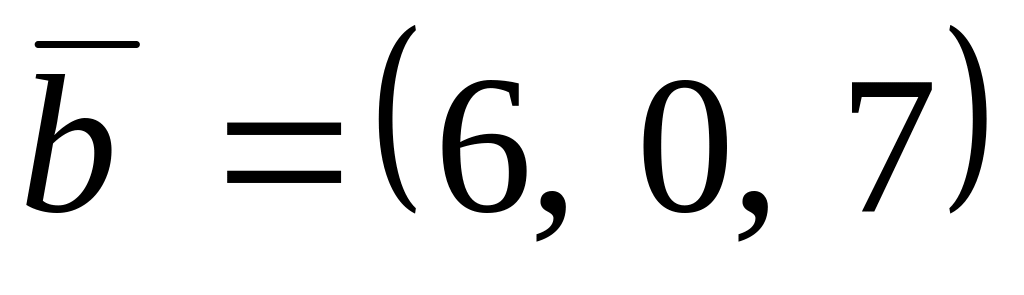 ,
,
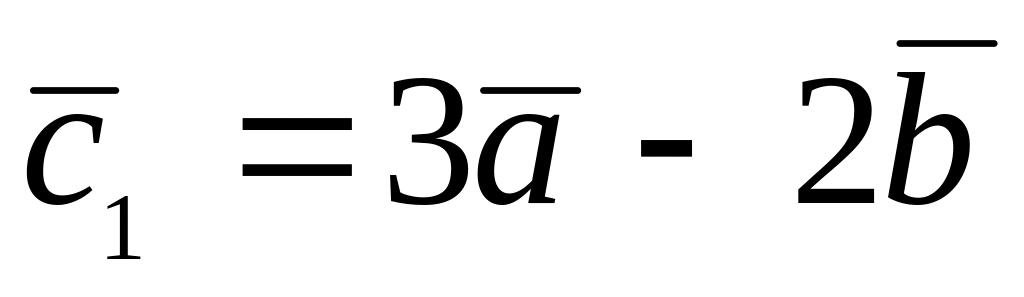 ,
,
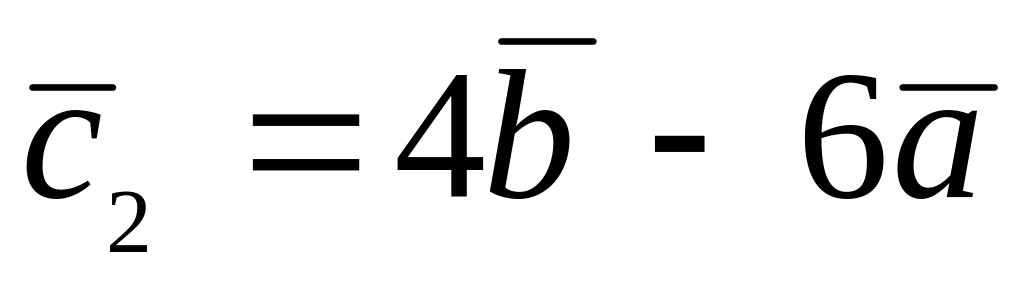 .
.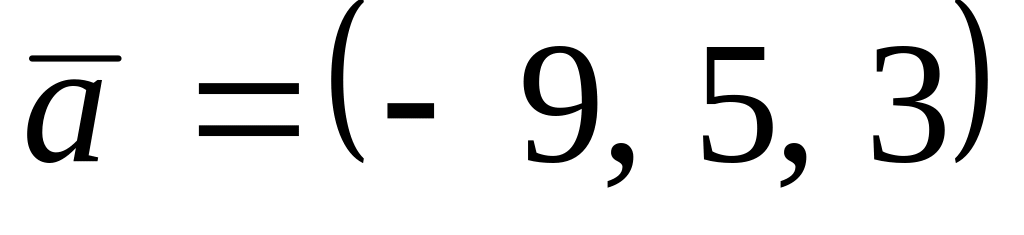 ,
,
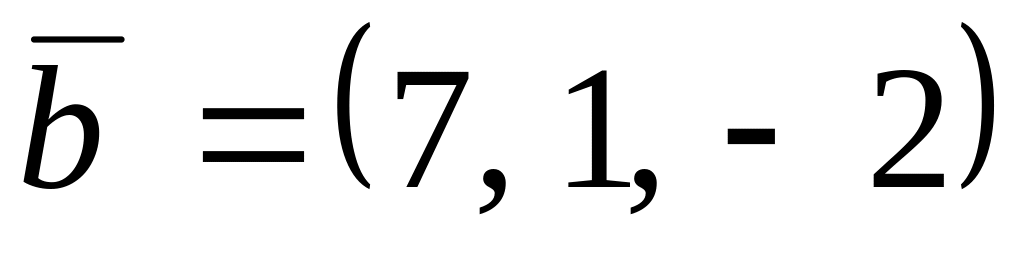 ,
,
,
,
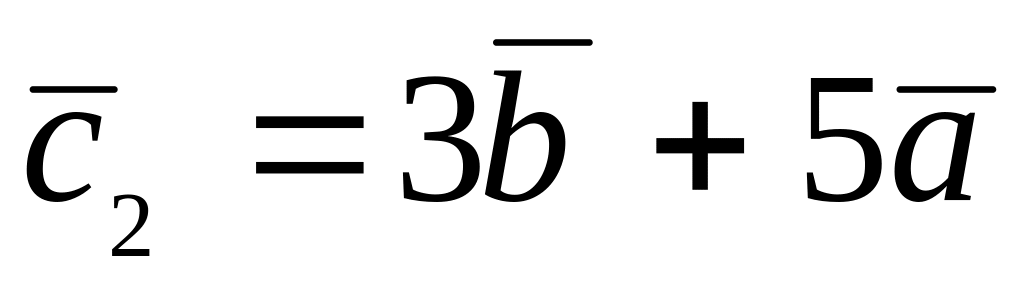 .
.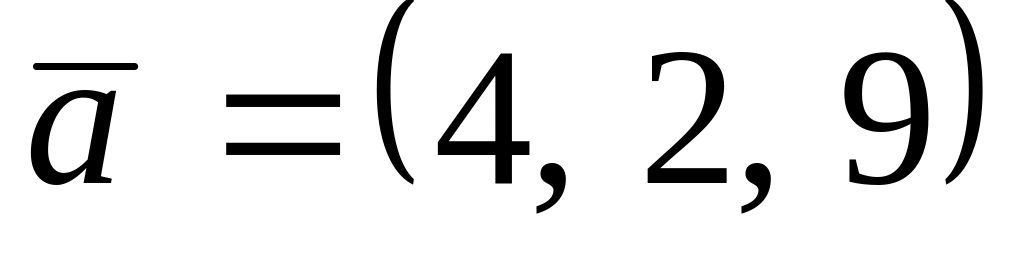 ,
,
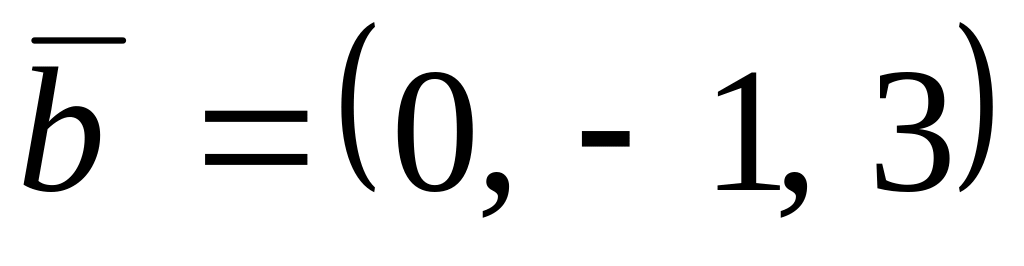 ,
,
 ,
,
 .
. ,
,
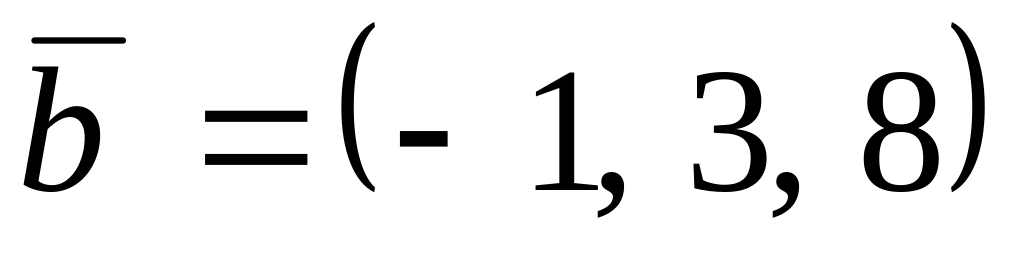 ,
,
,
,
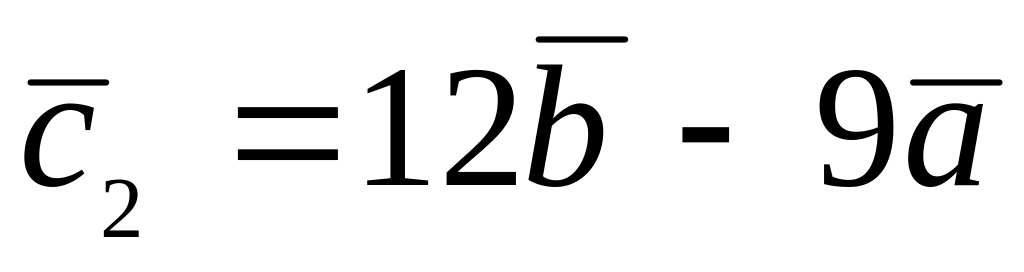 .
.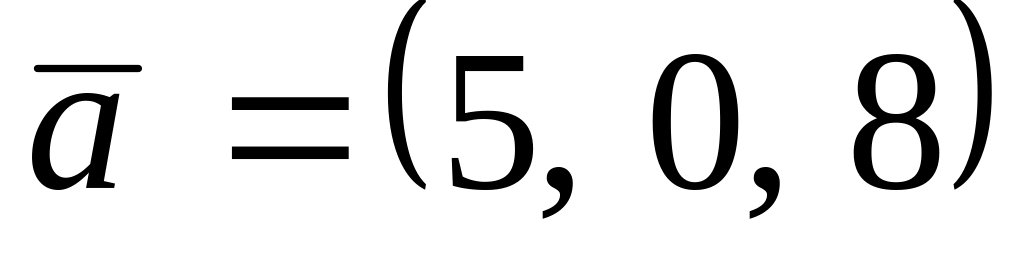 ,
,
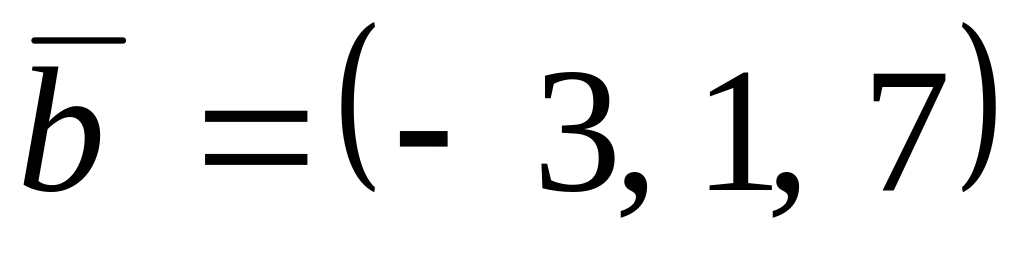 ,
,
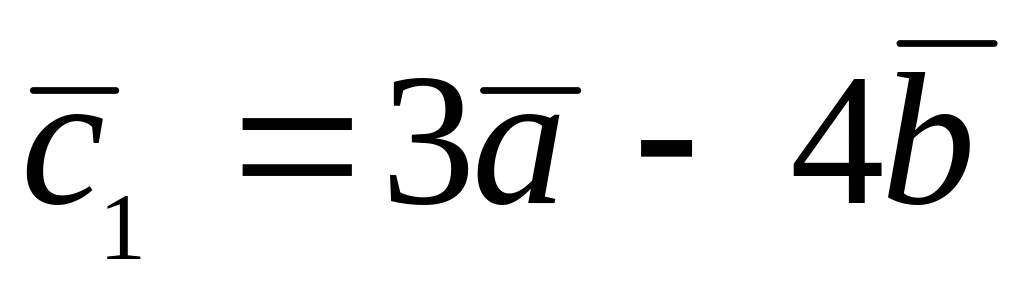 ,
.
,
. ,
,
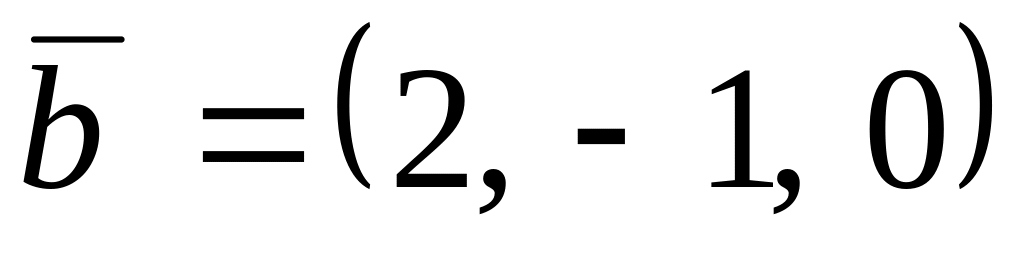 ,
,
.
,
,
.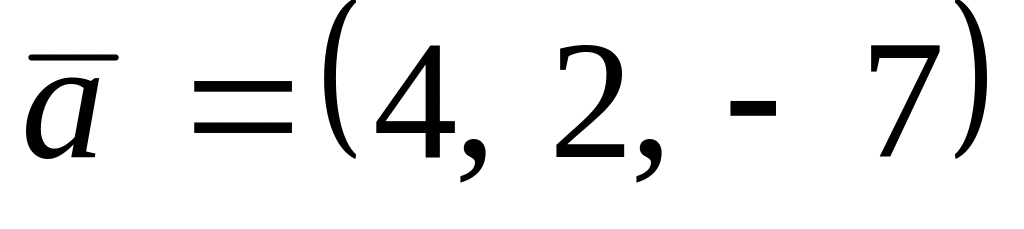 ,
,
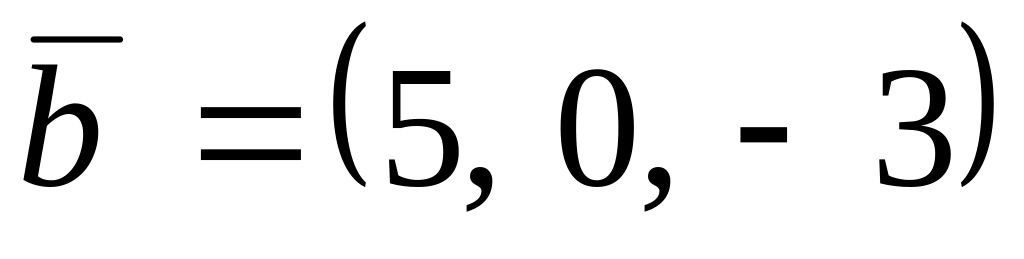 ,
,
 ,
,
 .
.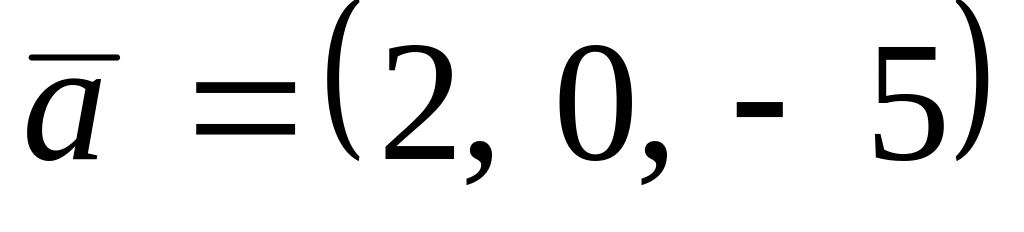 ,
,
,
,
 ,
,
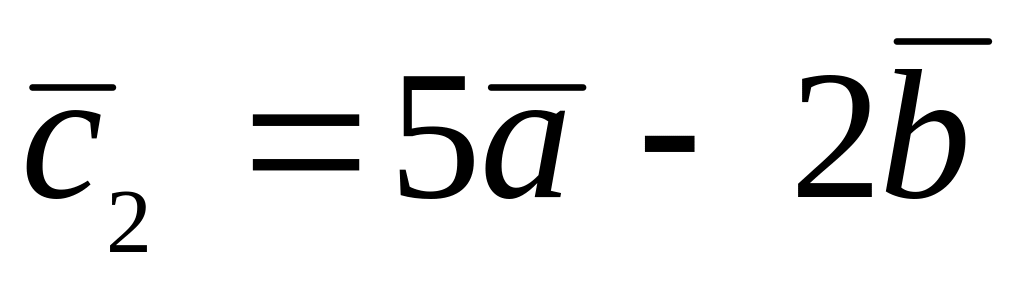 .
.
Задача 4
Компланарны ли векторы
![]() ?
?
![]() ,
,
![]() ,
,
![]()
Решение. По свойствам смешанного
произведения векторов: векторы
![]() ,
,
![]() ,
,
![]() компланарны, если их смешанное произведение
равно нулю, т.е.
компланарны, если их смешанное произведение
равно нулю, т.е.
![]() .
Смешанное произведение векторов в
координатах можно вычислить по формуле:
.
Смешанное произведение векторов в
координатах можно вычислить по формуле:
![]()
Таким образом указанные вектора не компланарны.
Задания для самостоятельного решения
 ,
,
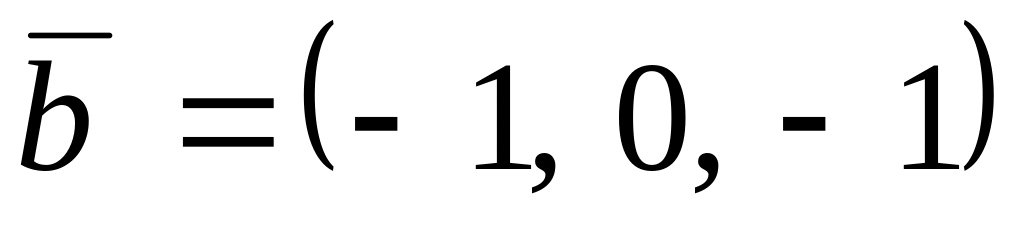 ,
,
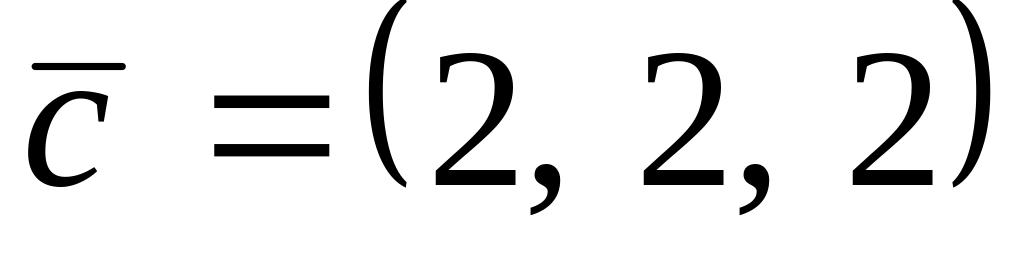 .
.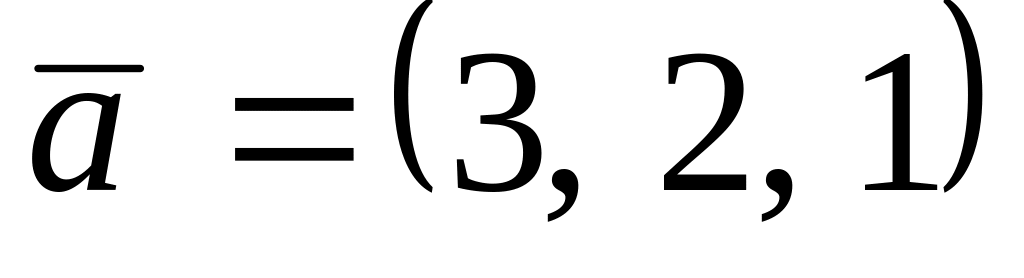 ,
,
 ,
,
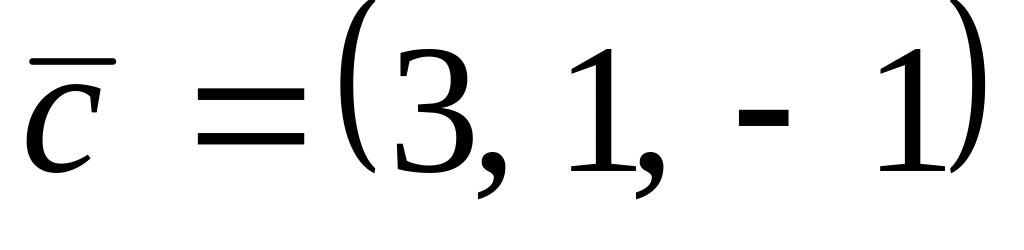 .
. ,
,
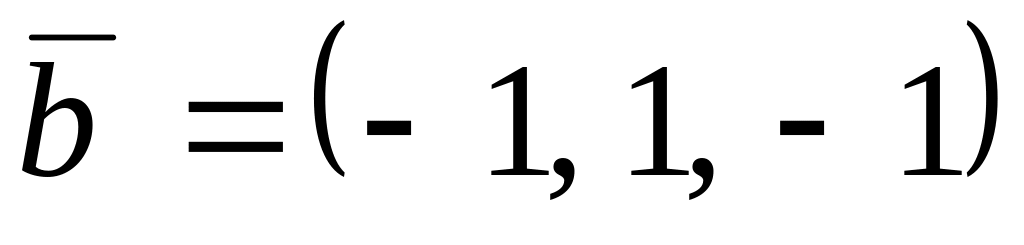 ,
,
 .
. ,
,
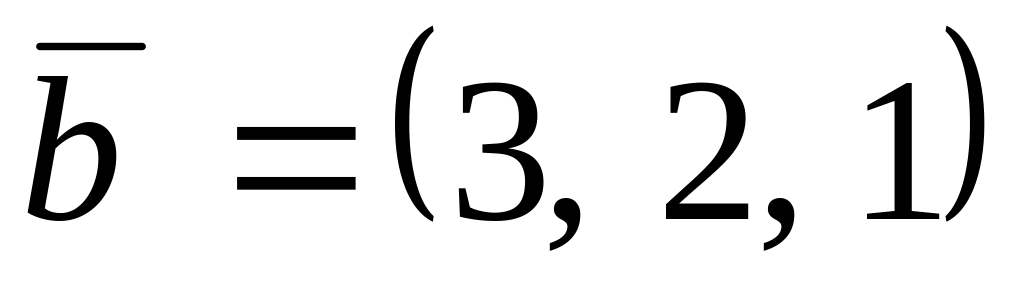 ,
,
 .
.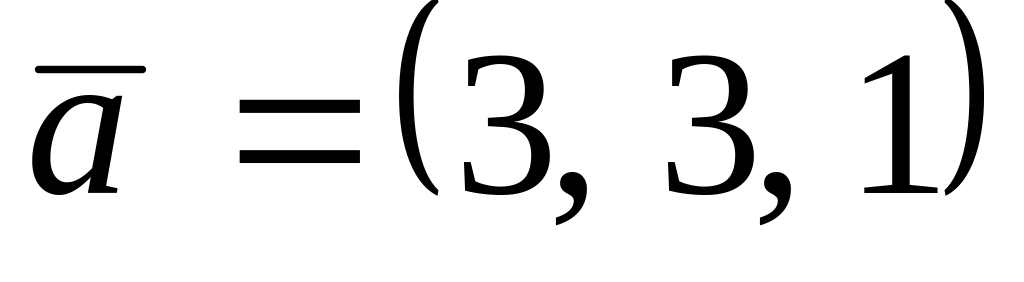 ,
,
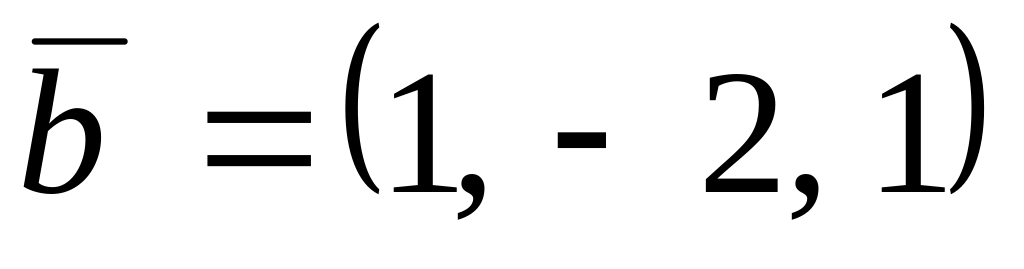 ,
.
,
. ,
,
 ,
,
 .
. ,
,
.
,
,
.,
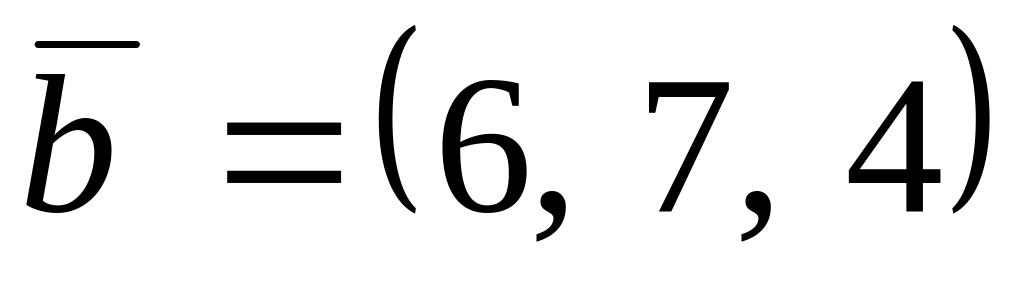 ,
,
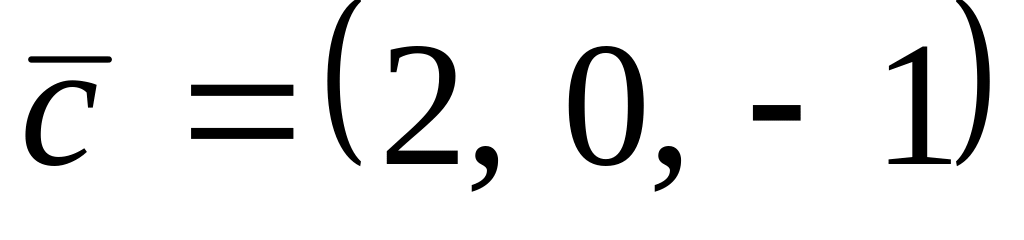 .
.,
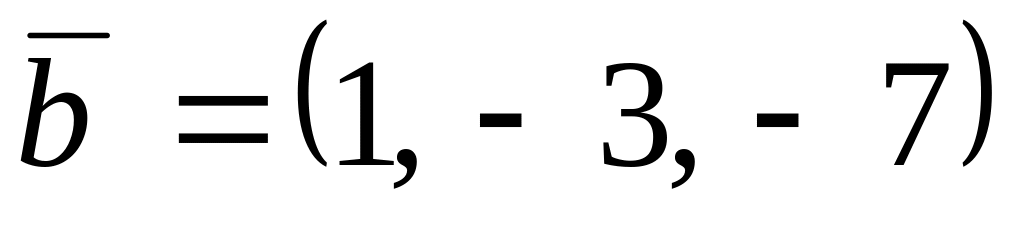 ,
,
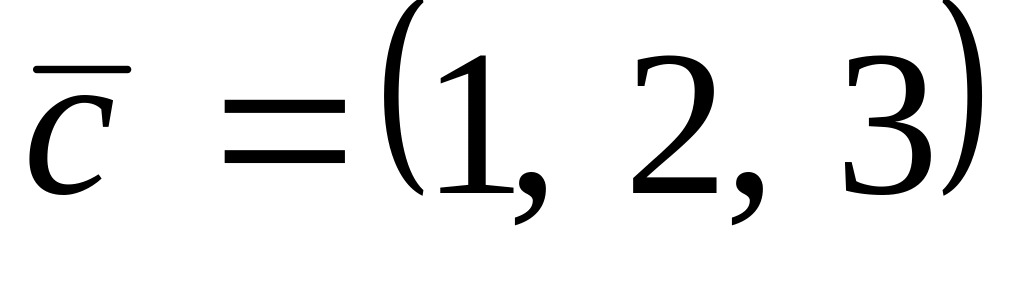 .
.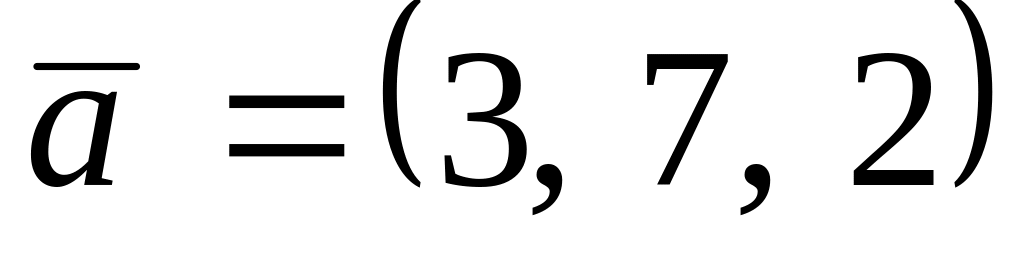 ,
,
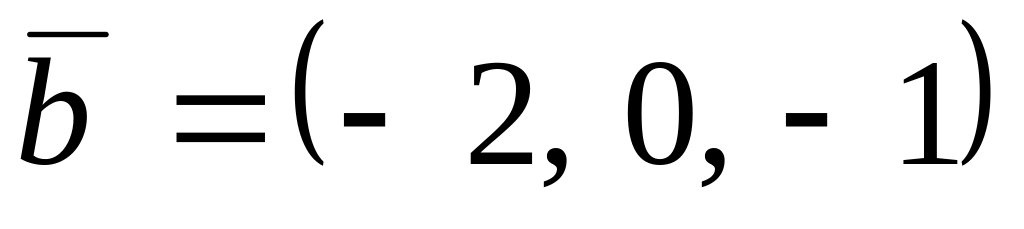 ,
,
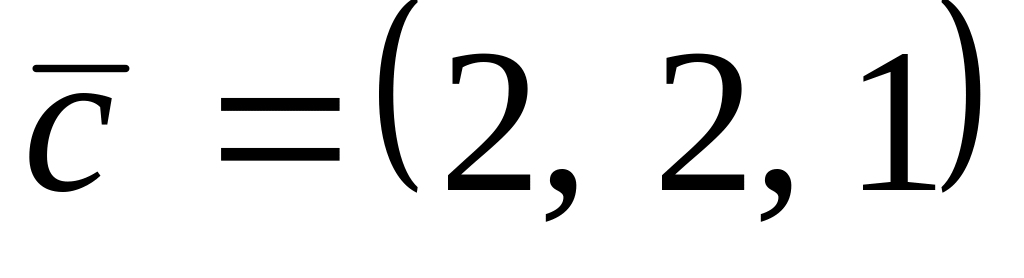 .
.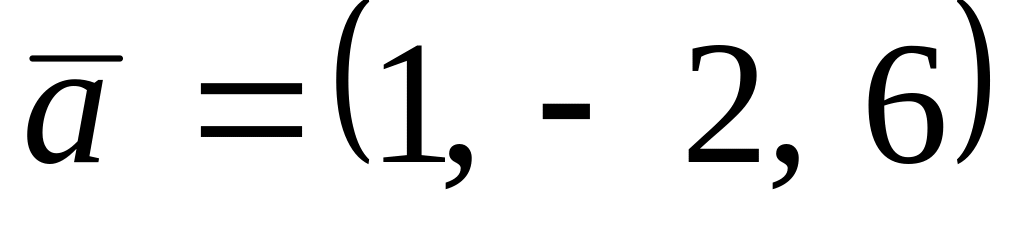 ,
,
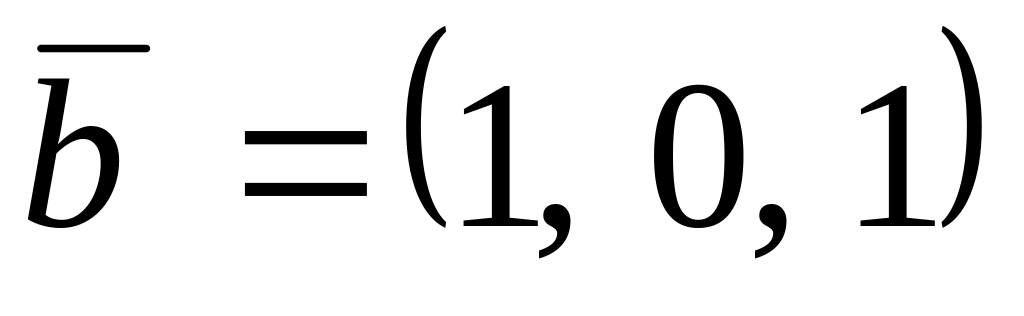 ,
,
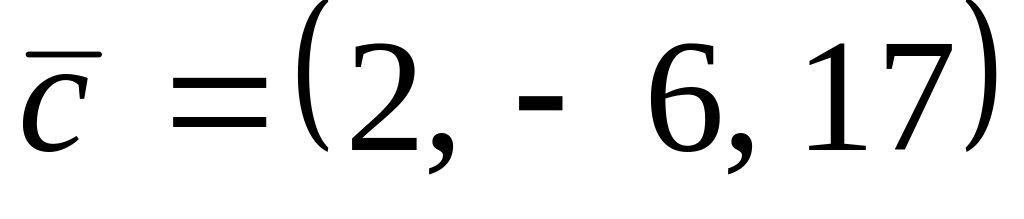 .
.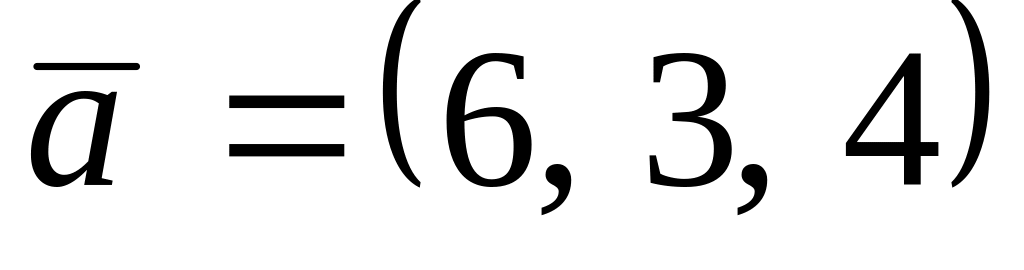 ,
,
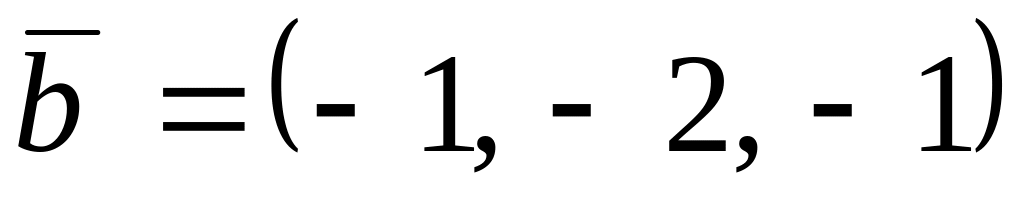 ,
,
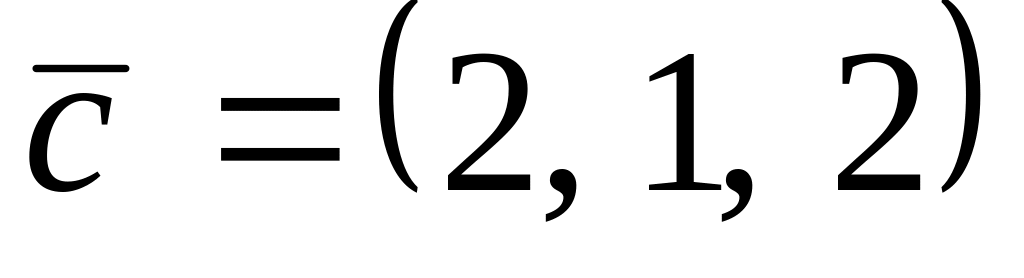 .
. ,
,
,
,
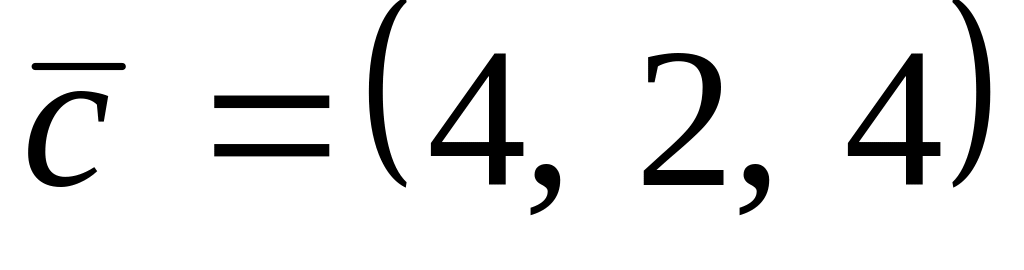 .
.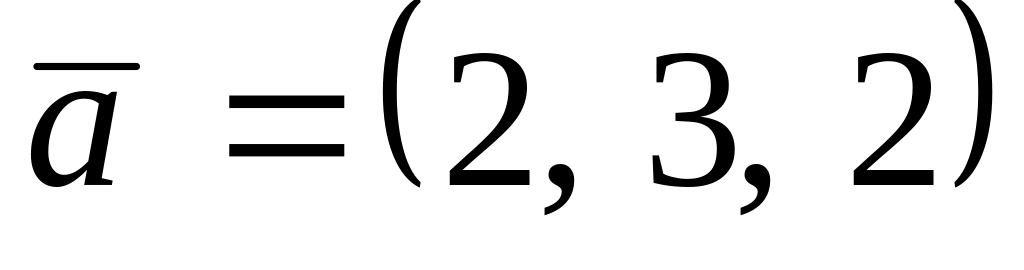 ,
,
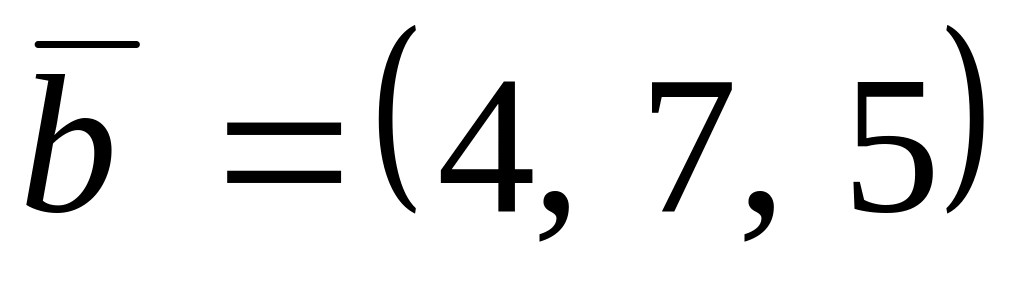 ,
.
,
.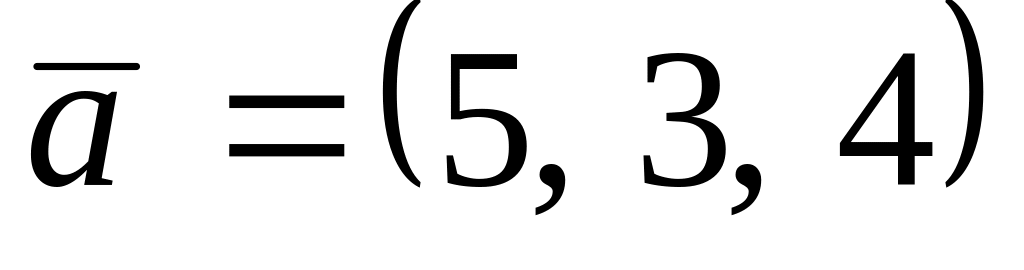 ,
,
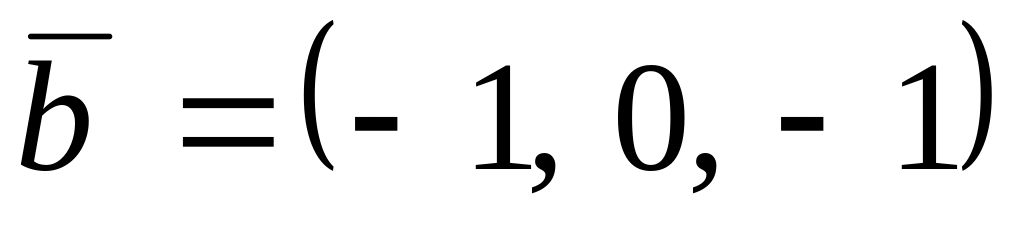 ,
.
,
.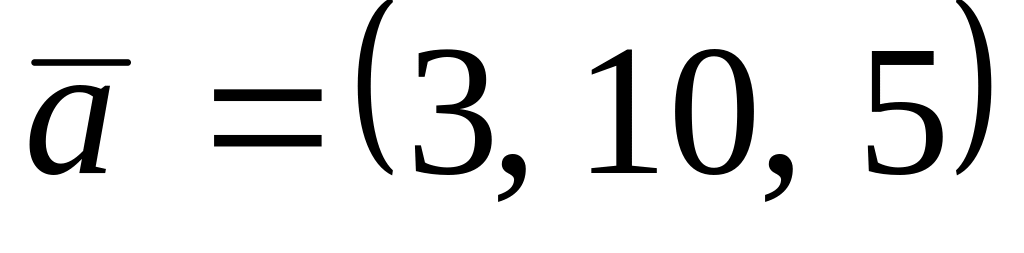 ,
,
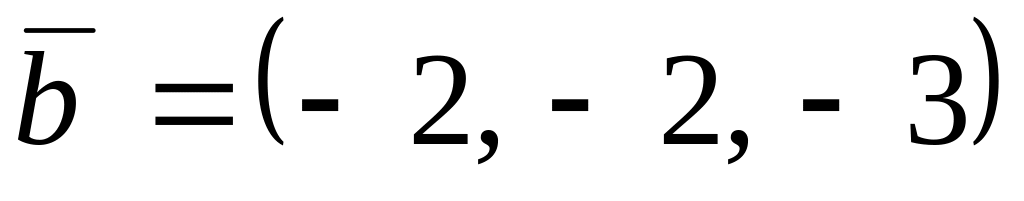 ,
,
 .
.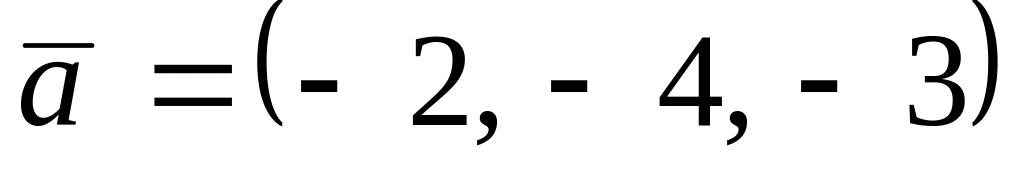 ,
,
 ,
,
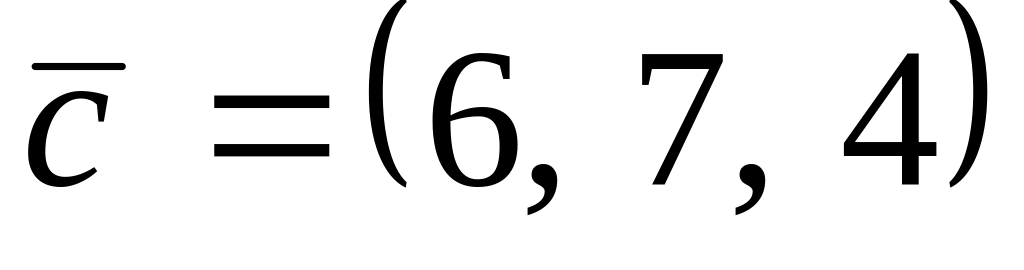 .
.,
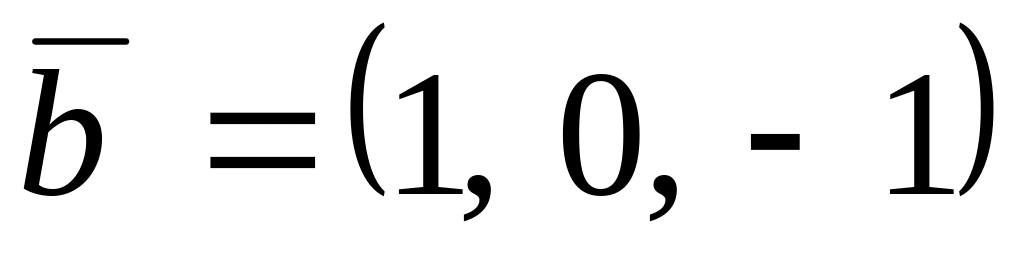 ,
,
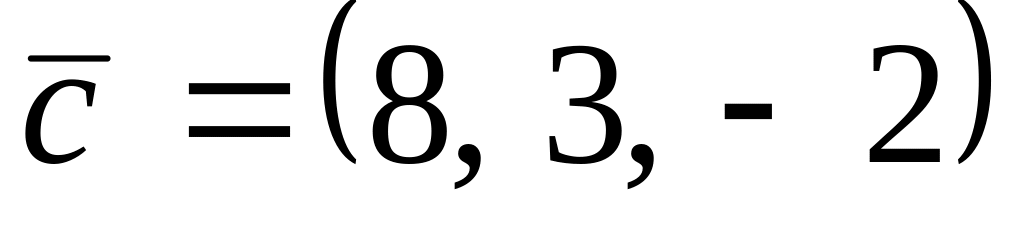 .
. ,
,
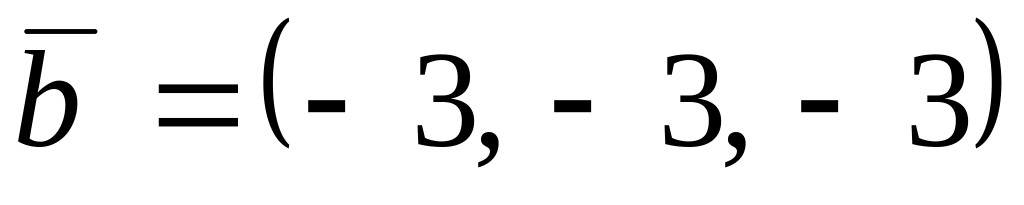 ,
.
,
.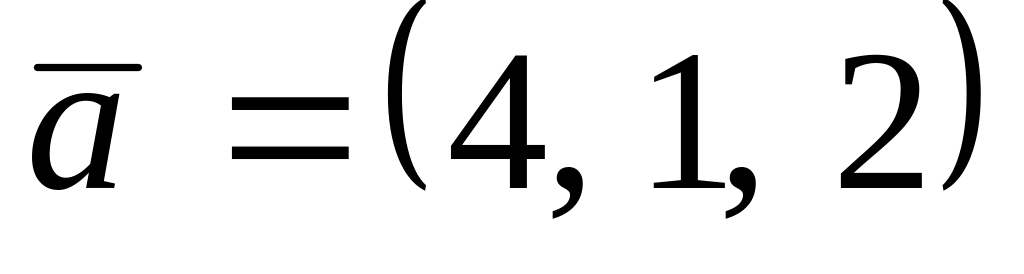 ,
,
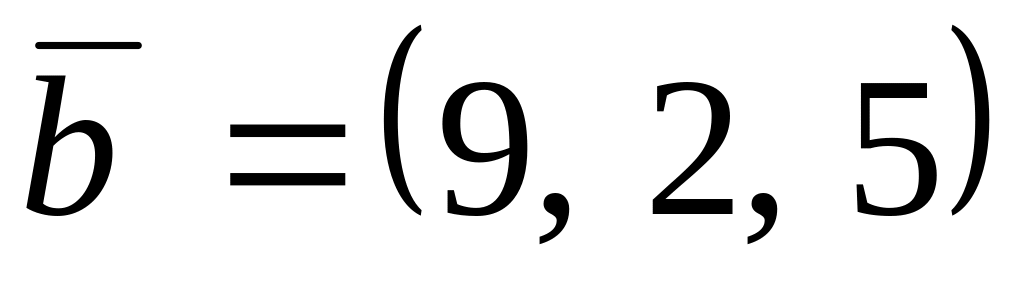 ,
,
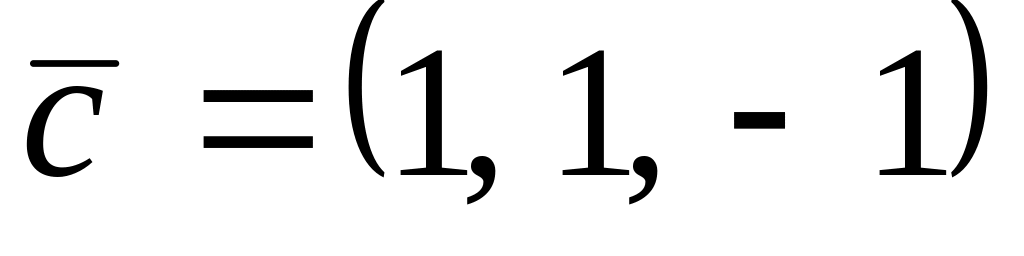 .
.,
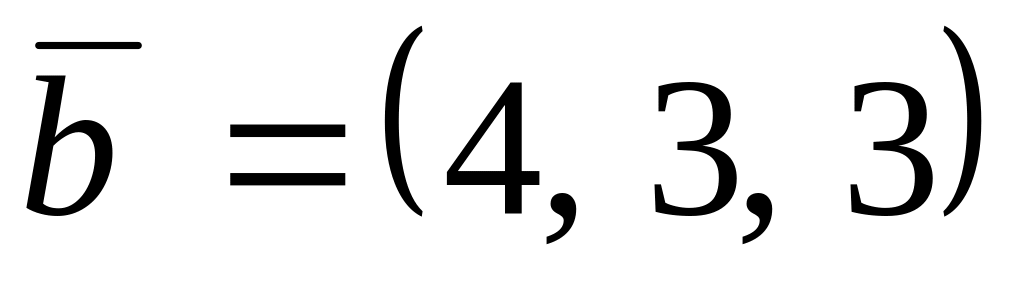 ,
,
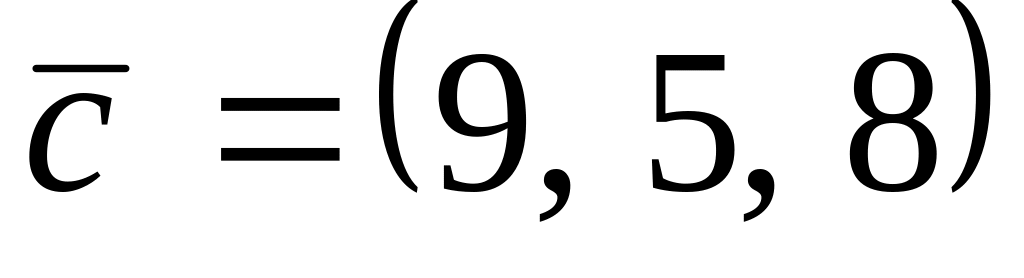 .
.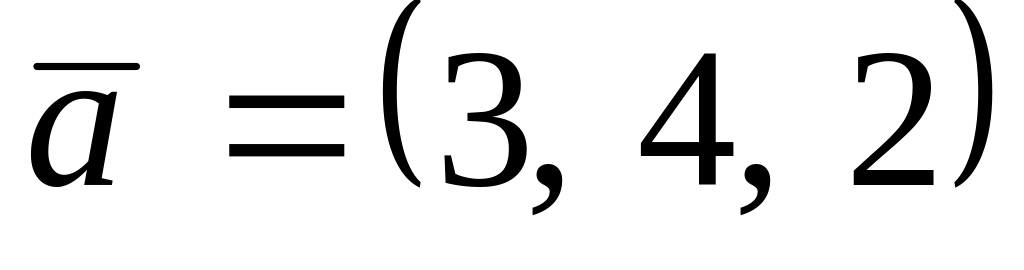 ,
,
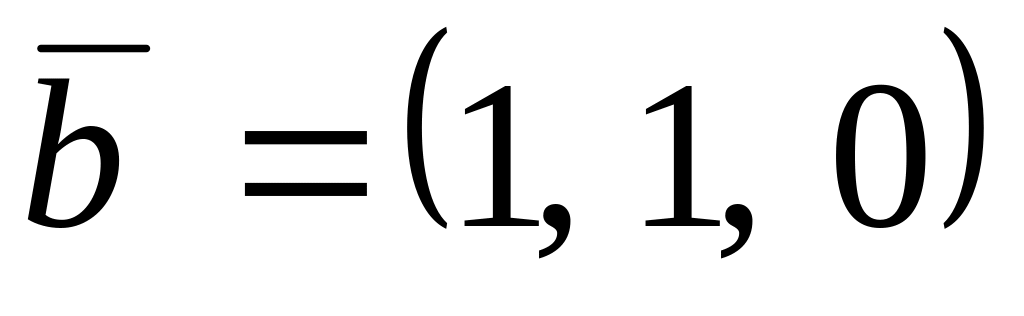 ,
,
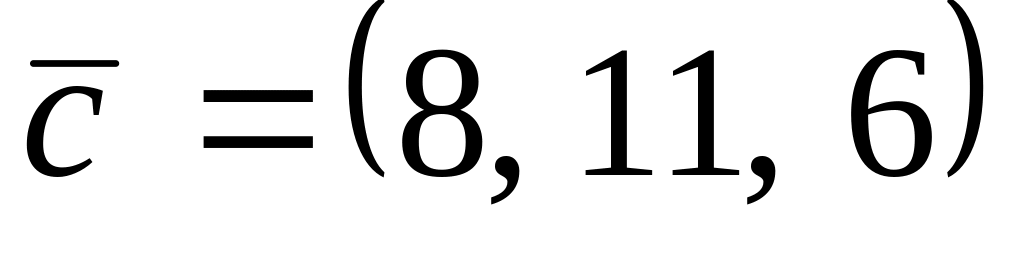 .
.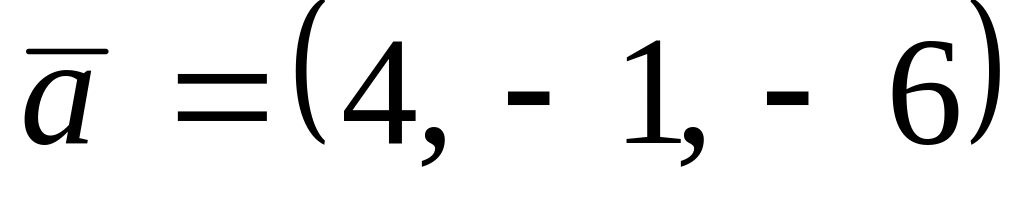 ,
,
,
,
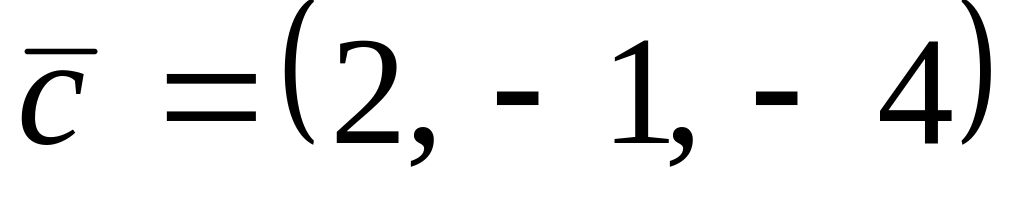 .
. ,
,
 ,
.
,
.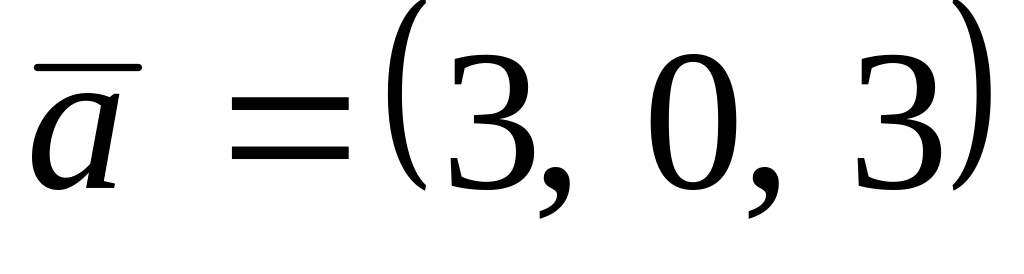 ,
,
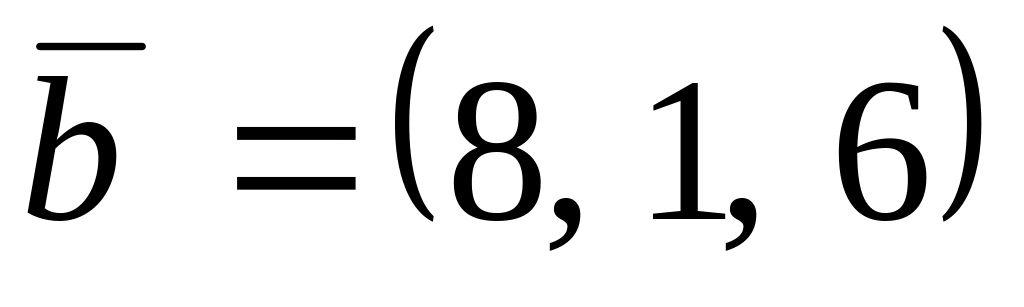 ,
.
,
.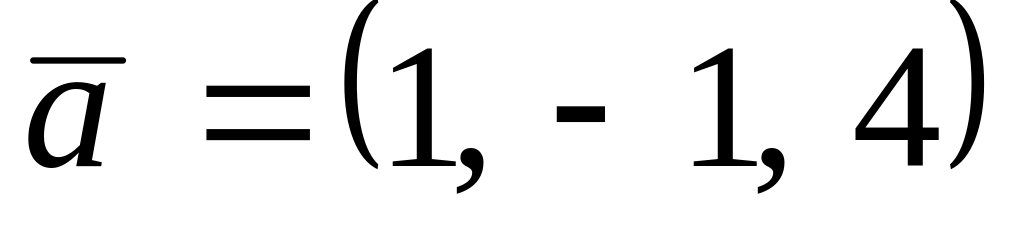 ,
,
 ,
,
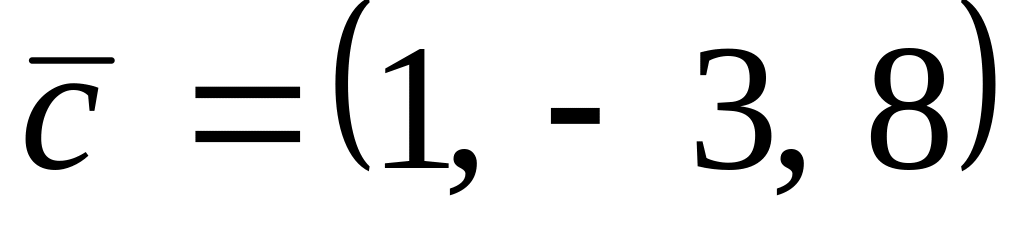 .
., , .
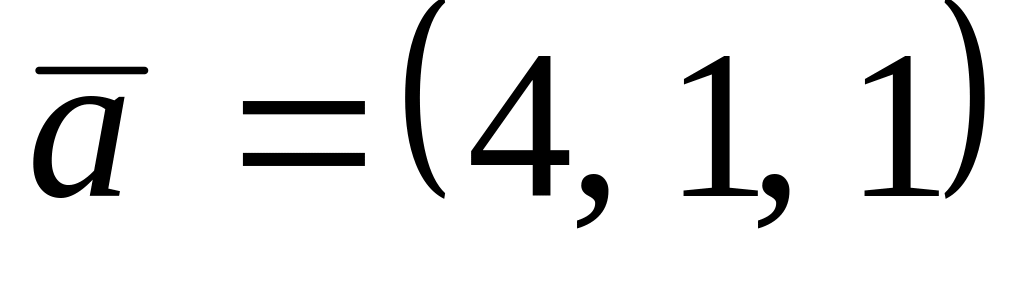 ,
,
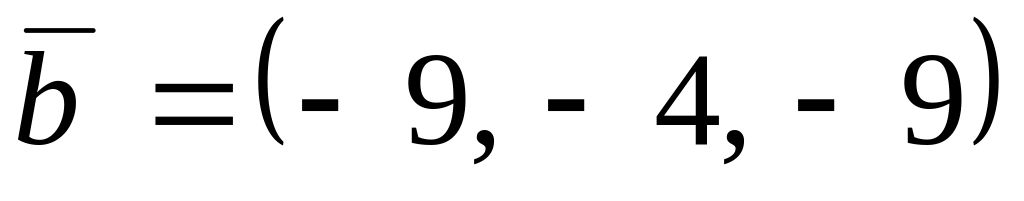 ,
,
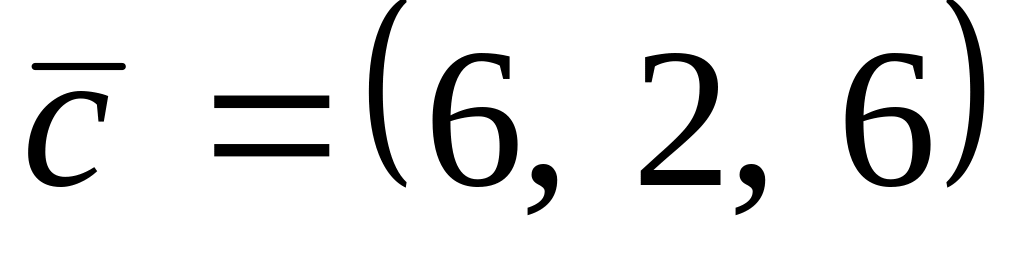 .
. ,
,
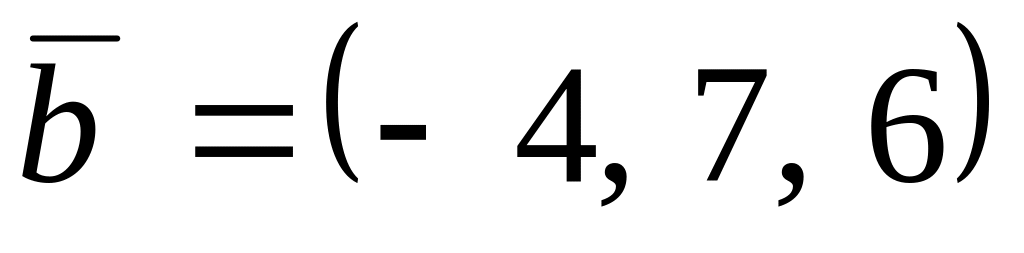 ,
,
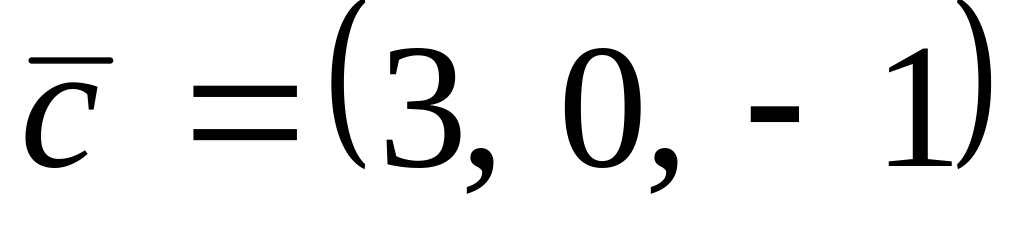 .
. ,
,
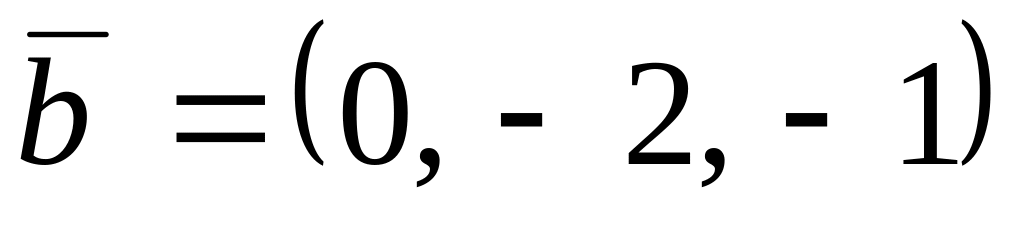 ,
,
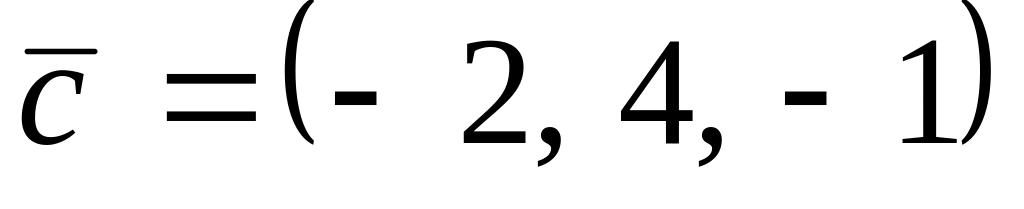 .
.
Группа в Задача 1
Вычислить определители.
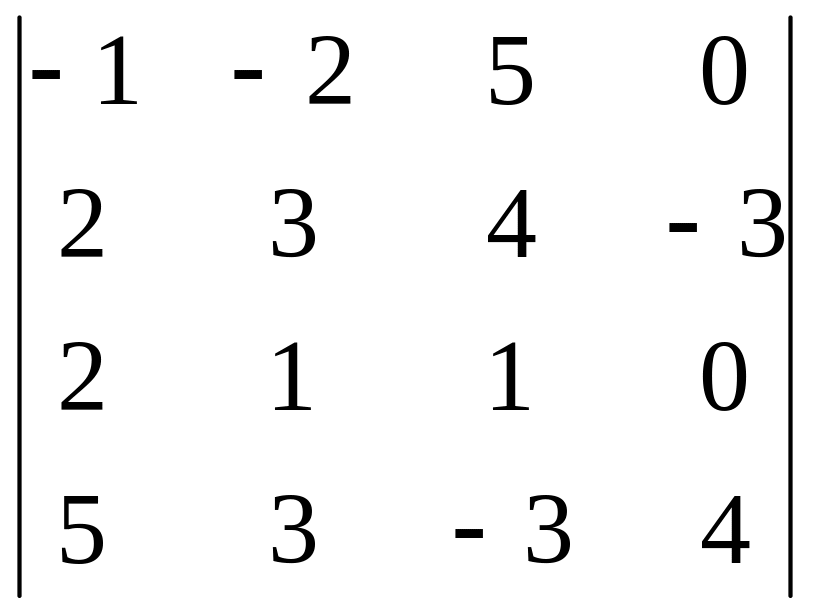 .
.
Решение. разложим определитель по третьему столбцу, т.к. в этом столбце есть два нулевых элемента.
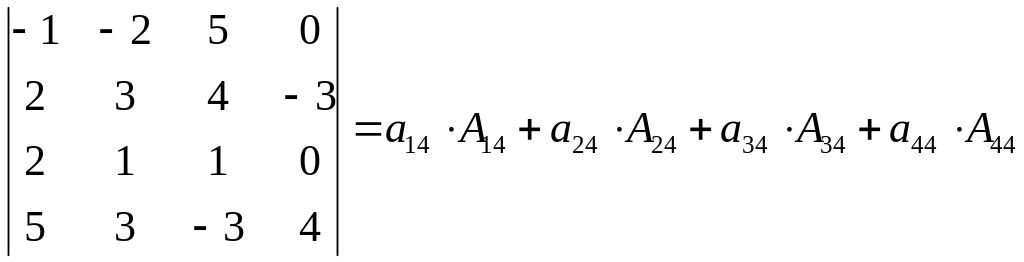 ,
,
где
![]() ,
а
,
а
![]() минор для элемента
минор для элемента
![]() ,
который получается из исходного
определителя путем вычеркивания
,
который получается из исходного
определителя путем вычеркивания
![]() - строки и
- строки и
![]() - столбца.
- столбца.
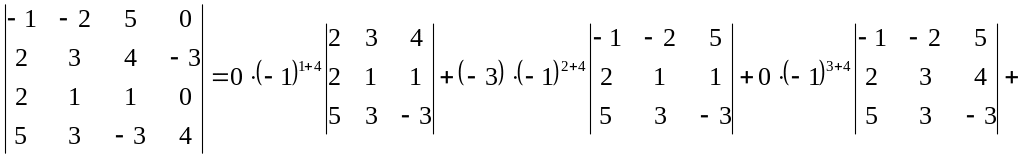
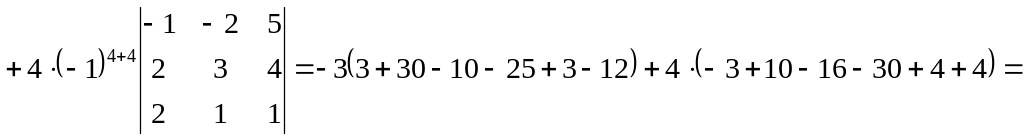
![]() .
.
Определители третьего порядка были вычислены по правилу треугольника.
Задания для самостоятельного решения
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|