Задания для самостоятельного решения

1. , .

2. , .

3. , .

4. , .

5. , .

6. , .

7. , .

8. , .

9. , .

10. , .

11. , .

12. , .

13. , .

14. , .

15. , .

16. , .

17. , .

18. , .

19. , .

20. , .

21. , .

22. , .

23. , .

24. , .

25. , .

26. , .

27. , .

28. , .

29. , .

30. ,

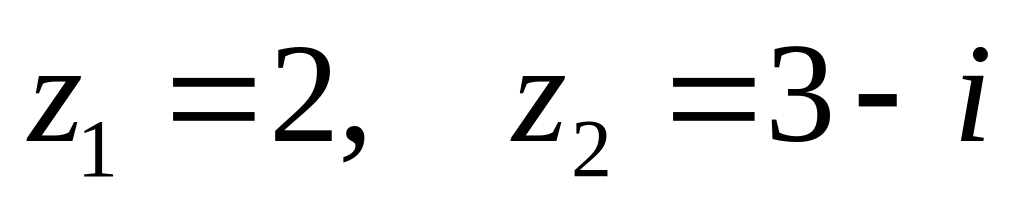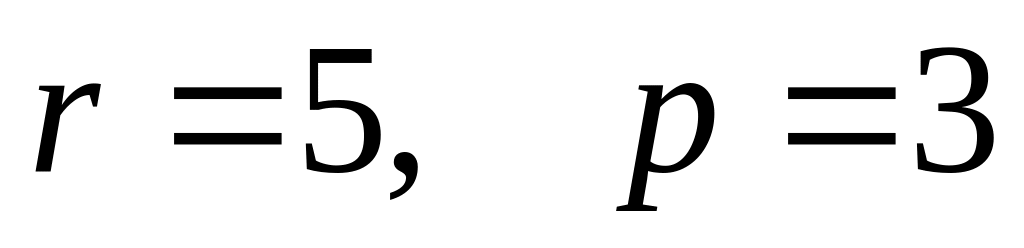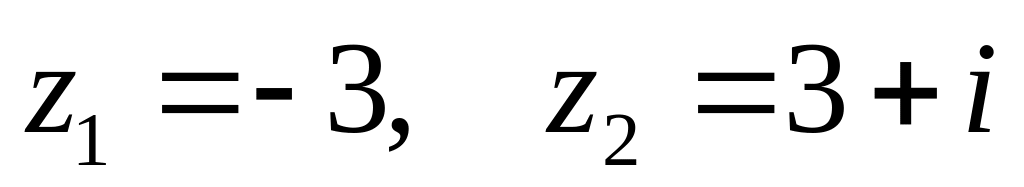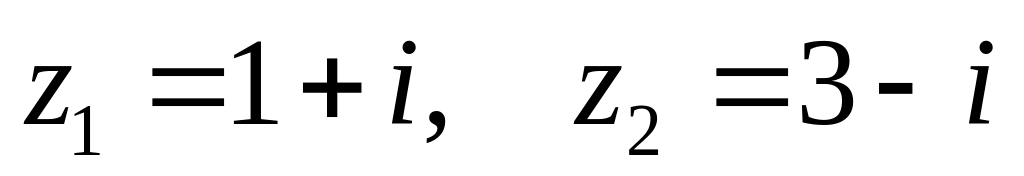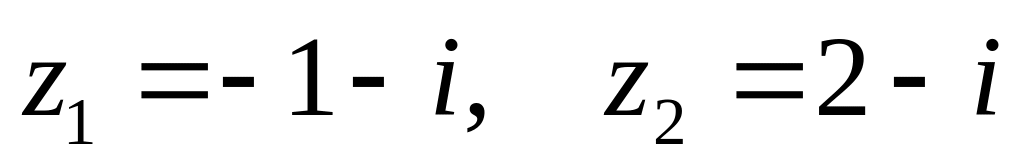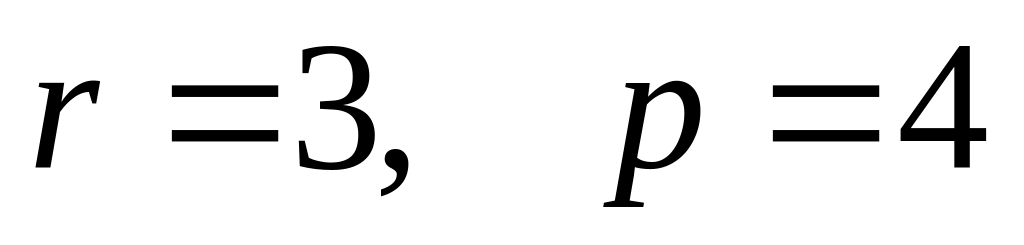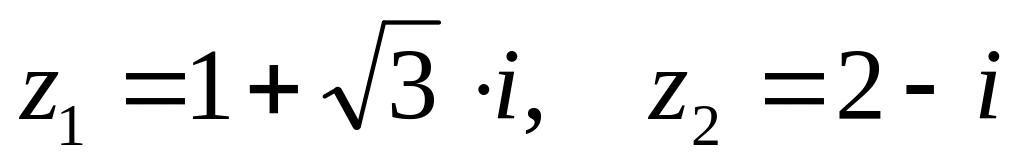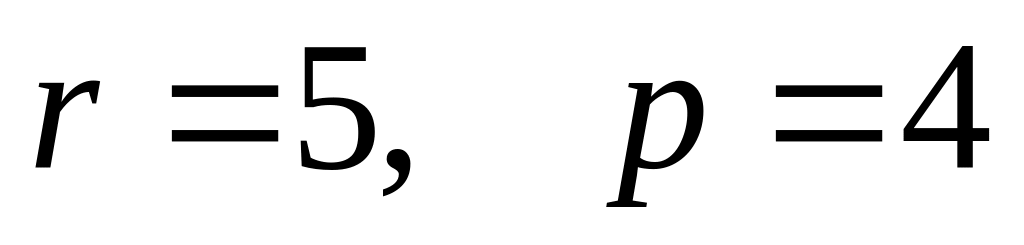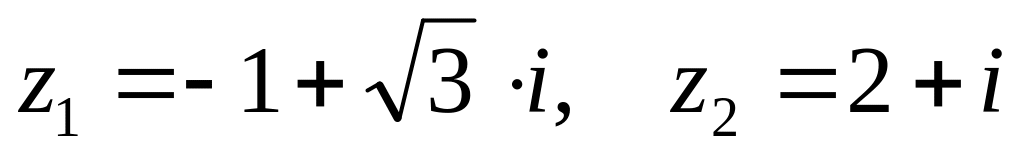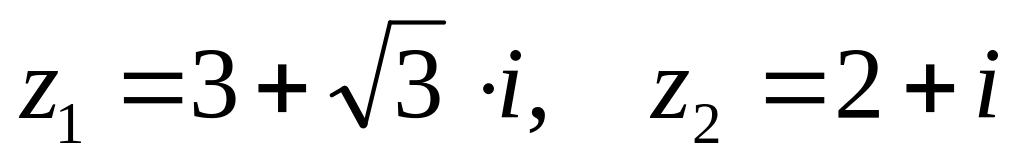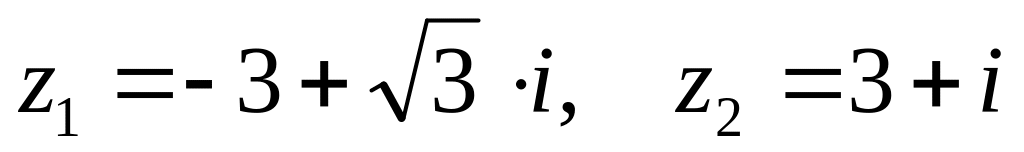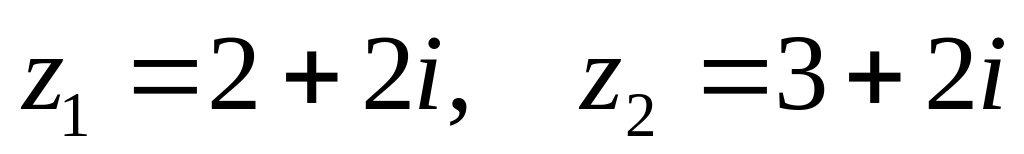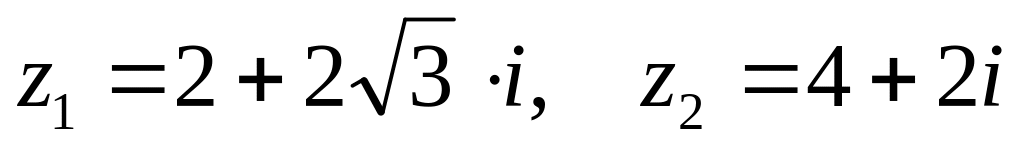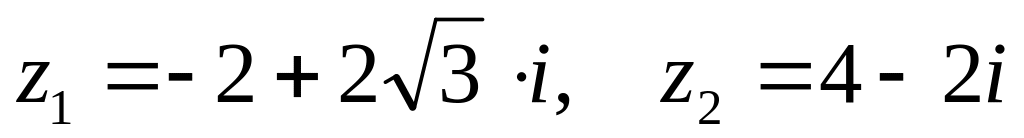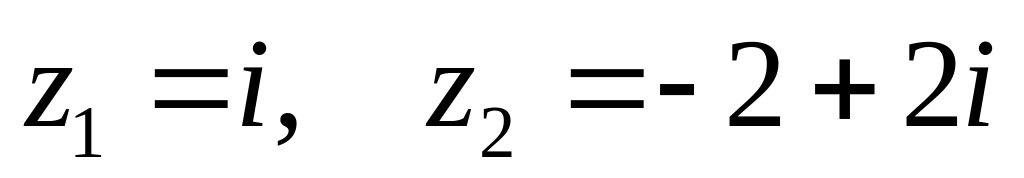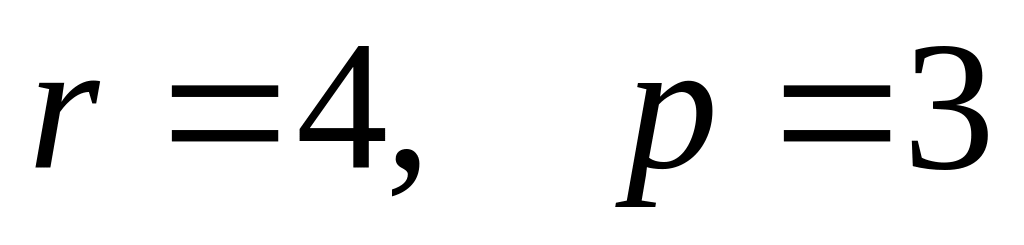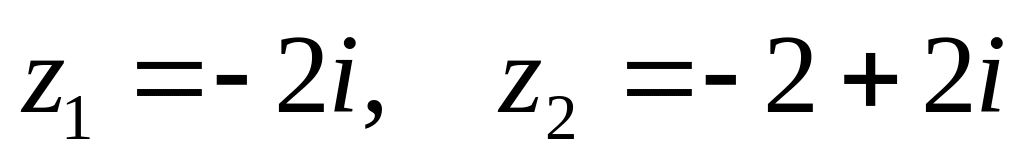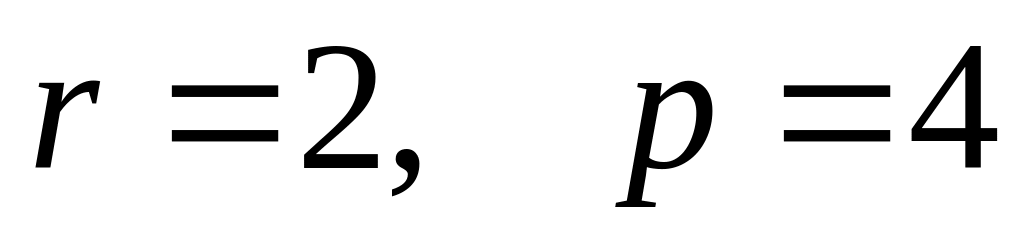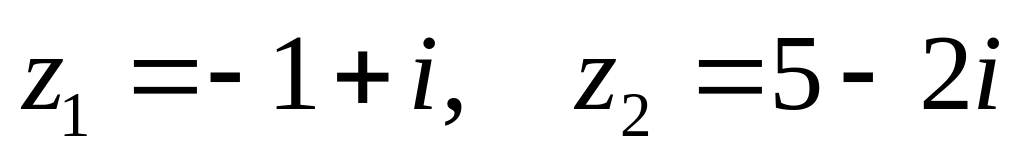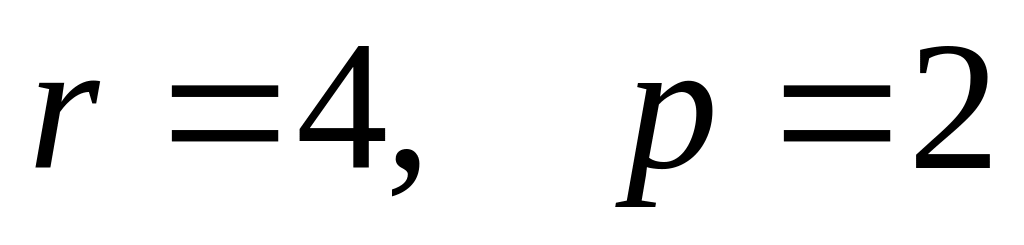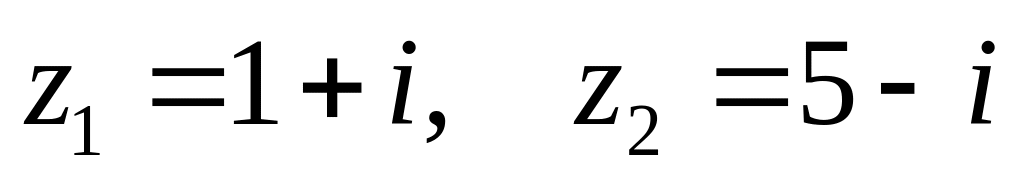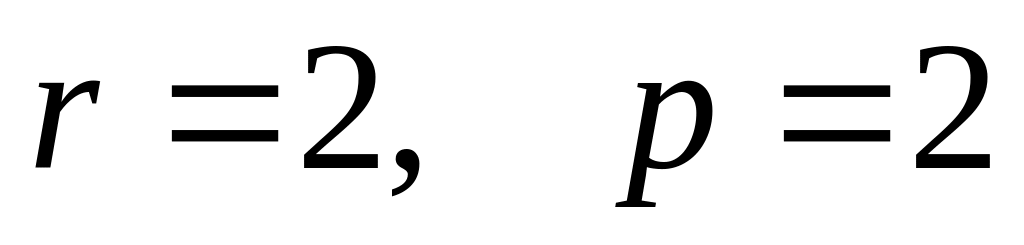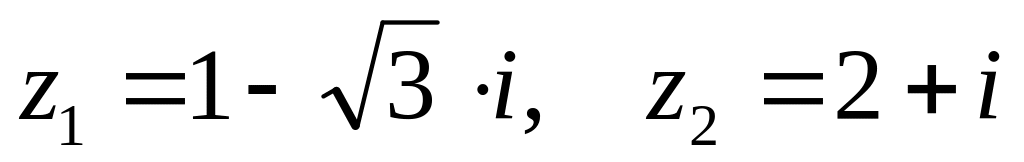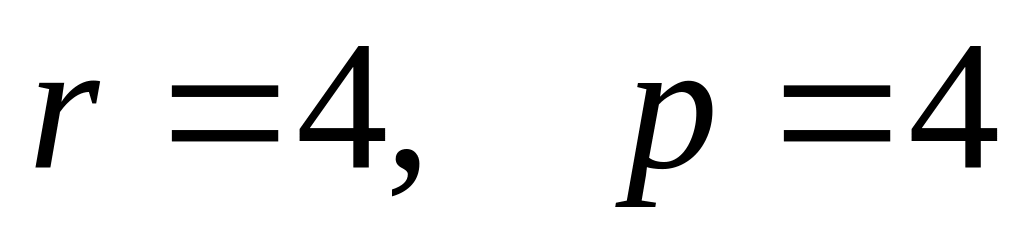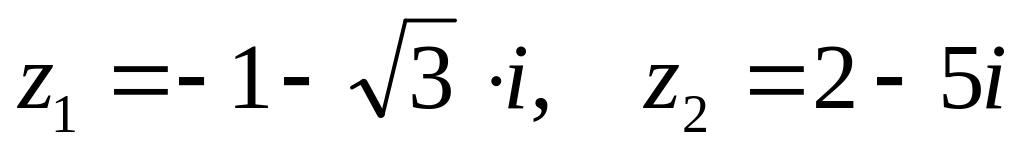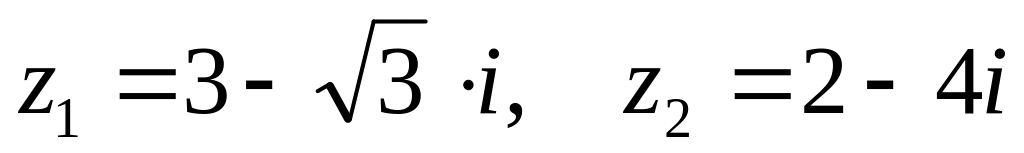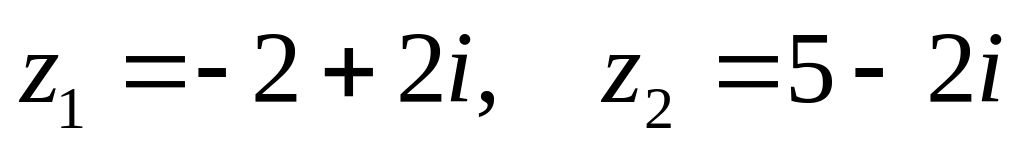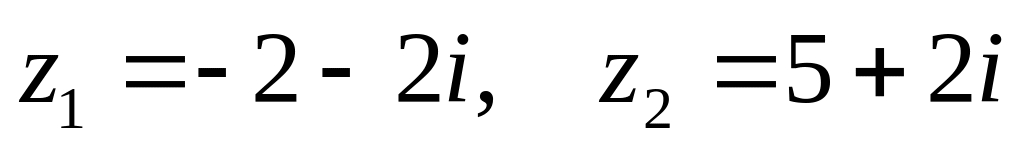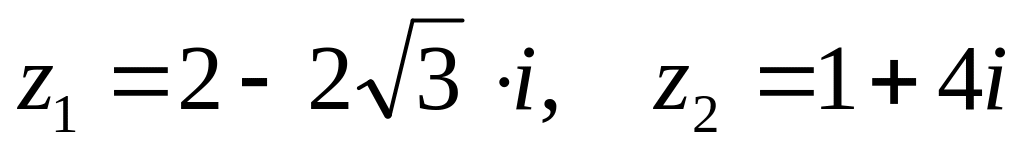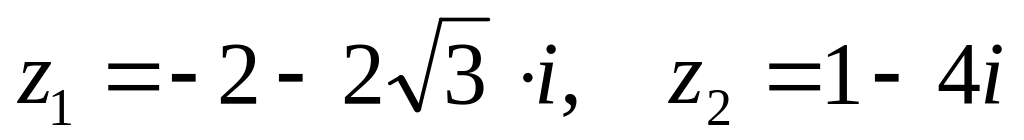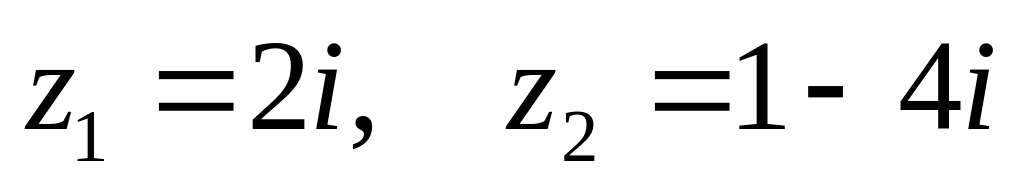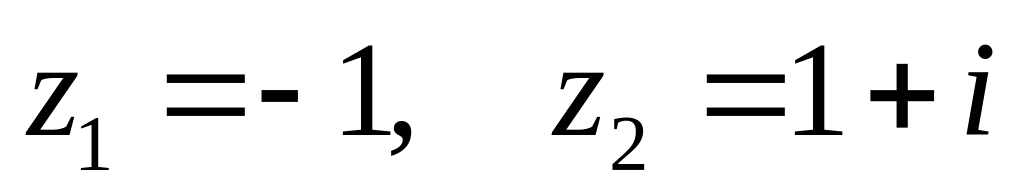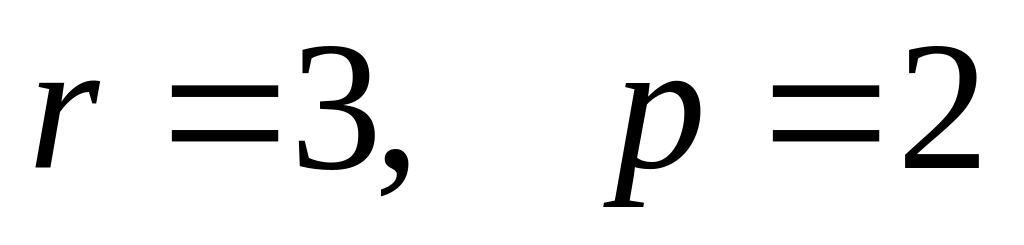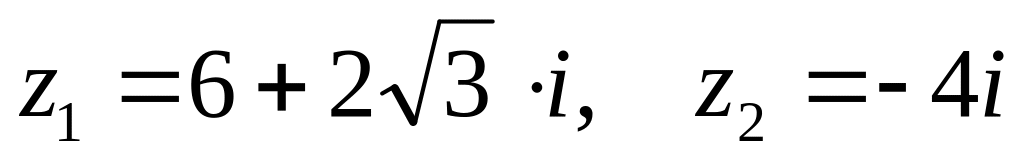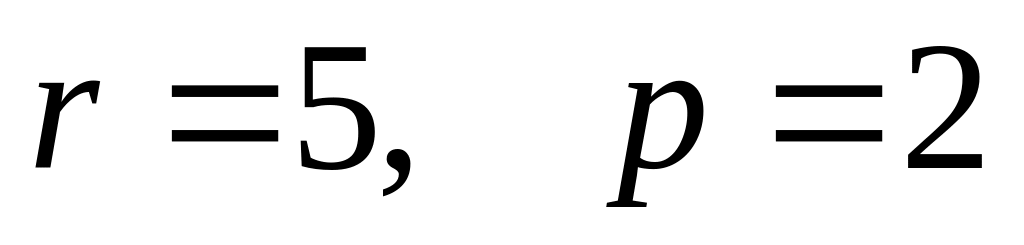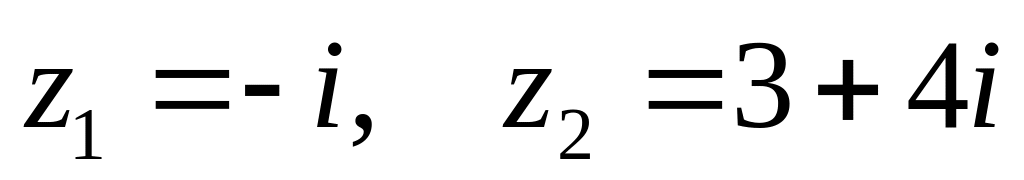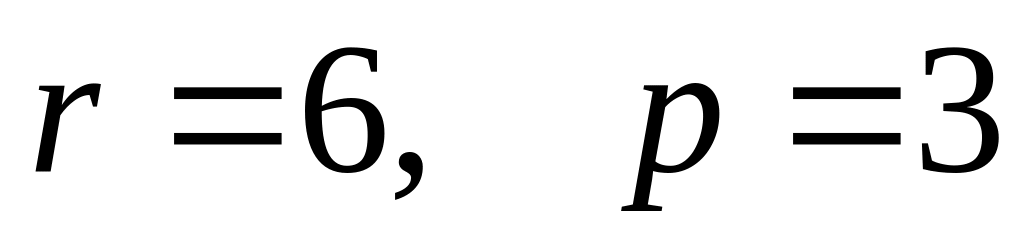
Группа в. Задача1

Исследовать функцию и построить график.

Решение. пусть дана функция

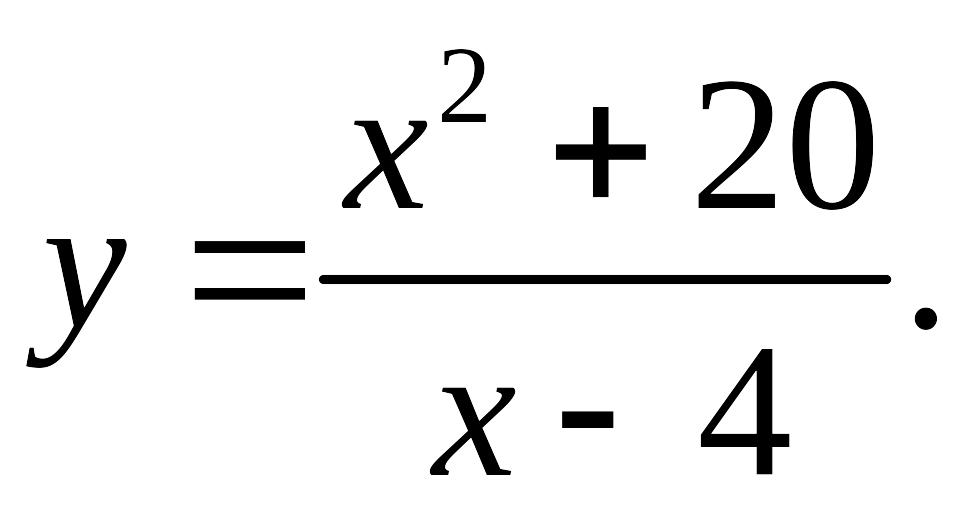
1. Область определения.

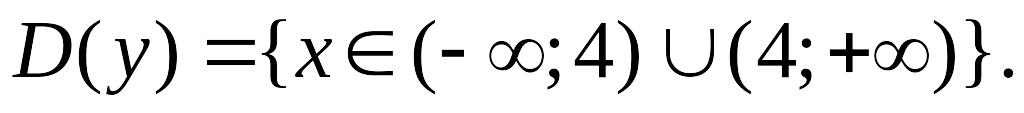
2. Исследование на непрерывность и классификация точек разрыва.

Заданная функция непрерывна всюду, кроме точки х = 4. Вычислим ее односторонние пределы в этой точке:

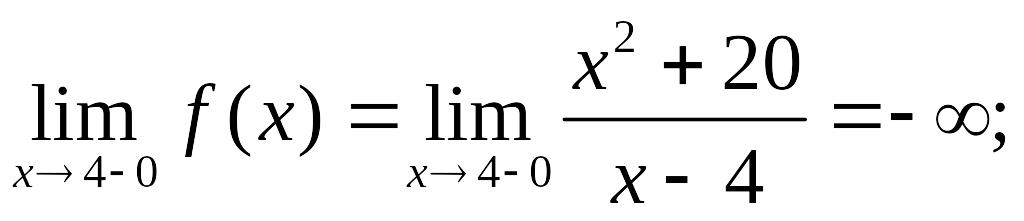
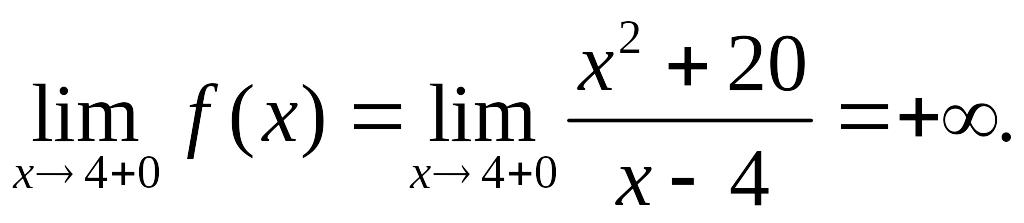
Таким образом, точка х = 4 является для заданной функции точкой разрыва второго рода, а прямая х = 4 – вертикальной асимптотой графика.

3. Исследование на экстремум и промежутки монотонности.

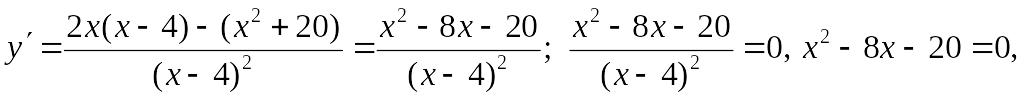
х₁ = – 2, х₂ = 10.

x	(-∞, -2)	-2	(-2, 4)	4	(4, 10)	10	(10, +∞)
	+	0	–	не сущ.	–	0	+
f(x)		max				min

4. Исследование графика на выпуклость, вогнутость, точки перегиба.

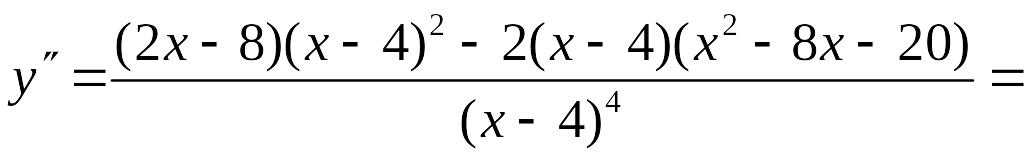
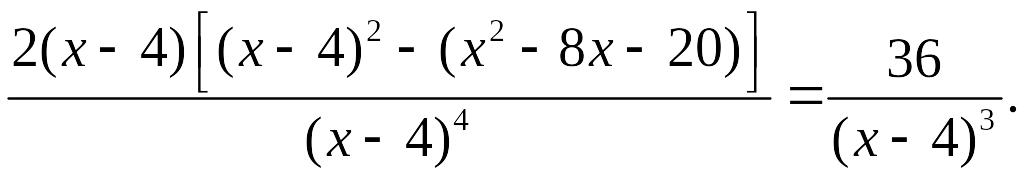
Так как , то график заданной функции точек перегиба не имеет. Остается выяснить вопрос об интервалах его выпуклости и вогнутости:

x	(– ∞, 4)	4	(4, + ∞)
	–	не сущ.	+
f(x)

5. Исследование графика на наличие наклонных асимптот.

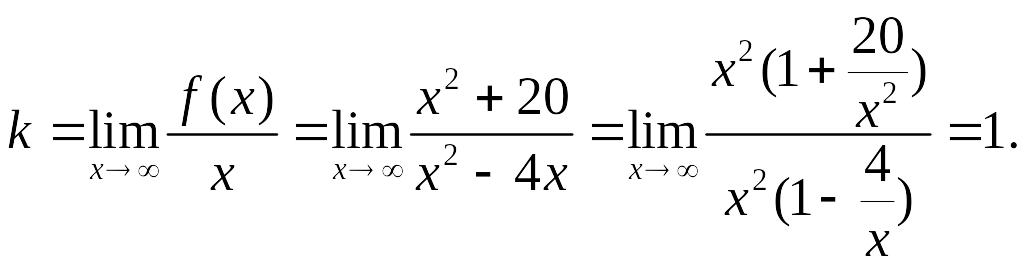
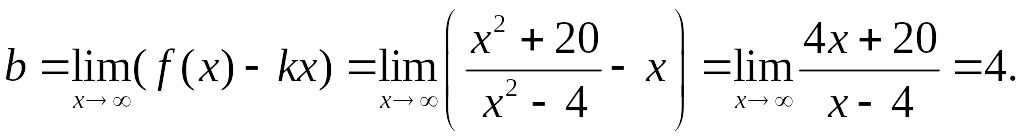
Таким образом, прямая – наклонная асимптота графика.

6. Построение графика.

Очевидно, график заданной функции пересекает ось Оу в точке (0; –5) и на основе обобщения результатов всех предыдущих исследований имеет вид:

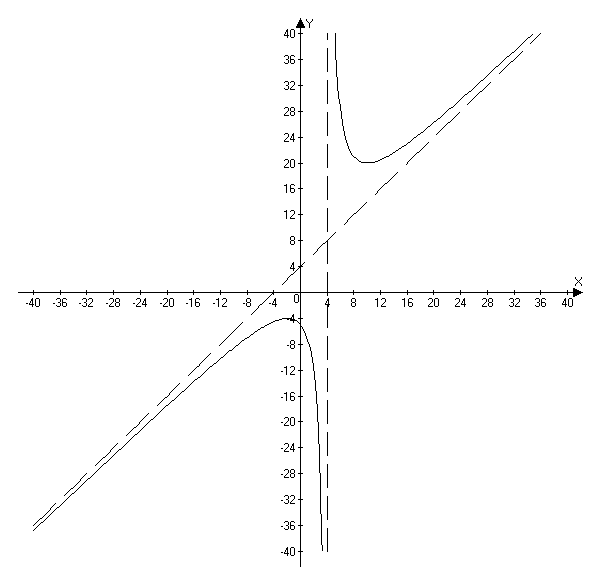
Задания для самостоятельного решения

1.	2.
3.	4.
5.	6.
7.	8.
9.	10.
11.	12.
13.	14.
15.	16.
17.	18.
19.	20.
21.	22.
23.	24.
25.	26.
27.	28.
29.	30.

Задача 2

1.Требуется изготовить цилиндрический сосуд, открытый сверху, максимальной вместимости. Каковы должны быть размеры сосуда (радиус R и высота Н), если на его изготовление имеется S=27 материала.

2.Требуется вырыть яму конической формы (воронку) с образующей, а=3м. При какой глубине объем воронки будет наибольший?

3.Найти высоту цилиндра наибольшего объема, который можно вписать в шар радиуса R

4.В эллипс вписать прямоугольник наибольшей площади. Найти стороны этого прямоугольника, если они параллельны осям эллипса.

5.Требуется изготовить закрытый цилиндрический бак максимальной вместимости. Каковы должны быть размеры бака(радиус R и высота Н), если на его изготовление имеется S=6 материала.

6.В прямоугольной системе координат через точку М(2;3) проведена прямая, которая вместе с осями координат образует треугольник, расположенный в первой четверти. Каковы должны быть отрезки, отсекаемые прямой на осях координат, чтобы площадь треугольника была наименьшей.

7.Резервуар открытый сверху, имеет форму прямоугольного параллепипеда с квадратным основанием. Каковы должны быть размеры резервуара, чтобы на его изготовление пошло наименьшее количество материала, если он должен вмещать 256 л воды.

8.Требуется вырыть яму цилиндрической формы с круглым основанием и вертикальной боковой поверхностью заданного объема V=8 . Каковы должны быть размеры ямы (радиус R и высота Н) чтобы на облицовку ее дна и боковой поверхности пошло наименьшее количество материала?

9.Из круглого бревна радиуса R= требуется вырезать балку прямоугольного сечения с основанием b и высотой h. Прочность балки пропорциональна . При каких значениях b и h прочность балки наибольшая?

10.Требуется изготовить закрытый цилиндрический бак заданного объема . Каковы должны быть размеры бака (радиус R и высота Н), чтобы на его изготовление пошло наименьшее количество материала?

11.Из бревна имеющего форму усеченного конуса, надо вырезать балку, поперечное сечение которого есть квадрат, а ось совпадает с осью бревна. Найти размеры балки (сторона квадрата а и длина балки b), при которых объем балки будет наибольшим.

12.Требуется изготовить палатку в форме правильной 4-угольной пирамиды заданной боковой поверхности, . Каковы должны быть размеры палатки (сторона основания а и высота Н), чтобы вместимость палатки была наибольшей?

13.Равнобедренный треугольник, периметр которого P=12, вращается вокруг основания. Найти основание а, при котором полученное тело вращения имеет наибольший объем?

14.Цистерна имеет форму кругового цилиндра, завершенного с одной стороны полушаром. Вместимость цистерны . Найти радиус цилиндра R, при котором цистерна будет иметь наименьшую полную поверхность.

15.Сечение строительного канала имеет форму равнобокой трапеции, боковые стороны которой равны меньшему основанию. При каком угле наклона боковых сторон сечение канала будет иметь наибольшую площадь?

16.Требуется изготовить платяной шатер, имеющий форму прямого кругового конуса заданной вместимости, . Каковы должны быть размеры конуса (высота Н и радиус основания R), чтобы на шатер ушло наименьшее количество полотна?

17.Сечние тоннеля имеет форму прямоугольника, завершенного сверху полукругом. Периметр сечения, . При каком радиусе полукруга площадь сечения будет наибольшей?

18.Из прямоугольного листа жести размером 24 9 см требуется открытую сверху коробку, вырезая по углам листа равные квадраты и загибая оставшиеся боковые полосы под прямым углом. Каковы должны быть стороны вырезаемых квадратов, чтобы вместимость коробки была наибольшей?

19.Равнобедренный треугольник, вписанный в окружность радиуса R=3, вращается вокруг основания. Найти высоту треугольника h, при котором полученное тело вращения имеет наибольший объем.

20.Найти высоту конуса наибольшего объема, который можно вписать в шар радиуса R.

21.Окно имеет форму прямоугольника, завершенного полукругом. Периметр окна равен 300 см. При каких размерах сторон прямоугольника окно будет пропускать наибольшее количество света?

22.На странице книги напечатанный текст (вместе с промежутками между страницами) должен занимать 216 , верхнее и нижнее поля должны быть по 3 см, правое и левое по 2 см. Каковы должны быть размеры страницы, чтобы ее площадь была наибольшей?

23.Через точку А(2;1) провести прямую с отрицательным угловым коэффициентом так, чтобы сумма длин отрезков, отсекаемых ею на осях координат, была наименьшей.

24.Требуется поставить палатку данного объема V, имеющую форму прямого кругового конуса. Найти отношение высоты конуса к радиусу его основания, при котором на палатку уйдет наименьшее количество материала.

25.Требуется изготовить из жести ведро данного объема V цилиндрической формы без крышки. Найти высоту цилиндра и радиус его основания, при которых на ведро уйдет наименьшее количество материал.

26.Круговой сектор имеет данный периметр P. Каков должен быть радиус сектора R для того, чтобы площадь сектора была наибольшей?

27.Сосуд, представляющий собой цилиндр, заканчивающийся снизу полусферой, должен вмещать 18 л воды. Найти размеры сосуда, при которых на его изготовление пойдет наименьшее количество материала.

28.Из куска проволоки длиной L согнуть прямоугольник, чтобы его площадь была наибольшей.

29.Одна сторона прямоугольного участка земли примыкает к берегу канала, а три другие огораживаются забором. Каковы должны быть размеры этого участка, чтобы его площадь равнялась 800 , а длина забора была наименьшей?

30.Число 66 представить в виде суммы двух положительных слагаемых так, чтобы произведение этих чисел было бы наибольшим.