3. Дифракція Френеля від колового отвору і колового диска.

Поставимо на шляху сферичної світлової хвилі непрозорий екран з отвором радіусом r₀. Закріпимо екран так, щоб перпендикуляр з джерела світла S, попав у центр отвору (Рис. 1.3.5) та в точку Р.

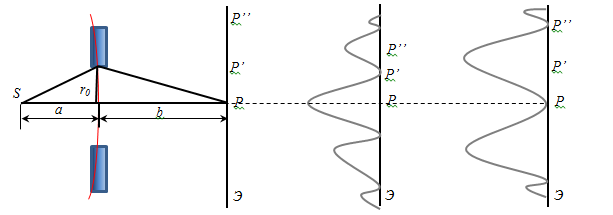
Рис. 1.3.5

(1.3.8)

де m - ціле число, то отвір залишить відкритим рівно m перших зон Френеля, побудованих для точки Р.

А число відкритих зон встановлює рівняння

m=

Тоді амплітуда буде дорівнювати

А=А₁-А₂+А₃-А₄+....А_mА/2

Перед А_m ставимо знак плюс якщо m не парне, а мінус - якщо m парне.

А= + (парне)

А= + -А_m (не парне)

Амплітуди від 2-х сусідніх зон майже однакові. Тому ( ) - А_m можно замінити на - . В результаті отримуємо:

А= ± (1.3.9)

Для малих m А_m мало відрізняється від А_1. Тому при непарних m амплітуда в точці Р майже дорівнює А₁ , а при парних = 0.

Перешкода з отвором, що відкриває непарне число зон, приводить до збільшення амплітуди майже в 2 рази, а інтенсивність - в 4 рази.

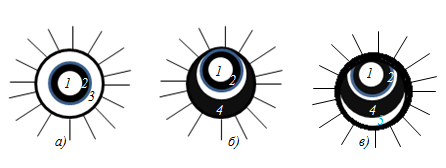
Pис. 1.3.6

Дифракційна картина

Як результат того, що отвір знаходиться симетрично до Р, S, освітленість в різних точках екрану буде залежати від r відстані до P. В цій точці, інтенсивність досягає максимума або мінімума - залежить від того, яким (парним/непарним) буде число відкритих зон Френеля.

Нехай для т. Р відкрито 3 зони Френеля (Pис. 1.3.6а). Якщо зміститься по екрану в т. Р’, то третя зона частково зачинеться і при цьому частково відкриється 4-а зона (Pис. 1.3.6б), в т. Р’ буде зменшення амплітуди. Якщо зміститься в т. Р”, то закриється частково 2-а и 3-а зони, але відкриється не тільки 4-а ще й 5-а зона (Pис. 1.3.6в), , в т. Р’’ будемо спостерігати збільшення світла. Таким чином, дифракційна картина від круглого отвору має вигляд світлих и темних кілець, причому у центрі буде світла пляма (максимум), якщо в отворі - непарне число зон, чи темне, якщо парне число зон Френеля. Якщо екран перемістити вдаль лінії SР, то на ній буде чередуватись. Якщо  m < 1, то на екрані - світла пляма. Якщо m→∞, то дифракційна картина буде спостерігатися на границі геометричної тіні.

Дифракція від колового диску

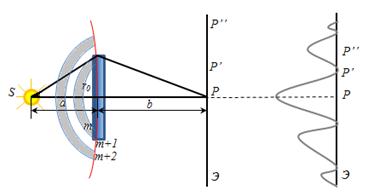
Рис. 1.3.7

Нехай диск закриває m перших зон  Френеля. Тоді амплітуда результуючого коливання в т. Р

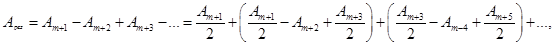(1.3.10)

згідно 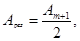    тобто в т. Р спостерігається інтерференційний максимум (світля пляма). Якщо змістити по екрану в т. Р’, то закриється частина (m+1)-й зони, але відкриється частина (m+2)-й зони. Отже, в т. Р’ буде мінімум (темне кільце). При зсуву в т. Р” перекриється частина (m+2)-й зони та одночасно відкриється частина (m+3)-й зони, і в т. Р" буде максимум. Таким чином, дифракційна картина на круглому дискові має вигляд чергующих світлих и темних кілець. У центрі картини завжди знаходиться світла пляма.

Якщо m < 1, то диск не дає геометричної тіні – освітленність екрану однакова. Якщо m→∞, то дифракційна картина спостерігається на границі геометричної тіні, а в т. Р практично темна пляма, оскільки.  . Переміщення екрану вздовж лінії SР не змінює картину на екрані.