2. Оптична різниця ходу. Умови інтерференційних максимумів і мінімумів.

Нехай розділення на дві когерентні хвилі відбувається у точці О. У точці Р відбувається накладення променів.

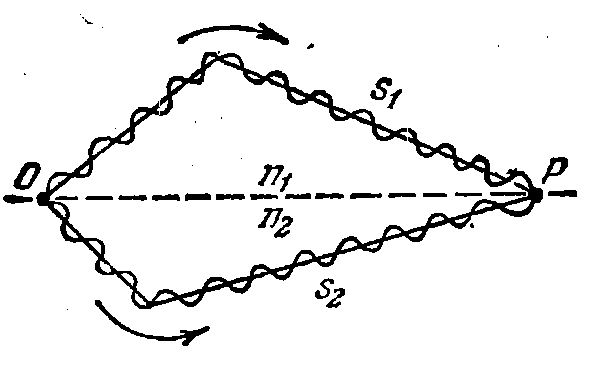
Рис. 1.2.3

Геометрична довжина шляху світла S₁ і S₂. Фаза коливань світлової хвилі в точці 0 дорівнює ωt. Запишемо рівняння для світлових коливань для точки Р: Е₁=А₁соsω(t-S₁/V₁),

Е₂=А₂ соsω(t-S₂/V₂), (1.2.7)

S₁/V₁ – час, за який пройде промінь від точки 0 до точки Р. Світлові коливання відбуваються в тому самому напрямку: Е₁ і Е₂ – однаково направленні.

Різниця фаз σ, створених двома світловими хвилями в точці Р:

σ = ω

Врахуємо формулу n=с/V. Тоді:

Замінимо, ω/с через 2πʋ/c=2π/λ₀, де λ₀ – довжина світлової хвилі у вакуумі. Для двох хвиль вона однакова. Тоді отримаємо:

σ = (n₂S₂-n₁S₁).

Δ – величина, яка чисельно дорівнює різниці оптичних довжин шляху, що проходять хвилі, називається оптичною різницю ходу двох світлових хвиль:

Δ= (n₂S₂-n₁S₁)=L₁-L₂ (1.2.8)

Тоді попередні рівняння перепишемо у вигляді:

(1.2.9)

– зв'язок між оптичною різницею ходу і різницею фаз.

Δ = ± mλ₀, (m=0;1;2...) (1.2.10)

якщо різниця фаз буде кратна цілому числу 2π: σ = ± 2πm, то хвилі, що накладаються, будуть в однаковій фазі. Таким чином, формула (1.2.10) визначає різницю ходу променів, за якої ми спостерігатимемо максимум інтерференції – умова максимуму інтерференції. Розглянемо інший випадок:

Δ = ± (m+1/2)λ₀ (1.2.11)

σ = ± (2m+1)π, (де m=0;1;2...)

У цьому випадку хвилі будуть знаходиться у проти фазі. Формула (1.2.11) – умова мінімуму інтерференції.

Розглянемо два джерела когерентних хвиль. Це дві нитки, що світяться, перпендикулярні до площини малюнка, чи щілини, через які проходить світло (Рис. 1.2.4).

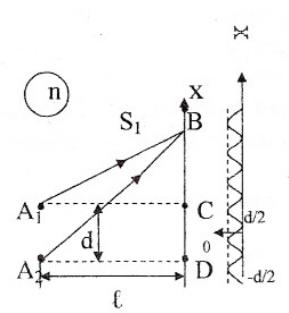
Рис. 1.2.4

Джерела А₁ і А₂ - когерентні. Виходячи з малюнка, спробуємо знайти довжину променів за теоремою Піфагора: з ΔА₁ВС: S₁²=l²+(х–d/2)².

З ΔА₂ВD: S₂²=l²+(х+d/2)².

S₂²–S₁²=l²+х²+xd+d²/4–l²–х²+xd–d²/4=2xd. Перепишемо ліву частину, враховуючи формулу для різниці квадратів: (S₁+S₂)(S₂–S₁)=2хd.

Врахуємо що:

xd<<l (1.2.12)

– це умова для спостереження інтерференції.

Тоді S₁+S₂ ≈ 21. З урахуванням цього одержуємо:

- геометрична різниця ходу променів.

Знайдемо оптичну різницю ходу. Усе це знаходиться в однорідному середовищі з показником заломлення п. Тоді, якщо це було б повітря, то відношення хd/l було би не тільки геометричною різницею ходу, але й оптичною.

.

Врахуємо формулу (1.2.10) для максимумів і одержимо:

З цього рівняння знайдемо координати максимумів:

(1.2.13)

де λ=λ₀/n, λ₀ – довжина хвилі у вакуумі.

Використовуючи рівняння (1.2.11) одержимо координати мінімумів:

(m=0;1;2...) (1.2.14)

Відстань між двома сусідніми максимумами будемо називати відстанню між інтерференційними смугами. Відстань між двома сусідніми мінімумами назвемо шириною інтерференційної смуги.

З формул (1.2.13) і (1.2.14) випливає, що відстані між сусідніми інтерференційними смугами і ширина інтерференційної смуги будуть рівні одна одній і будуть визначатися наступною формулою:

(1.2.15)