4.Закони лінійної оптики. Геометрична оптика

Розділ оптики, де світлова хвиля замінюється променями, називається геометричною чи променевою оптикою. (Рис. 1.1.4 а, б, в)

Основні закони лінійної оптики:

• Закон прямолінійного поширення світла - в однорідному середовищі світло поширюється прямолінійно.

• Закон незалежності світлових променів - промені при перетинанні не збурюють один одного.

Промені 1 і 2 не збурюють один одного, тобто, якщо прийняти один із променів, то малюнок на екрані не буде залежити від цього. Дійсно це у випадку, якщо інтенсивність світла не дуже висока. (Рис. 1.1.4а)

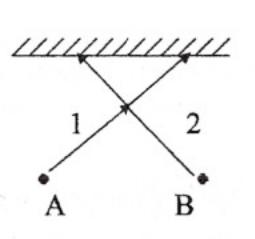
Рис. 1.1.4а

• Закон відбиття світла - відбите світло лежить в одній площині з падаючим променем і нормаллю, встановленою в точці падіння. Кут відбиття дорівнює куту падіння. (Рис. 1.1.4б)

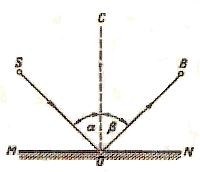
Рис. 1.1.4б

S - падаючий промінь,

B - відбитий промінь,

- кут падіння,

- кут відбиття.

• Закон заломлення світла - заломлений промінь лежить в одній площині з падаючим променем і нормаллю, встановленою в точці падіння.

(Рис. 1.1.4в)

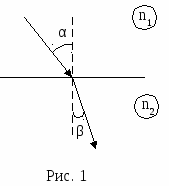
Рис. 1.1.4в

Відношення sin кута падіння до sin кута заломлення є величина постійна для даних речовин, - кут заломлення, - кут падіння.

(1.1.24)

n₁₂ - відносний показник заломлення другого середовища по відношенню до першого.

n₁₂ =V₁/V₂ - відношення фазової швидкості в першому середовищі до фазової швидкості в другому середовищі.

Можна одержати цю формулу з принципу Гюйгенса.

Принцип Гюйгенса: кожна точка, до якої доходить світлове збудження, є джерелом вторинних хвиль; поверхня, що огинає в деякий момент часу ці вторинні хвилі, указує положення до цього моменту фронту дійсно поширюваної хвилі.

Оскільки V = , то для n₁₂ отримаємо:

n₁₂ = (1.1.25)

- відносний показник заломлення двох середовищ дорівнює відношенню їхніх абсолютних показників заломлення.

Принцип Ферма: світло поширюється по такому шляху, на проходження якого йому потрібно мінімальний час.

Уявімо, що середовище неоднорідне.

dt = , V - швидкість світла.

n = c/V, тоді dt = , n - показник заломлення світла.

L = (1.1.26)

де L - оптична довжина світла.

Для однорідного середовища зв'язок між оптичною довжиною шляху L і геометричною довжиною S:

L = nS, (1.1.27)

= L/c (1.1.28)

де - час, за яке світло переміститься від 1 до 2.

З урахуванням формули (1.1.28) принцип Ферма можна перефразувати: світло поширюється по такому шляху оптична довжина якого мінімальна.

Сучасне формулювання принципу Ферма: в оптично неоднорідному середовищі світло поширюється по такому шляху оптична довжина якого екстремальна (або мінімум, або максимум, або довжина однакова для всіх можливих оптичних шляхів).

(1.1.29)

математичний запис принципу Ферма.

Доведемо закон відбиття світла (Рис. 1.1.5 а,б )за принципом Ферма.

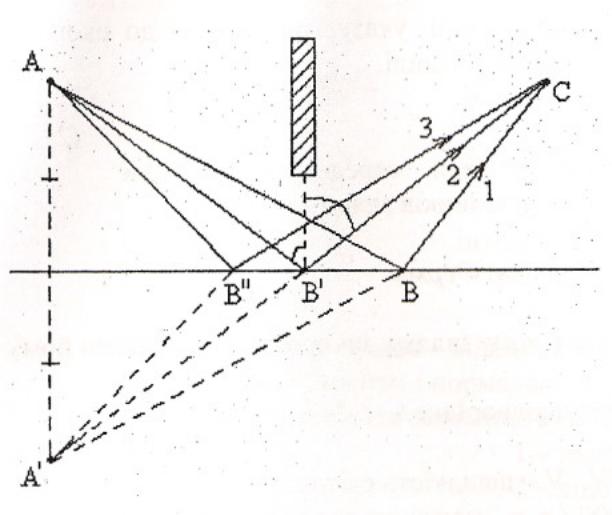
Рис. 1.1.5а

АВ"=В”А'

АВ=ВА'

АВ'=В'А'

А'ВС=АВ+ВС

А'В"С=АВ''С

АВ'С=А'В'С

АВС - найкоротший шлях.

Усі ці промені будуть мати однакову оптичну довжину шляху і будуть називатися таутохроними променями. Це екстремальний випадок, коли довжини шляхів однакові.

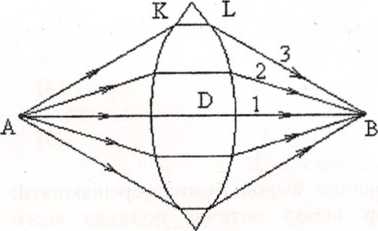
Рис. 1.1.5б

Контрольні питання

1. Електромагнітна природа світла.

2. Розділи оптики.

3. Хвильове рівняння. Плоска електромагнітна хвиля.

4. Фотометрія. Фотоелектричні поняття й одиниці: світловий потік, сила світла, світність, освітленість.

5. Сформулювати закони лінійної оптики.

6. Принцип Гюйгенса.

7. Принцип Ферма. Навести аналітичний вираз.

Література:

1. Навчальний посібник для студентів вищих технічних і педагогічних закладів освіти / Кучерук І. М., Горбачук І. Т.; за ред. Кучерука І. М. - К.: Техніка, 1999.Том 3: Оптика. Квантова фізика. - 520 с

2. Курс общей физики. Т.2. Электричество и магнетизм. Волны. Оптика. Савельев И.В. 2-е изд., перераб. - М.: Наука, Гл. ред. физ-мат. лит., 1982.— 496с.

3. Общий курс физики. В 5 т. Том IV. Оптика.   Сивухин Д.В.3-е изд., стереот. — М.: Физматлит, 2005. - 792 с.

Лекція 2

тема: "Інтерференція світла"

Рекомендований до перегляду відеоматеріал перед ознайомленням з лекційним матеріалом:

1. http://www.youtube.com/watch?v=aJdpJplUDOQ

2. http://www.youtube.com/watch?v=1ia91cdbhQk

Питання лекції:

1. Інтерференція світлових хвиль і умови її спостереження

2. Оптична різниця ходу. Умови інтерференційних максимумів і мінімумів.

3. Способи спостереження інтерференції світла.

4. Інтерференція світла в тонких плівках.

5. Практичне використання інтерференції. Інтерферометри. Інтерферометр Майкельсона.

6. Додаток. Нерелятивістський ефект Доплера

1. Інтерференція світлових хвиль і умови її спостереження

Розглянемо дві світлові хвилі з однаковою частотою ω, у яких коливання векторів Е і Н проходять в одному напрямку.

Е₁= A₁cos(ωt + α₁), (1.2.1)

Е₂ = A₂cos (ωt + α₂). (1.2.2)

Розглянемо точку, у якій ці хвилі складаються.

А - амплітуда результуючого коливання, а α₁ і α₂ — початкові фази коливань, що складаються (Рис. 1.2.1). Визначимо її. використовуючи теорему косинусів:

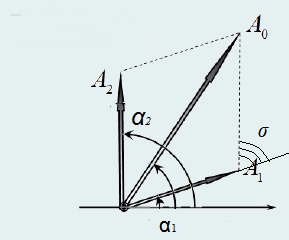
Рис. 1.2.1

А²=А₁²+А₂²+2A₁A₂cosσ, (1.2.3)

де σ - різниця початкових фаз коливань.

Уведемо поняття когерентності: якщо різниця фаз σ коливань, що збуджуються хвилями, залишається постійною в часі, то хвилі будуть називатися когерентними. Джерела цих хвиль також називаються когерентними

Когерентність – це погоджене протікання декількох коливальних і хвильових процесів.

Припустимо, що хвилі не когерентні. Тоді середнє значення різниці початкових фаз <cosσ>= 0. У формулі (1.2.3) матимемо:

<А²>=<А₁²>+<А₂²>

Оскільки інтенсивність пропорційна квадрату амплітуди: I ~ А², то будемо мати:

І=І₁+І₂ (1.2.4)

Інтенсивність світла при накладенні не когерентних хвиль дорівнює сумі інтенсивностей, що створюються кожною з хвиль окремо.

Усереднимо за часом формулу (1.2.3) для когерентних хвиль:

(1.2.5)

У випадку когерентних хвиль cosσ = <cosσ> - постійна: cosσ ≠ f(t)

У тих точках простору, для яких cosσ > 0, I буде більша за I₁ + I₂; в тих точках, для яких cosσ < 0, I буде менша за I₁ + I_2.

При накладенні когерентних світлових хвиль відбувається перерозподіл світлового потоку в просторі. У результаті цього в одних місцях виникають максимуми, а в інших - мінімуми інтенсивності. Це явище називається інтерференцією хвиль.

Якщо І₁=І₂, тоді згідно (1.2.5), результуюча інтенсивність у точках, для яких різниця фаз дорівнює σ, визначається формулою (1.2.6):

І=2I₀(1+соsσ)=4І₀cos² (1.2.6)

У місцях мінімумів інтенсивності результуюча інтенсивність дорівнює нулю, у місцях максимумів I_max=4І₀.

Особливо чітко інтерференція проявляється в тому випадку, якщо інтенсивність обох хвиль однакова (I₁ = I₂) тоді в мінімумах I = 0, а в максимумах 4I₁. У випадку некогерентних хвиль за умови I₁ = I₂ виходить, що освітленість всюди I=2I₁.

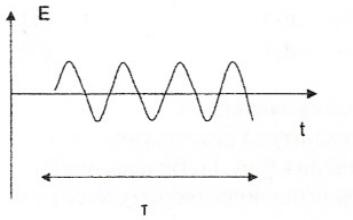
Рис. 1.2.2

Звичайні джерела світла не є когерентними, тому що кожен атом речовини, що випромінює світло, випускає світло у вигляді цугу – світлового імпульсу (Рис. 1.2.2). Довжина цугу в просторі l=cτ, де с = 3•10⁸ м/с, а τ ~ 10^-8с, час когерентності. Звичайно l ~ (1÷10)м.