
- •1. Плоска електромагнітна хвиля. Енергія електромагнітних хвиль.
- •1. Плоска електромагнітна хвиля
- •2. Світлова хвиля. Хвильова оптика
- •3. Фотоелектричні поняття й одиниці
- •4.Закони лінійної оптики. Геометрична оптика
- •2. Оптична різниця ходу. Умови інтерференційних максимумів і мінімумів.
- •3. Способи спостереження інтерференції світла.
- •4. Інтерференція світла в тонких плівках
- •6. Додаток. Нерелятивістський ефект Доплера
- •2. Принцип Гюйгенса-Френеля. Зони Френеля
- •3. Дифракція Френеля від колового отвору і колового диска.
- •4. Дифракція Фраунгофера від щілини
- •5. Дифракційні ґратки
- •6. Дифракція рентгенівського випромінювання
- •6. Голографія
- •Дифракція рентгенівського випромінювання?
- •Поляризація при відбитті та заломленні світла на межі двох діелектриків
- •Поляризація при подвійному променезаломлення
- •Поляризаційні пристрої
- •Кристалічна пластина між двома поляризаторами
- •Штучне подвійне променезаломлення
- •Обертання площини поляризації
- •Штучне подвійне променезаломлення.
- •Нормальна і аномальна дисперсія. Групова швидкість
- •Електронна теорія дисперсії світла
- •Поглинання світла
- •Розсіювання світла
- •Ефект Вавілова-Черенкова
- •Розсіювання світла.
- •Ефект Вавілова-Черенкова.
- •Визначення поглинальної здатності тіла :
- •Закон Кіргофа
- •Закон Стефана-Больцмана
- •Закон зміщення Віна
- •Поняття рівноважного випромінювання
- •Формула Релея-Джинса
- •Формула Планка
- •2. Фотоефект
- •3. Фотони. Дослід Боте
- •4. Тиск світла
- •5. Ефект Комптона
- •6. Межі застосування класичної теорії
- •Тиск світла.
- •Ефект Комптона.
5. Ефект Комптона
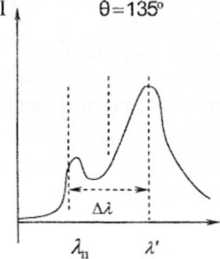
Комптоном (1923) вивчалось розсіяння рентгенівського випромінювання різними речовинами. З’ясувалося, що в розсіяному випромінюванні спектральних ліній, які відповідають довжині хвилі λп (падаючих рентгенівських променів), присутні лінії, довжина хвилі яких λ > λп. При цьому виявилось, що зміна довжини хвилі ∆λ = λ͗ - λп не залежить від λп, падаючої хвилі та роду речовини, що розсіює, а лише від кута θ між напрямом падаючої хвилі і напрямом розсіяння.
Експериментальне значення ∆λ:
∆λ=2Λ0 sin(θ/2), (2.2.11)
де Λ0 - стала, яка має назву “ комптонівська довжина хвилі ”:
Λ0=![]()
де т - маса мікрочастинки, що розсіює рентгенівське випромінювання.
Графік інтенсивності розсіяного випромінювання I від λ для різних кутів розсіяння подано на Рис. 2.2.8.
I Спектр падаючої хвилі
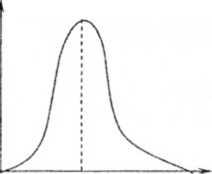
λ
θ=450
Особливості розсіяння можна пояснити, якщо розглядати цей процес як акт пружного зіткнення рентгенівських фотонів з практично вільними електронами речовини. Застосуємо для опису закону збереження енергії та імпульсу для абсолютно пружного удару. θ=450
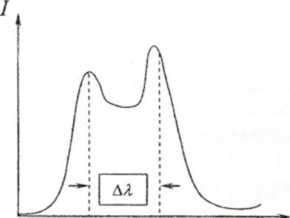
λп λ λ
Фотон:
енергія до взаємодії: ф= ɷ =
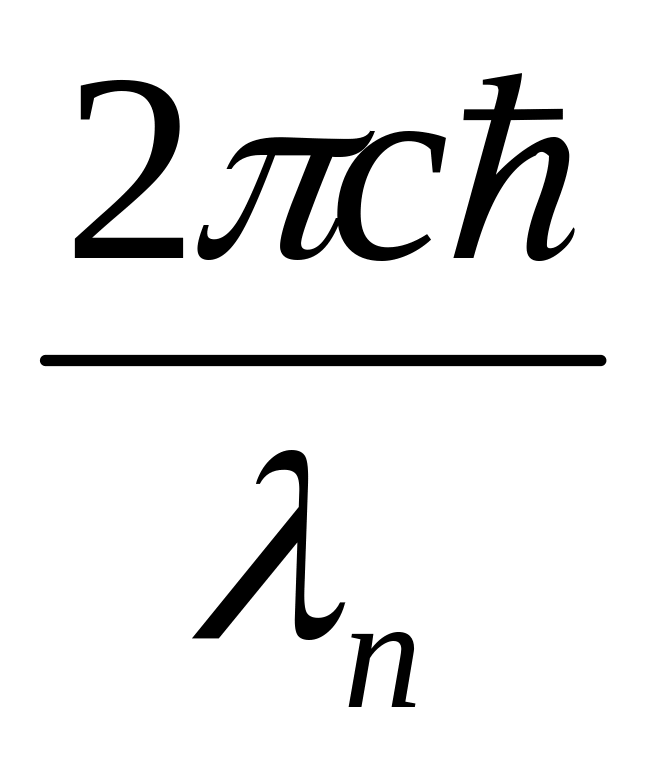 ;
;
імпульс: рф= k; р=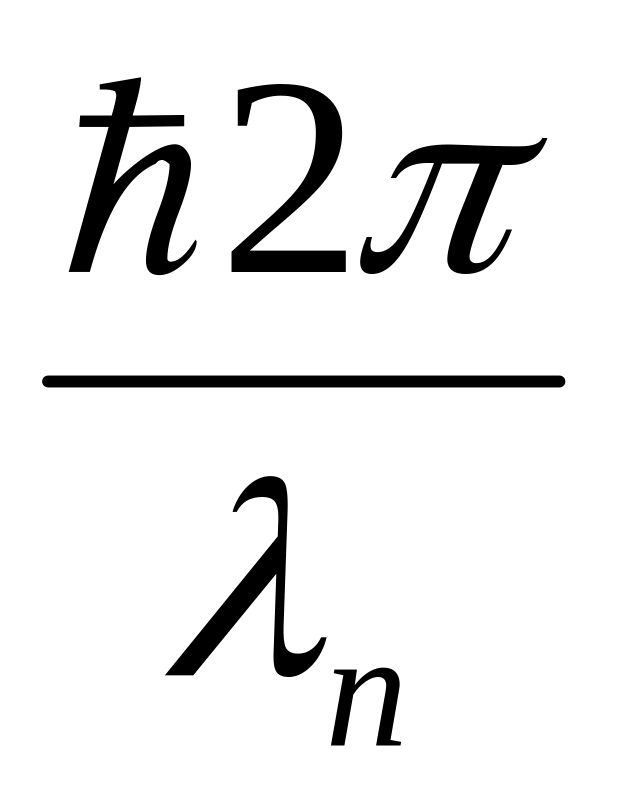 ;
;енергія після взаємодії (енергія розсіяного фотона):
ф`
=
ɷ`
=![]() ;
;
імпульс розсіяного фотона: р = k
 λ
λ
Рис. 2.2.8
Електрон:
енергія до взаємодії: = mc2 ;
імпульс: р = 0;
енергія після взаємодії: `=
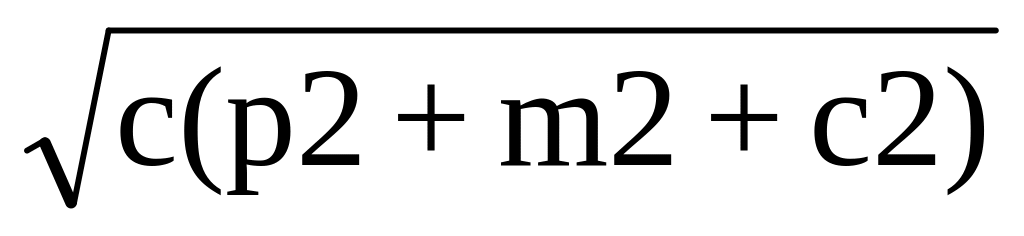 ;
;
імпульс: р = mV ; (Рис. 2.2.9)
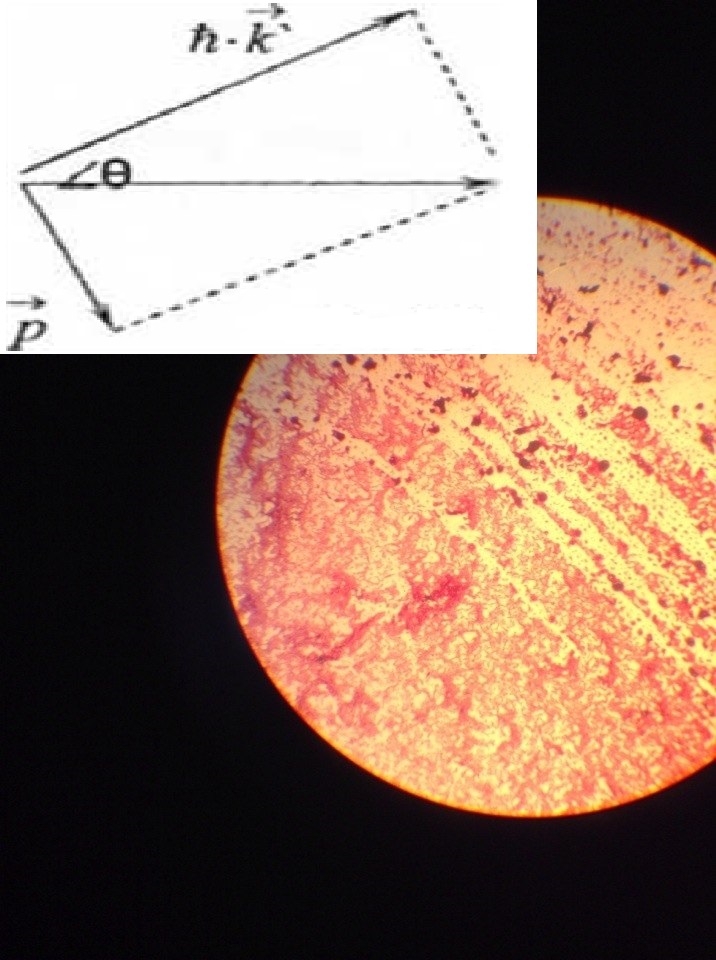
Рис. 2.2.9
Закони збереження запишемо так:
енергії: ɷ + mc2 = ɷ` + c2
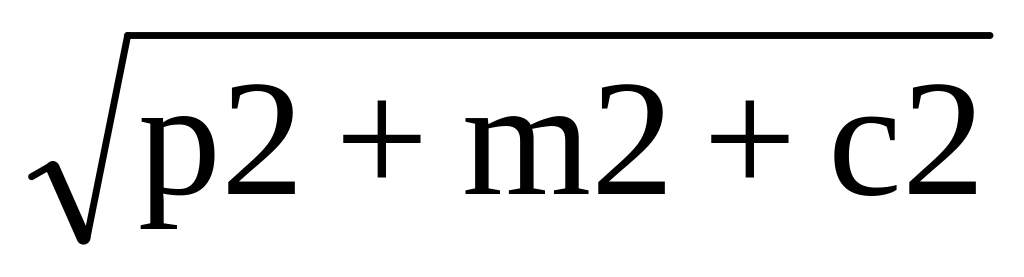 (2.2.12)
(2.2.12)імпульсу: k = k` + p. Розв'язок системи рівнянь (2.2.12) дає:
∆λ
= λ͗ - λп
=
![]() (1- cos
θ) = Λ0
(1- cos
θ) = Λ0![]() 2(θ/2);
2(θ/2);
що співпадає з експериментальними даними (2.2.11).
Цим ефект Комптона підтверджує фотонну теорії випромінювання та доводить правомірність застосування законів збереження енергії та імпульсу при взаємодії електрона і фотона як взаємодії корпускул (часточок).
Основний висновок частини 1 “ Квантова оптика ”: у цьому розділі наведено експериментальні дослідження та теоретичні міркування, що їх пояснюють, які підтверджують корпускулярно-хвильовий дуалізм випромінювання (у тому числі - світла).
6. Межі застосування класичної теорії
Розмірність сталої Планка, - кванта дії, - [ ] - Дж•с = (кг•м•с)/с2=кг(м/с)м.
Таку саму розмірність має фізична величина - момент імпульсу (момент кількості руху):
L = [r•p] => [L] = кг(м/с)м
Критерії правомірності застосування класичної механіки ґрунтується на співставленні цих двох фізичних величин, і L : якщо у даній фізичній системі чисельне значення деякої природної динамічної змінної з розмірністю кванта дії - сталої Планка, - є порівняння з самою сталою , то поведінка такої системи описується у рамках квантової механіки. Якщо змінні, що мають розмірність кванта дії, є великими у порівнянні з чисельним значенням , то системи з достатньою точністю описується законами класичної механіки.
Приклади.
Для оцінки параметрів розглянемо рух електрона у двох ситуаціях: (а) - в електронно-променевій трубці; (б) - на орбіті атома водню.
Підрахунки.
(а)
Lа
= [r•p];
r
трубку
візьмемо порядку 10 см; якщо прискорюється
напруга U=104В,
то р=
![]() =
(2•9,1•10-31•1,6•10-19•104)^0,5
= 5•10-22
кг(м2/с);
=
(2•9,1•10-31•1,6•10-19•104)^0,5
= 5•10-22
кг(м2/с);
Lа = 5•10-22•0,1 =5•10-23 кг(м2/с), де m i e - маса і заряд електрона, р - його імпульс.
(б) Lб = [r•p]; r = 5•10-22; V=5•106 (м/с); Lб =5•10-22•9,11•10-31•106=4,5•10-35.
Бачимо,
що у випадку (а)
![]() =
1011,
тобто момент кількості руху
=
1011,
тобто момент кількості руху
електрона
за порядком величини багато більший за
сталу Планка, а у випадку (б)
![]() = 0,1 -
L
на порядок менше, отже використання
класичної теорії не правомірне.
= 0,1 -
L
на порядок менше, отже використання
класичної теорії не правомірне.
Контрольні питання
