5. Дифракційні ґратки

Ґратка – це пластина, що містить N паралельних щілин (штрихів) однакової ширини b і відстанню між щілинами d; d називається – період ґратки. З рис 10 випливає, що

Δ=CD=dsinφ

– це різниця фаз Δ для променів 1 і 2 , тобто, для довільних сусідніх променів. Будемо пам'ятати, що між променями щілини можлива інтерференція. Умова (1.3.24) може бути застосована і до дифракційних ґраток.

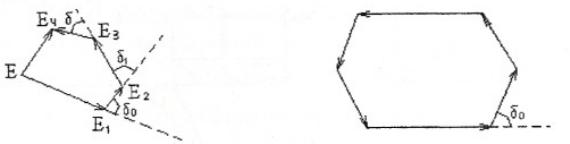
Рис. 1.3.11

δ= =( )dsinφ (1.3.26)

– різниця фаз між відповідними променями двох сусідніх щілин. На Рис. 1.3. 11, E_i коливання, що йде від і-ї щілини, Е – результуюче коливання. Е=0, відповідає min. Це буде у випадку коли амплітуди світлових коливань, що додаються, утворюють правильний N-кутник (Рис. 1.3.11). δ₀ – зовнішній кут правильного N-кутника:

δ₀= (1.3.27)

δ=δ₀k= (1.3.28)

де k ціле число не кратне N.

Прирівнюємо (1.3.26) і (1.3.28)

( )dsinφ=

dsinφ=± (1.3.29)

– умова додаткових мінімумів, k=1,2,..., N-1, N+1, …, 2N-1, 2N+1,...

Якщо k=N, або кратне N, то відразу одержимо умову (1.3.24), чого не повинно бути, якщо розглядаються ґратки.

dsinφ=±mλ (1.3.30)

– умова головних максимумів, т=0, 1, 2,...

bsinφ=±mλ (1.3.31)

– умова колишніх мінімумів, n=1, 2, 3,...

З (1.3.30) і (1.3.31) випливає, що між двома головними максимумами розташовується (N-1) додатковий мінімум:

dsinφ=mλ+ , P=1, 2, …, N-1.

Врахуємо, що кутова відстань між головним максимумом і додатковим мінімумом буде: δ(dsinφ)=λ/N, dcos(φ)δφ=λ/N, δ – диференціал кута.

Звідки маємо:

δφ=

– відстань між максимумом і додатковим мінімумом.

Різкість головного максимуму, вона ж є кутовою шириною головного максимуму при cosφ≈1, буде дорівнювати:

δφ= (1.3.32)

При заданому періоді d ґратки різкість головного максимуму зростає, а кутова ширина убуває зі зростанням числа щілин (штрихів) дифракційної ґратки.

Запишемо амплітуду світлової хвилі, що дифрагує під кутом φ у дифракційній гратці (А – задається на екрані):

A=|A₀( )( )|, α= , β= , (1.3.33)

де d – період гратки.

Вираз (sinNβ)/β дорівнює N, якщо для φ взяти умови головних максимумів (1.3.25): dsinφ=±mλ.

Підносимо праву і ліву частину (1.3.33) у квадрат і врахуємо, що А²=I – інтенсивність, а А₀²N²=І₀ – інтенсивність світлової хвилі, яка не відхиляється від початкового напрямку і йде уздовж головної оптичної осі лінзи:

І=I₀ (1.3.34)

Отже, для напрямків, які визначаються умовою (1.3.30), коливання від окремих щілин взаємно підсилюють одне одного, унаслідок чого амплітуда результуючого коливання у відповідній точці екрану збільшується в N разів, а інтенсивність в N²: І_max=N²I_φ. При великій кількості щілин світло, що пройде крізь гратку, збирається в окремих різко обкреслених ділянках екрана. Положення максимів на цих ділянках визначається умовою (1.3.30).