1. Найти предложенную нагрузку.

2. Создать диаграмму переходов состояний для системы, где состояние обозначает число клиентов в системе и фазу обслуживающего прибора.

3. Найти среднее время ожидания для произвольного вызова и среднее время ожидания вызова, который поставлен на ожидание.

4. Найти среднюю величину временного интервала, который проходит в случайный момент времени, пока не будет обслужен клиент с очень высоким приоритетом (дисциплина очереди — без приоритета).

5. Найдите производящую функцию (или функцию распределения) и среднюю величину и дисперсию числа заявок от клиентов, которые прибывают в течение времени обслуживания.

6. Предположим, что все заявки от клиентов имеют вышеупомянутое распределение времени обслуживания, и выберем среднее время обслуживания как единицу времени. Рассмотрим систему организации очереди с двумя классами и предложенной нагрузкой, равной 0.4 Эрл на каждый класс. Один из классов имеет более высокий приоритет. Найдите среднее время ожидания для клиентов в каждом из двух классов, когда дисциплина организации очереди:

1. неприоритетная,

2. приоритетное возвращение к работе.

Упражнение 13.7. М/н2/1 система организации очереди с совместным использованием процессора

Заявки прибывают в компьютерную систему согласно Пуассоновскому процессу с интенсивностью X.

Время обслуживания имеет гиперэкспоненциальное распределение с двумя фазами, обозначенными а и соответственно Ь:

F(t) = р(\ - е~+ -р){\ -e-W).

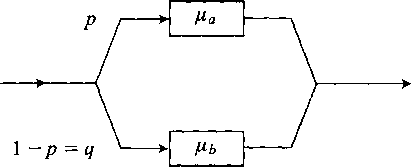
1. Найти предложенную нагрузку А.

Далее мы принимаем, что А <1. Компьютерная система работает как система с одним обслуживающим прибором (процессор), использующим совместную дисциплину организации очереди, то есть если в системе есть х заявок, то работа в фазе а обслуживается со скоростью ^„/_х и работа в фазе Ь обслуживается со скоростью ^>/_х. Состояние системы определяется (г, у), где / - число заявок в фазе a,aj- число вакансий в фазе Ь. Диаграмма пере­ходов состояний будет двухмерной со структурой, показанной на рисунке.

2. Найти отсутствующую интенсивность в соединении с состоянием:

1. , (1,2), (2,2) и (2,1).

3. Показать, рассматривая вышеупомянутые четыре состояния, что диаграмма переходов состояний обратима. М/М/1 -система организа­ции очереди с предложенной нагрузкой (при А<1) имеет вероятности состояния равновесия:

р(1)=р(0)'А\ i = 0,1,2,...

4. Показать, выражая вероятности состояния через состояниер(0; 0), что вышеупомянутая система М/Н2/Х, где процессор совместно исполь­зует систему, имеет те же самые вероятности состояний, что и М/М/1, когда мы предполагаем, что:

i

p(i) = ^ р(х, i — х), i = 0, 1, 2,... ,

х-0

и рассматриваем только / = 1 и 2.

Упражнение 13.8. Циклическая система организации очереди

Мы рассматриваем следующую циклическую систему организации очереди.

Шесть заявок циркулируют в системе и обслуживаются альтернатив­но в центральном процессоре (экспоненциально распределенное время обслуживания со средней величиной ц^-1 = Vi единицы времени) и в один из двух каналов ввода/вывода (полная доступность, экспоненциально рас­пределенное время обслуживания со средней величиной ц~‘ = 1 единица времени). Если оба канала ввода/вывода являются свободными, заявка выбирает канал случайным образом.

Каналы ввода-вывода Центральный процессор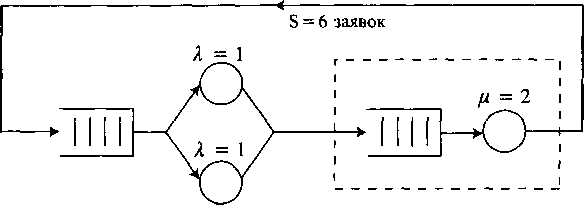

Состояние системы определяется как число заявок, которые обслу­живаются или ждут в очереди в центральном процессоре (соответ­ствует числу заявок в блоке «Центральный процессор» на рисунке). Предполагается, что система находится в статистическом равновесии.

1. Создать диаграмму переходов состояний системы и найти вероятно­сти состояния.

2. Найти использование центрального процессора и каждого из двух каналов ввода-вывода.

3. Вычислить среднюю длину очереди в каждой из двух систем органи­зации очереди, используя вероятности состояний. Примените фор­мулу Литтла, чтобы получить полное время циркуляции для случай­ной работы. (Время циркуляции — среднее время общего количества циклов.)

Вероятности состояния, полученные в вопросе 1 — математические ожидания времени, то есть вероятности состояния в случайный момент времени.

4. Найти вероятности состояния, для заявки, которая только закончила обслуживание в «канале ввода—вывода» и поступает в систему оче­редь — центральный процессор (математическое ожидание вызова). Затем вычислите вероятность, что заявка будет ожидать обслужива­ния (положительное время ожидания) в Центральном процессоре, соответственно в каналах ввода-вывода.

Найдите средние времена ожидания для задержанного вызова в цен­тральном процессоре, соответственно в канале ввода-вывода.

5. Вычислите вероятность состояния, используя алгоритм свертывания для сети очередей.

Упражнение 13.19. «Дырявое ведро»: система организации очереди M/D/1/2

Основные положения

«Дырявое ведро» — механизм для управления ячейкой (пакетом) в ходе поступления вызовов в процессе соединения в СИСТЕМЕ ATM. Механизм соответствует системе организации очереди с постоянным вре­менем обслуживания (длина ячейки =53 байта) и ограниченным буфером. Если процесс поступления вызовов — Пуассоновский процесс, то мы имеем Л/Д)//Д-систему. Размер утечки из «ведра» соответствует средней интен­сивности поступления заявок, принимаемых за достаточно длительный период, тогда как размер «ведра» (буфер) обозначает избыток, разрешен­ный в течение короткого временного интервала. В системе ATM механизм работает как виртуальная система организации очереди, где ячейка либо принимается немедленно, либо отклоняется. Счетчик указывает значение функции нагрузки. Контракт между оператором (сеть) и пользователем (соединение) согласовывает размер утечки и «ведра» и основан на инфор­мации о том, какое качество обслуживания способна гарантировать сеть.

Упражнение

Сначала рассмотрим систему организации очереди М/D/l, в кото­рой примем Пуассоновский поток вызовов с интенсивностью X = 0,6931 вызова в единицу времени, постоянное время обслуживания, которое мы выбираем как единицу времени, и один сервер. Число мест ожидания неограниченно, и система находится в статистическом равновесии.

1. Найти первые вероятности состояния р(0), р(\) и р(2) (заметьте, что е⁰'⁶⁹³¹ =2). Мы принимаем, что есть только одно место ожидания (М/D/l/ 2).

2. Найти от вероятности состояний в вопросе 1, применяя формулу Кейлсона (Keilson) в секции 13.3.4, вероятности состояния q(Q), q( 1) или q(2) в конечной системе.

3. Какова вероятность, что вызов будет:

1. обслужен немедленно?

2. задержан перед обслуживанием?

3. отклонен?

4. Найти, используя теорему Литла, среднее время ожидания для ожи­дающих в очереди клиентов (при положительном значении время ожидания).

1Найти предложенную нагрузку для обоих потоков нагрузки, изме­ренную в числе каналов.

1Составить уравнения равновесия узла для состояния (2,1). Найти (выраженные вероятностями состояний) потери по времени и поте­ри по вызовам для новых попыток вызова.