вообще. Мы должны потребовать, чтобы для некоторого положительного значения п выполнялось неравенство:

g-A {1-Е_п(А)} >с₀+ с-п. (7.36)

Рис. 7.7 показывает вероятности блокировки для некоторых зна­чений F_B. Отметим, что экономический расчет на прибыль в некотором смысле заложен в значении выигрыша. Практически мы выбираем F_B частично независимо от функции стоимости.

В Дании использовались следующие значения:

F_B-0,35 для первичных групп каналов;

F_B = 0,20 для обслуживания резервных первичных групп. (7.37);

F_B - 0,05 для групп без альтернативного маршрута.

Рисунок 7.7. Случай, когда размерность вероятности блокировки нагрузки с фиксированным значением значения выигрыша F_B для малых значений предложенной нагрузки становится большим (см. таблицу. 7.2)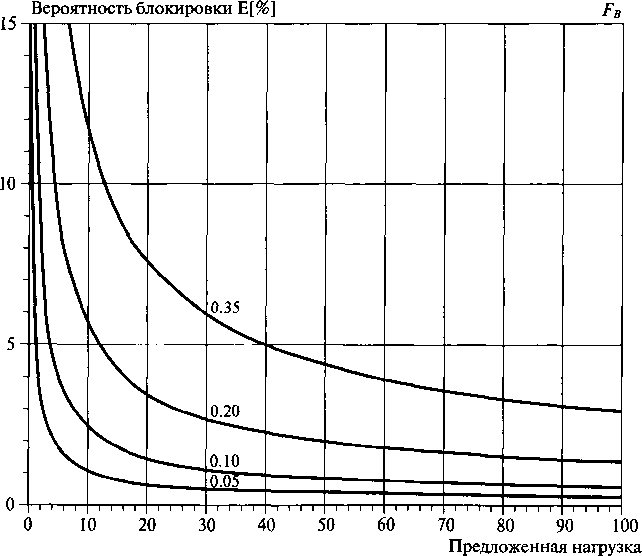

Краткие итоги

• В-формула Эрланга основана на модели, которая содержит три эле­мента: структура, стратегия и нагрузка.

• Мы рассматриваем систему из п идентичных обслуживающих при­боров (серверы, каналы, слоты), работающих параллельно.

• Вызов, достигая системы, принимается для обслуживания, если, по крайней мере, один канал свободен. Если все каналы заняты, систе­ма переполняется, и попытка вызова блокируется.

• Принимается, что времена обслуживания являются экспоненци­ально распределенными с интенсивностью д. Процесс поступления вызовов - Пуассоновский процесс со скоростью X.

• Предполагается, что предложенная нагрузка поступает при бес­конечном числе каналов.

• Самые важные показатели уровня обслуживания для систем с поте­рями - потери по времени Е, потери по вызовам В, и потери по нагрузке С.

• Состояние системы, [г], как число занятых каналов i (г = 0; 1; 2,...). Все состояния системы показаны в виде окружностей и дуг от одного состояния до другого состояния, на которых приведены значения интенсивности.

• Предполагается, что система находится в статистическом равнове­сии. В статистическом равновесии число в единицу времен переходов в состояние [/] равно числу переходов из состояния [/].

• Будущее развитие диаграммы состояний зависит только от существу­ющего состояния, а не от того, как процесс прибыл в это состояние (марковское свойство).

• Во многих случаях мы можем применять простую структуру диаграм­мы перехода состояния. Применим фиктивное сечение, например, между состоянием [/—7] и [/] (т.е. выделяем переходы от состояния [0]; [1].... [/^—Л). Затем рассматриваем в статистическое равновесие нагрузки от состояния [i~l\ к [/] и изменение от состояния [/] к [/-7].

• Число занятых каналов в случайный момент времени подчиняется Пуассоновскому распределению, число вызовов в фиксированном временном интервале также подчиняется Пуассоновскому распре­делению.

• Усеченное Пуассоновское распределение (первая формула Эрланга) - это такое распределение, для которого пространство состояний ограни­чено {0; 1,...я}.

• Потери по времени: вероятность, что все п каналов заняты в случай­ный момент времени.

Потери по вызовам: вероятность, что случайный вызов будет потерян.

Потери по нагрузке: разность между предложенной и потерянной нагрузкой.

Для всех систем с Пуассоновскими потоками вызовов эти характе­ристики равны.

• Нагрузка, которую несет /'-ый канал (использование а..), зависит от типа поиска.

• Функция увеличения обозначает увеличение обслуженной нагрузки, когда число каналов увеличено на один от п до п + 1.

• Стандартная процедура моделирования задач посредством приме­нения диаграмм перехода состояния состоит из множества шагов и может быть сформулирована в общих терминах. Эта процедура также применима для многомерных диаграмм перехода состояния.

• Для вычислений формула Эрланга не является удобной: и! увеличи­вается так быстро, что в компьютере возникает перегрузка, поэтому на практике применяется рекурсивная формула.

• Когда измеряется нагрузка системы обслуживания, мы должны обе­спечить баланс требований уровня обслуживания и экономических ограничений.

• Самый объемный показатель - Качество обслуживания (QoS). Он включает все аспекты соединения, такие, как качество речи, задерж­ка информации, потери, надежность и т.д. Уровень обслуживания (GoS) или сетевые рабочие характеристики включают аспекты, свя­занные только с емкостью сети.

• На основе работ Мо сформулированы фундаментальные принци­пы измерения нагрузки для телекоммуникационных системах как Принципы Мо.

• Общая стоимость для данного числа каналов — стоимость кабеля и убыль из-за потерянной нагрузки (упущенный доход).

Лекция 8. Полнодоступные системы с потерями

В этой лекции мы обобщаем классическую систему с потерями Эрланга и Пуассоновским процессом поступления заявок, зависящих от состояния. В частности, рассматриваются модели так называемой Д/’Р-нагрузки (ВРР — Ifinomial, Poisson, Pascal):

• Биноминальный случай: модель Энгсета,

• Пуассоновский случай: модель Эрланга, и

• Паскалевский случай (отрицательный биноминальный) случай: модель Пальма-Воллстрема.

Все эти модели не зависят от распределения времени обслужива­ния. Модели Энгсета и Паскаля не зависят также и от распределения свободного времени источников. После введения в секции 8.1 мы рас­сматриваем основную классическую теорию. В секции 8.2 рассмотрим биноминальный случай, где число источников S (абонентов, клиентов, заявителей) ограничено и число каналов п всегда достаточно (S<n). Для этой системы применяются уравнения равновесия, такие же, как и в случае Пуассоновского распределения (секция 7.2). Мы рассматриваем стратегию с явными потерями вызовов (LCC — Lost-Calls-Cleared).

В секции 8.3 пойдет разговор о случае, когда число каналов огра­ничено так, чтобы оно стало меньше, чем число источников (n<S'). Мы можем тогда рассмотреть блокировку и получим усеченное биноминаль­ное распределение, которое также названо распределением Энгсета.

Вероятность потерь по времени Е определяется формулой Энгсета. В системах с ограниченным числом источников потери по времени, поте­ри по вызовам и потери по нагрузке различаются. Их зависимость опреде­ляется теоремой поступления заявок, которая утверждает: «вероятность состояния системы, наблюдаемой клиентом (математическое ожидание по вызовам), равна вероятности состояния системы без этого клиента

о- О о- о- ООО о

S источников и каналов

Рисунок 8.1. Полнодоступная система с потерями с S источниками, которая генерирует нагрузку на и каналов. Система показана в виде так называемой chicko-граммы*. «Клюв» источника символизирует устройство выбора и указывает на каналы (обслуживающие прибо­ры), которые может выбрать источник