§8. Инверсионная симметрия энергетических зон и приведенная зона Бриллюэна.

Кривые зависимости для различных энергетических зон отличаются друг от друга, но энергия в каждой зоне n является четной функцией волнового вектора , т.е. . Действительно, рассмотрим одноэлектронное уравнение Шредингера для связанного электрона в кристалле.

(1)

, , - функция Блоха.

Наряду с уравнением (1) рассмотрим комплексно сопряженное уравнение Шредингера:

(2)

Так как и является вещественными, то знаки комплексного сопряжения можно опустить, тогда (2) принимает вид:

(3)

Функция входящая в (3) является Блоховской, потому что ей соответствует оператор , инвариантный относительно трансляции на собственные вектора

, (4)

Значит, Блоховской функции соответствует волновой вектор . Сравнивая уравнения (1) и (3) приходим к выводу, что , т.е. энергия в каждой n зоне является четной функцией волнового вектора или иными словами, каждая энергетическая зона кристалла обладает инверсионной симметрией относительно точки Г, центра первой зоны Бриллюэна. .

Следовательно, приведенный на рисунке §7 энергетический спектр электронов кристалла обладает зеркальной симметрией относительно оси ординат. Нами показано в §6, что энергия электронов в каждой зоне является периодической функцией с периодом обратной решетки:

(5)

Для одномерного кристалла период обратной решетки равен . При этом обратная решетка является одномерной

(6)

П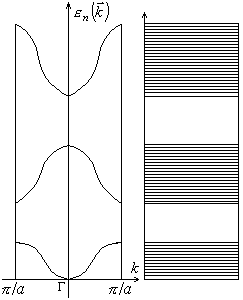 унктирными линиями на рисунке §7 отражен факт периодичности энергий в обратном пространстве решетки. В связи с периодичностью функции , соотношение (5), нет необходимости изображать все зоны Бриллюэна, а можно использовать только первую зону Бриллюэна, в которой приведены кривые , … В этом случае первая зона Бриллюэна получает название приведенной зоны Бриллюэна. Используя приведенную зону Бриллюэна можно получить всю энергетику кристалла. В этом случае энергетический спектр кристалла будет качественно выглядеть так, как показано на рисунке.

§9. Металлы, диэлектрики и полупроводники с точки зрения зонной теории твердых тел.

Н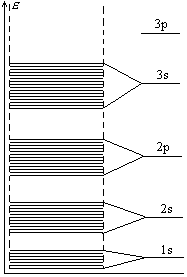 ами показано, что твердые тела имеют многозонный спектр энергии. Зонная теория твердых тел стала путеводной звездой для ученых и инженеров работающих в области твердотельной электроники, она позволяет не только объяснить удивительные свойства полупроводников но и позволяет предсказать как их можно радикально изменить. Представим себе кристалл, состоящий из N одинаковых элементов, каждый из которых содержит z электронов. Все эти электроны размещаются на энергетических уровнях соответствующих зонам кристалла. В первую очередь заполняются электронами зоны с наименьшей энергией, это электроны находящиеся непосредственно возле ядер, затем заполняются зоны с более высокими энергиями, пока не будут размещены все zN электроны. На каждом энергетическом уровне свободного (изолированного) атома могут находиться 2(2l+1) электронов: на s (l = 0) 2 электрона, на p (l = 1) 6 электронов, на d (l = 2) 10 электронов. При сближении атомов на месте одиночных уровней , , , , , образуются энергетические зоны: 1s, 2s, 2p, 3s, 3p, 3d… В каждой зоне N энергетических уровней, значит s – зоны могут вместить 2N электронов, p – зоны 6N электронов, d – зоны 10N электронов и т.д. (смотри рисунок).

В зависимости от характера заполнения электронами верхней зоны все твердые тела делятся на три группы: металлы, диэлектрики, и полупроводники. У некоторых твердых тел самая верхняя зона, содержащая электроны может быть заполнена частично, т.е. у нее имеется часть свободных уровней. Приложим к такому кристаллу внешнее электрическое поле, известно, что в конце длины свободного пробега под действием внешнего электрического поля, электроны приобретают энергию от 10^-4 до 10^-8 эВ. Эта энергия значительно больше, чем расстояние между соседними уровнями зоны (10^-22 эВ). В связи с этим электроны верхней зоны переходят на свободные уровни с более высокой энергией (смотри рисунок). При э том электрон пространственно смещается по направлению против электрического поля, что указано стрелкой. Если смещающиеся электроны непрерывно отводить от тела, что возможно в электрической замкнутой цепи, то квантовые переходы электронов, которые указаны стрелкой, будут происходить непрерывно долго, пока в цепи будет источник внешнего поля. Таким образом, твердые тела с указанным характером заполнения верхней зоны будут хорошо проводить электрический ток, такие тела являются металлами. При этом проводимость металла не возрастает с ростом температуры, наоборот, с понижением температуры электропроводность увеличивается. При комнатной температуре проводимость “хороших” металлов .

Представим себе кристаллы Na, их атомы имеют следующую электронную структуру: Na(z = 11) = 1s² 2s² 2p⁶ 3s¹. Видно, что уровень 3s содержит один валентный электрон. При образовании кристалла Na энергетические уровни , , , превращаются в зоны 1s, 2s, 2p, 3s. Последняя зона 3s будет содержать N электронов, а способна вместить 2N электронов, следовательно, последняя зона будет заполнена на половину, следовательно, кристаллы Na будут являться металлами. У некоторых кристаллов металлическая проводимость обусловлена тем, что самая верхняя зона, заполненная электронами перекрывается со следующей пустой зоной.

У многих твердых тел самая верхняя зона содержащая электроны может быть заполнена полностью электронами, а следующая за ней зона полностью пустая и отделена от предыдущей зоны большим промежутком запрещенных энергий . Такие твердые тела получили название диэлектриков (изоляторов).

В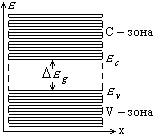 этом случае основная полностью заполненная зона называется валентной (V – зона), а следующая за ней пустая зона разрешенных энергий называется зоной проводимости (C – зона). Промежуток запрещенных энергий, который разделяет валентную зону и зону проводимости называется запрещенной зоной. Ширина этого промежутка ,где - дно зоны проводимости, - потолок валентной зоны. При T = 0 K⁰ диэлектрик не проводит электрический ток. При повышении температуры диэлектрика, электроны валентной зоны начинают взаимодействовать с колебаниями кристаллической решетки и получают от нее энергию ~ KT, но некоторые электроны получают значительно большую энергию. Процесс передачи энергии электронам – статистический. Тем неменее, число электронов, которые получают от решетки энергию ничтожно мало. Значит, будет ничтожно мало число электронов, которые способны перейти за счет тепловых переходов из валентной зоны в зону проводимости. Таким образом, твердое тело с большой шириной запрещенной зоны плохо проводит электрический ток, их проводимость примерно равна , в лучшем случае электропроводность может быть активирована высокой температурой. Исходя из зонной схемы диэлектрика, можно сказать, что валентная зона и зона проводимости не перекрываются.

Если у твердого тела при T = 0 K⁰ самая верхняя зона полностью заполнена, а следующая за ней зона проводимости пустая и отделена от предыдущей зоны не широким промежутком запрещенных энергий , то твердое тело называется полупроводником. Как видно принципиальной разницы между диэлектриком и полупроводником нет. При достаточно высоких температурах у полупроводников могут иметь место тепловые переходы из валентной зоны в зону проводимости за счет взаимодействия валентных электронов с ионами кристаллической решетки. Электроны, перешедшие из валентной зоны в зону проводимости, могут участвовать в переносе электрического тока. Появившиеся свободные уровни в валентной зоне (вакансии) будут также участвовать в переносе электрического тока. Носителями тока в валентной зоне являются дырки. Таким образом, проводимость полупроводника является активированной. При T = 0 K⁰ полупроводники как и диэлектрики не проводят электрический ток. Чем меньше , тем выше при прочих равных условиях электропроводность полупроводника. Электропроводность полупроводника лежит в широком диапазоне значений:

.