§14. Элементарная теория мелких примесных состояний полупроводника.

Как известно, мелкие примесные состояния такие, у которых энергия ионизации значительно меньше ширины запрещенной зоны .

Для определенности будем рассматривать полупроводник с мелкой донорной примесью, все выводы полученные для него будут верны для полупроводника с мелкой акцепторной примесью. Как известно орбита валентного электрона мелкого донора охватывает несколько постоянных решеток кристалла. В этом случае можно считать, что положительный ион донора взаимодействующий с валентным электроном погружен в диэлектрическую среду кристалла полупроводника. Тогда взаимодействие валентного электрона и иона можно считать по законам кулоновского взаимодействия точечных центров, следовательно, потенциальная энергия взаимодействия валентного электрона с положительным ионом будет равна:

- диэлектрическая проницаемость кристалла. Тогда полная потенциальная энергия мелкого донора будет равна:

(1)

Запишем стационарное уравнение Шредингера для валентного электрона мелкого донора:

(2)

Запишем (2) в приближении эффективной массы, влияние периодического поля кристалла учтем заменой

(3)

(3) совпадает с уравнением атома водорода, если заменить , . Значит, решение уравнения (3) такое же, как для атома H, только при соответствующих заменах.

, (4)

Из (4) следует, что энергия мелкого донора квантуется, состояние с - это основное состояние и ему соответствует энергия:

(5)

Тогда энергия ионизации в основном состоянии равна:

(6)

Из (6) следует, что энергия ионизации мелких доноров не зависит от их сорта, т.е. что энергия ионизации одинакова для любой мелкой примеси в данном кристалле. Энергия ионизации возбужденного состояния мелкого донора рвана:

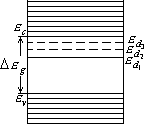, , , то .

На рисунке показана энергетическая диаграмма кристалла с донорной примесью. Для того чтобы экспериментально обнаружить состояние мелких доноров нужно использовать низкие температуры и технику миллиметрового диапазона.

§15. Зонная структура полупроводника в пространстве.

Как известно энергия электронов во всех разрешенных зонах полупроводника есть функция волнового вектора из первой зоны Бриллюэна. Зависимость называется законом дисперсии. По существу эта зависимость от длины волны . Дисперсионные кривые валентной зоны и зоны проводимости являются важнейшими характеристиками полупроводника. При этом важно знать зависимость не во всей зоне Бриллюэна, а только в небольшой ее части, вблизи абсолютных экстремумов зоны проводимости и валентной зоны, т.е. вблизи дна зоны проводимости и потолка валентной зоны.

В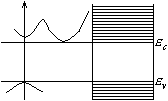 любой зоне характер зависимости вблизи точки экстремума определяется формой изоэнергетической поверхности. Эта такая поверхность, которая проведена через концы волновых векторов зоны Бриллюэна, которым соответствует заданная энергия . В любой зоне является четной функцией волнового вектора , значит, любые изоэнергетические поверхности имеют центр симметрии. Аналитическую форму изоэнергетической поверхности можно получить следующим образом. Пусть экстремум невырожденной зоны лежит в точке зоны Бриллюэна. Разложим в ряд Тейлора вблизи окрестности точки , приведя разложение к главным осям X, Y, Z. При этом

.

Ограничимся первыми тремя членами, тогда

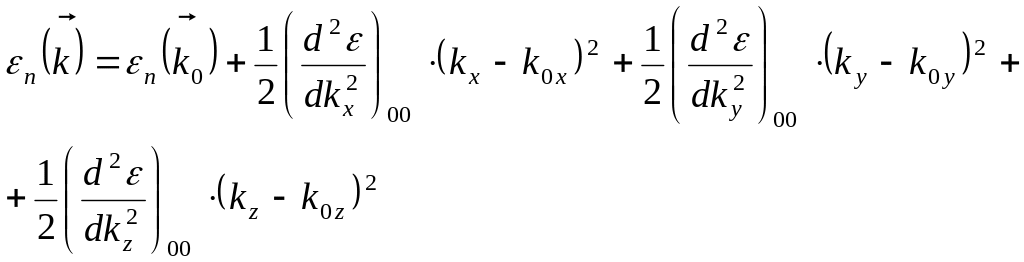(1)

(2)

- уравнение изоэнергетической поверхности. Тогда из (2) получаем уравнение изоэнергетической поверхности:

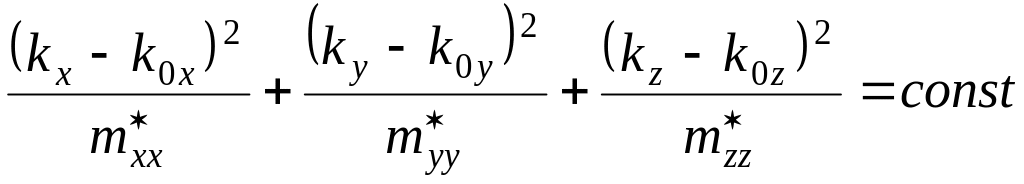(3)

(3) – уравнения эллипсоида с центром в точке .

Компоненты могут быть связанны условием симметричности изоэнергетической поверхности. Для примера рассмотрим кубические кристаллы типа A₂B₆, A₃B₅, кристаллы типа алмаза. Абсолютный минимум кристалла типа сфалерита лежит в точке , т.е. в центре зоны Бриллюэна, тогда (3) равно:

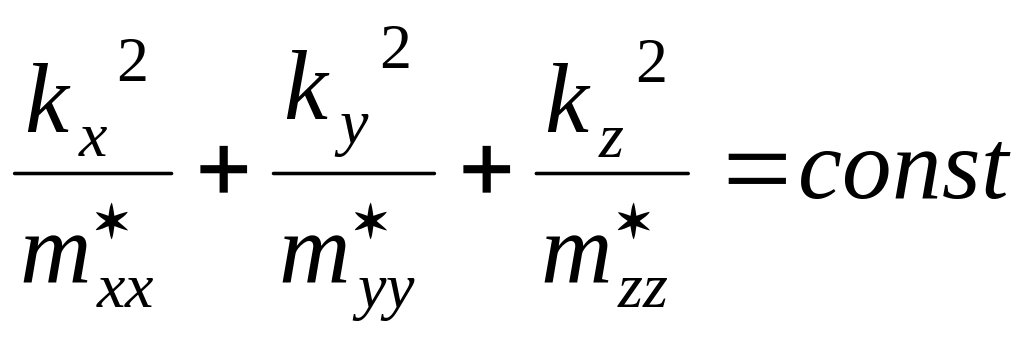(4)

С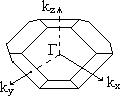 вектором связаны три оси четвертого порядка зоны Бриллюэна (усеченный октаэдр). С осями симметрии четвертого порядка связаны повороты на 90⁰, 180⁰, 270⁰, 380⁰. При этих поворотах вектор остается неизменным. Повороты вокруг этих осей совмещают кристаллическую решетку саму с собой, следовательно, и физические свойства, а также уравнения описывающие эти свойства остаются инвариантными относительно этих преобразований, т.е. уравнения описывающие изоэнергетические поверхности должны оставаться неизменными при этих преобразованиях.

Для примера совершим поворот вокруг оси на 90⁰: , (4) примет вид:

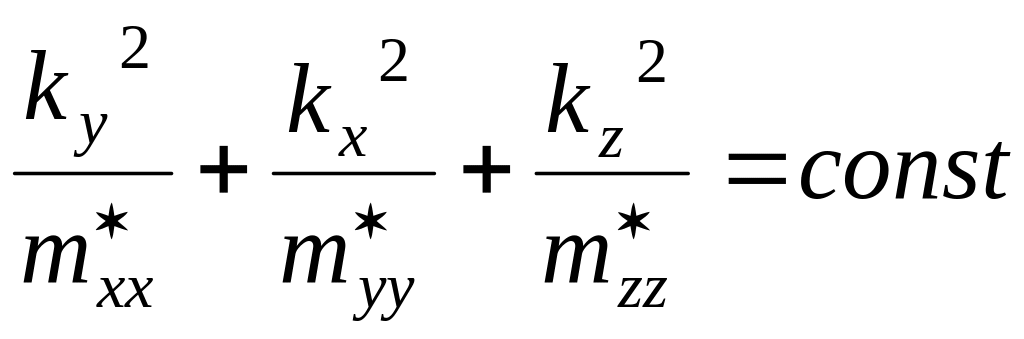(5)

Но (4) и (5) одинаковы, тогда . Совершим поворот вокруг оси на 90⁰: , следовательно, все компоненты равны: , тогда соотношение (5) примет вид:

(6)

Значит эффективная масса изотропная величина. Тогда закон дисперсии:

(7)

З акон дисперсии параболический. На сфере будут лежать волновые вектора с одинаковыми значениями модуля эффективной массы. В этом случае характеризуется четырьмя компонентами, т.е. она изотропна (эффективная масса такого экстремума сферическая).

К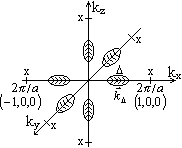 ристаллы с кубической решеткой типа алмаза: германий и кремний не прямозонные полупроводники. У них минимум зоны проводимости и максимум валентной зоны находятся в разных точках зоны Бриллюэна. Зона Бриллюэна у них тоже усеченный октаэдр. Например, у кристаллов кремния максимум валентной зоны находится в центре зоны Бриллюэна, а минимум зоны проводимости на оси , которая совпадает с осью симметрии четвертого порядка (смотри рисунок). Минимум зоны проводимости лежит на линии , на расстоянии от начала координат, т.е. модуль вектора . Вектор связан только с одной осью симметрии четвертого порядка, например на рисунке вектор связан только с осью симметрии . Произведем поворот вокруг оси и получим, что , .

В этом случае мы не имеем право вращать вокруг оси и как в предыдущем случае, потому что вектор принадлежит только одной оси, тогда уравнение (5) приобретает вид:

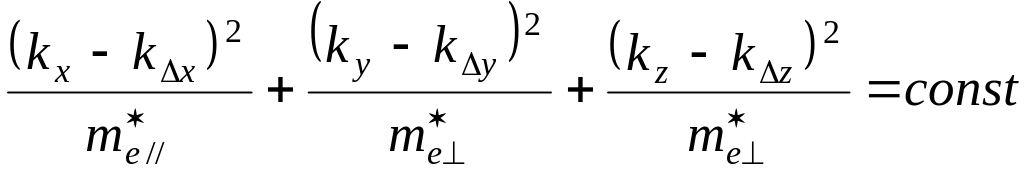(8)

В идно, что изоэнергетическая поверхность является эллипсоидом вращения с осью . - поперечная компонента эффективной массы электронов, - продольная компонента эффективной массы электронов. Значит, у кристаллов кремния абсолютный экстремум зоны проводимости характеризуется двумя компонентами эффективной массы: , .