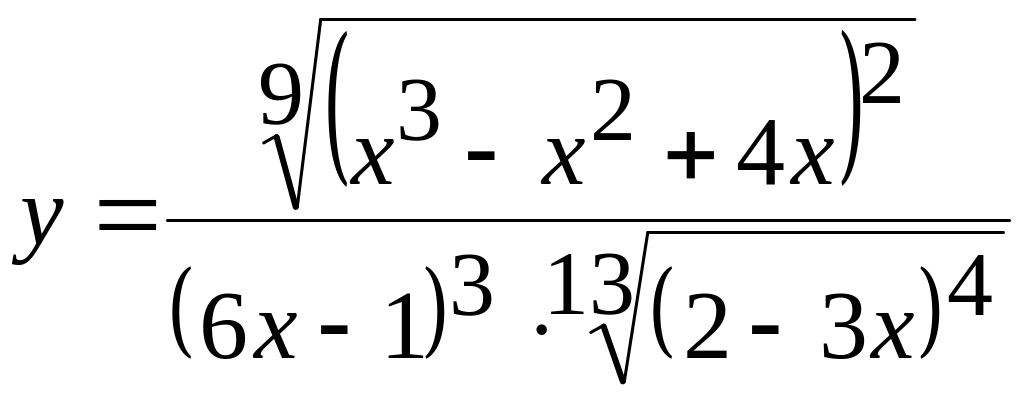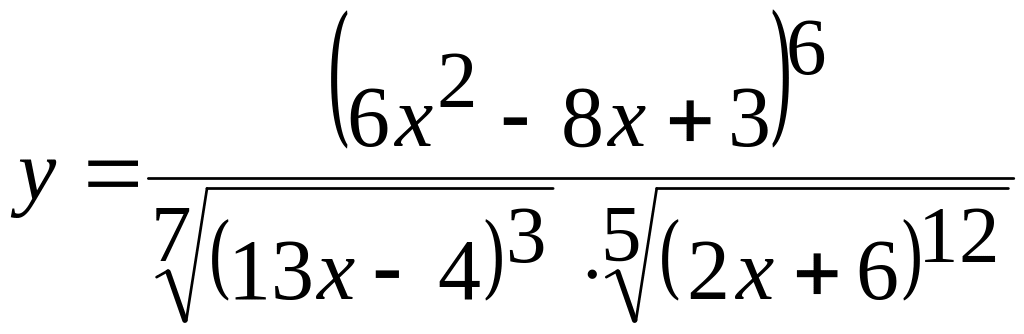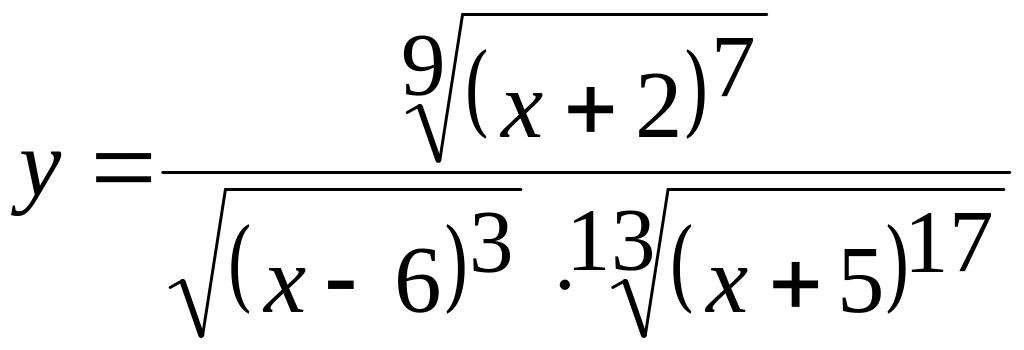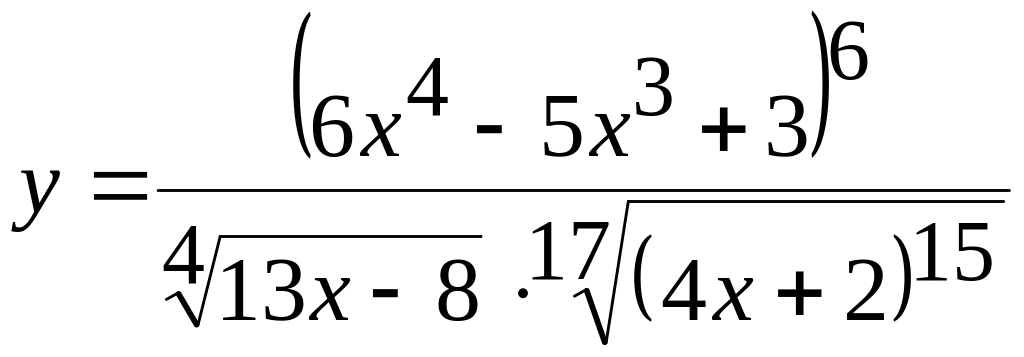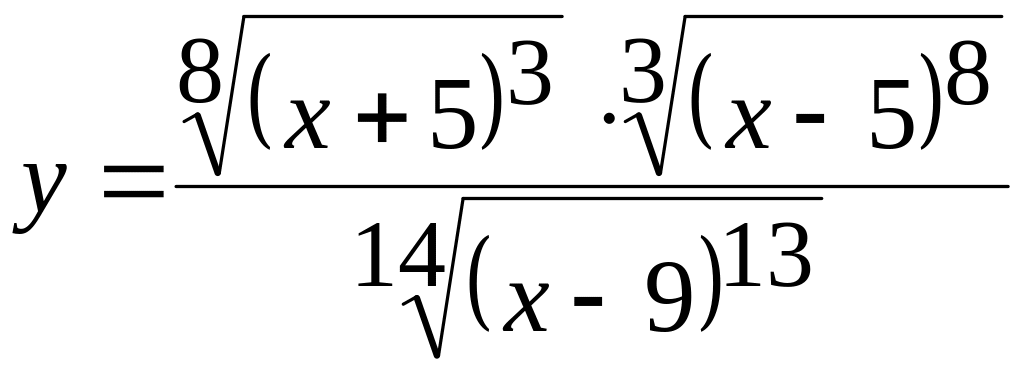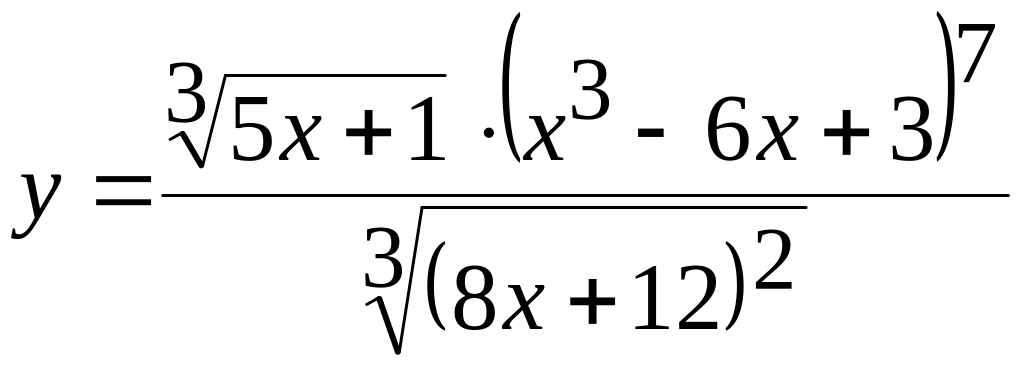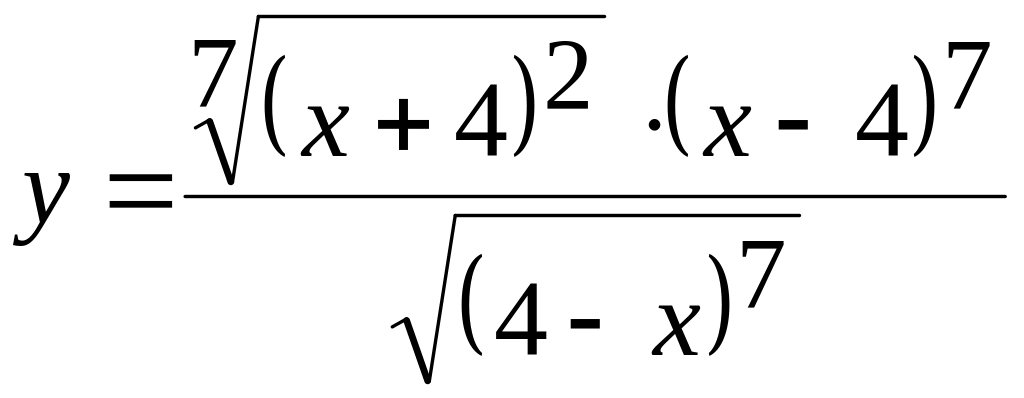1.5. Логарифмическое дифференцирование
Этот способ заключается в том, что перед тем как взять производную, функцию нужно прологарифмировать, лучше по основанию «е» (основание натурального логарифма)
Обычно применяют логарифмическое дифференцирование в двух случаях. Рассмотрим их на конкретных примерах:
Случай 1. – это функция вида:
Преобразуем функцию:
Теперь прологарифмируем:
затем, используя свойство логарифма получим:
Теперь возьмем производную:
и
выразим
Случай 2. Если функция показательно-степенная
Например:
Сначала прологарифмируем
теперь возьмем производные:
Пример:
Задание 2.
Найти производные следующих функций
Вариант 1 |
Вариант 2 |
1)
|
1)
|
2)
|
2)
|
3)
|
3)
|
4)
|
4)
|
|
|
Вариант 3 |
Вариант 4 |
1)
|
1)
|
2)
|
2)
|
3)
|
3)
|
4)
|
4)
|
|
|
Вариант 5 |
Вариант 6 |
1)
|
1)
|
2)
|
2)
|
3)
|
3)
|
4)
|
4)
|
|
|
Вариант 7 |
Вариант 8 |
1)
|
1)
|
2)
|
2)
|
3)
|
3) |
4)
|
4) |
|
|
Вариант 9 |
Вариант 10 |
1)
|
1)
|
2)
|
2)
|
3)
|
3)
|
4)
|
4)
|
|
|
Вариант 11 |
Вариант 12 |
1)
|
1)
|
2)
|
2)
|
3)
|
3)
|
4)
|
4)
|
|
|
Вариант 13 |
Вариант 14 |
1)
|
1)
|
2)
|
2)
|
3)
|
3)
|
4)
|
4)
|
|
|
Вариант 15 |
Вариант 16 |
1)
|
1)
|
2)
|
2)
|
3)
|
3)
|
4)
|
4)
|
|
|
Вариант 17 |
Вариант 18 |
1)
|
1)
|
2)
|
2)
|
3)
|
3)
|
4)
|
4)
|
|
|
Вариант 19 |
Вариант 20 |
1)
|
1)
|
2)
|
2)
|
3)
|
3)
|
4)
|
4)
|
|
|
Вариант 21 |
Вариант 22 |
1)
|
1)
|
2)
|
2)
|
3)
|
3)
|
4)
|
4)
|
|
|
Вариант 23 |
Вариант 24 |
1)
|
1)
|
2)
|
2)
|
3)
|
3)
|
4)
|
4)
|
|
|
Вариант 25 |
Вариант 26 |
1)
|
1)
|
2)
|
2)
|
3)
|
3)
|
4)
|
4)
|
|
|
Вариант 27 |
Вариант 28 |
1)
|
1)
|
2)
|
2)
|
3)
|
3)
|
4)
|
4)
|
|
|
Вариант 29 |
Вариант 30 |
1)
|
1)
|
2)
|
2)
|
3)
|
3)
|
4)
|
4)
|
