11.3.3. Защита от шума, электромагнитных полей и излучений

Уровень интенсивности в свободном волновом поле. Уравнение пло­ской волны, не затухающей с расстоянием, в комплексной форме имеет вид

(11.53)

здесь й_т = u_md^^u — комплексная амплитуда; г — радиус-вектор рас­сматриваемой точки; к — волновой вектор, численно равный волно­вому числу

к = со/с — 2 лД,

где с и X — соответственно скорость распространения и длина волны.

Распространение волны всегда связано с переносом энергии, ко­торая количественно характеризуется мгновенным вектором плотно­сти потока энергии I,. На практике обычно пользуются понятием ин­тенсивности волны /, которая равна модулю среднего значения векто­ра I, за время, равное периоду Т полного колебания. Найдем интен­сивности звука и электромагнитной волны. Для этого введем понятие импеданса среды при распространении волны.

Комплексным импедансом среды при распространении звуковой вол­ны назовем отношение

i = P/у ,

где р и v — соответственно звуковое давление и колебательная ско­рость.

Комплексным импедансом среды при распространении электромаг­нитной волны назовем отношение поперечных составляющих элек­трического (Е) и магнитного (Н) полей в данной точке:

i = E/S. (11.54)

В дальнейшем все основные соотношения, которые будут исполь­зоваться при рассмотрении звуковых и электромагнитных полей, яв­ляются однотипными. Поэтому удобно ввести следующее обозначе­ние: и = р для звука и и = Едля электромагнитного поля. С учетом это­го обозначения при определении интенсивности звуковой волны или при определении интенсивности электромагнитной волны можно использовать одну и ту же форму¹:

I=±Rz{uu/z) = u²_m/2z = uljz, ^(1L55)

где «_Эф ⁼ \^{u 2}— эффективное значение величины и.

летворяющих условию I* = ul/z*, выражение (11.55) можно записать в

При заданных стандартом референтных значениях* /*, и*, z*, удов- воряю уровнях:

Li = L_u + L_z, (11.56)

где Ц = 101g///*, L_u = 201g«_3({)/«* и L_z= lOlgz/z* — уровни величин /, и, z. Суммарная интенсивность некогерентных источников

/=1

Следовательно, уровень суммарной интенсивности

L_h = 101g/₂//,=101g£l0^0,i">

/= 1

где L_f ип — соответственно уровень интенсивности /-го источника и число источников. Если все п источников имеют одинаковый уровень интенсивности, равный Z₇, то уровень суммарной интенсивности бу­дет равен

L_h =L,+ 101g/i.

Реальные источники излучают волны неодинаково в различных направлениях. Интенсивность (/_н) и уровень интенсивности L/_H ис­точника ненаправленного действия мощностью W на расстоянии г соответственно равны:

/_н = W/An?\ L_Ih =L_w+ lOlgS^r). (П.57)

Здесь L_w= lOlg W/W* — уровень мощности при заданном рефе­рентном значении JV*, и принято условие, которое в дальнейшем всегда будет использоваться при переходе к уровням, что W* = I*S_e, где S_e — единичная площадь; = 4п?.

Источники направленного действия обычно характеризуют ха­рактеристикой (диаграммой) направленности и коэффициентом на­правленности.

Амплитудная характеристика направленности D представляет со­бой отношение колеблющейся величины и, взятой в данном направ­лении на некотором расстоянии от источника, к ее значению и*, взя­тому на том же расстоянии в направлении максимального излучения. С учетом формулы (11.55) можно записать

D = и/и*; if = I/I*. (11.58)

Коэффициент направленности определяется выражением

Ф = /Дн, (11.59)

где /— интенсивность волны на некотором расстоянии г от источни­ка направленного действия мощностью Ж, излучающего волновое поле в телесный угол Q; /_н — интенсивность волны на том же рас­стоянии при замене данного источника на источник ненаправленно­го действия той же мощности.

В общем случае в сферической системе координат характеристика направленности D и коэффициент направленности Ф зависят от уг­лов 0 и ф; D = Z>(0, ф), Ф = (0, ф). Для осесимметричных источников D = Л(в), Ф = Ф(0), т. е. они не зависят от координаты ф. Например, для многих источников характеристика направленности имеет вид:

D = £>(в) = 0,5 (т + l)cos^w0, (11.60)

где т — некоторое число.

Из определения коэффициента направленности следует

Ф- / - D¹

|IdS/Anr² JD²dS/4nr² (1Ш)

Q Q

Здесь интегрирование проводят по площади поверхности, через которую в дальнем поле излучается энергия, так как поток интенсив­ности через непроницаемую поверхность равен нулю. При характе­ристике направленности D = 1 коэффициент направленности удобно находить через значение телесного угла, в который реально происхо­дит излучение:

D² 4я _4я

\D²dS/Anr² ~ jdQ~Q ' (^1L62>

Q Q

В зависимости от местоположения источника значения коэффи­циента направленности при D = 1 соответствуют следующей таблице:

Местоположение источника излучения	Угол излучения Q	Значение коэффициента направленности Ф
В свободном пространстве	4тс	1
На плоскости	2л	2
В двугранном угле	тс	4
В трехгранном угле	тс/2	8

Таким образом, интенсивность можно выразить через мощность источника следующим образом:

| / _н Ф = ЖФ/ 4пг² -при любой характеристике направленности D;

[Ж/Ог²-при характеристике направленности D = 1. (11.63)

При необходимости учесть затухание в уравнение (11.53) вводят вместо волнового числа к комплексное волновое число к*, или коэф­фициент распространения к*\

L = y-fi = -jL, (11.64)

где у и 8 — соответственно коэффициент фазы и коэффициент зату­хания. Амплитуда затухающей волны будет равна й_т{Ъ) = й_тоГ^ъ\ а ин­тенсивность волны будет затухать по закону:

_{/(5) =} ^ ₌ ^_е-²⁵' = /е"²⁵' =/_нФе"²⁵'. ^(П'⁶⁵⁾

2z 2 z

На расстоянии г затухание интенсивности в децибелах (дБ)

е₅ = 101g///(S) = (201g e)br = 8₀r, (11.66)

где 8₀ « 8,6868 — коэффициент затухания, выраженный в децибелах на единицу длины.

Полагая W* = I*S_Q и S(r) = 4пг², из выражения (11.65) находим уро­вень интенсивности с учетом затухания:

L_m = L_lH + lOlgO - е₅ = L_w + lOlgO + lOlg(S^W) - е_ь. (11.67)

Таким образом, уровень интенсивности в данной точке определя­ется через уровень мощности и коэффициент направленности. Фор­мула (11.67) справедлива в свободном волновом поле, т. е. поле, не имеющее границ, от которых могло бы происходить отражение волн.

403

Свободное поле можно создать и в помещении, если сделать послед­нее из материала, полностью поглощающего энергию падающей вол­ны. Величину 101g<D называют показателем направленности и обозна­чают ПН.

Таблица 11.22. Коэффициент затухания звука в воздухе, дБ/км

Относительная влажность воздуха, %	Среднегеометрические частоты октавных полос, Гц
	125	250	500	1000	2000	4000	8000
10	0,8	1,5	3,8	12,1	40	109	196
40	0,4	1,3	2,8	4,9	11	34	120
80	0,2	0,9	2,7	5,5	9,7	21	66

Для звука коэффициент затухания 8₀ зависит от частоты звука, температуры, давления и относительной влажности воздуха. При нормальном атмосферном давлении и температуре воздуха, равной + 20°С, значения коэффициента 8₀ даны в табл. 11.22. Для электро­магнитной волны, распространяющейся в воздухе, 8₀« 0 (см. ниже). Следует иметь в виду, что в реальных условиях уровень затухания е_ъ зависит также от погодных условий (дождь, снег, туман и т. д.), нали­чия растительности (трава, кустарник, деревья и т. д.), состояния ат­мосферы (ветер, туман, турбулентность, температурные градиенты и т. д.), наличия отражающих поверхностей (земля, преграды, экраны

п

и т. д.) и ряда других факторов и вычисляется по формуле е_ъ =

/= 1

где вщ — уровень затухания при наличии /-го фактора. Если затуха­нием можно пренебречь (8 = 0), то уровень интенсивности

Lj= L_w+ ПН + 101g£/(4rcA (11.68)

Диффузное волновое поле в изолированных объемах. Волновое поле называют диффузным, если усредненная по времени объемная плот­ность энергии w = одинакова во всех точках, а поток энергии через единичную площадку в любой точке и в любом направлении постоя­нен и равен /д.

Для бегущей с плотностью волны интенсивность /_в = cw%, ко­торая в диффузном поле равномерно распределяется во все стороны пространства 4я и, следовательно, на полусферу приходится /_в/2. По­этому нормально к диаметральному сечению сферы радиуса г в про­тивоположных направлениях с интенсивностью /_в/2 распространя­ются две волны.

Через площадь к? этого сечения в полусферу переносится поток энергии /_вя^/2, который затем с плотностью /_д изотропно распреде­ляется по всем направлениям полусферы. Из соотношения /_вя^/2 = = /_д2я^ следует

/д = /в/4 = cwx/4. (11.69)

Таким образом, поток энергии через единичную площадку в диф­фузном волновом поле в четыре раза меньше интенсивности /_в волн, бегущих с объемной плотностью

Понятие диффузного поля часто используют при определении плотности потока энергии /_п в изолированных объемах. Под изоли­рованным объемом понимается пространство, огражденное стенка­ми (например, производственное помещение, кабина, пространство под кожухом машины и т. д.). Волны в изолированных объемах, мно­гократно отражаясь, образуют поле, которое изменяется при измене­нии геометрических размеров, формы и других характеристик источ­ника.

Волновое поле в каждой точке изолированного объема можно представить в виде совокупности волн, непосредственно приходящих в эту точку от источника — прямая волна с интенсивностью 1= cw, и совокупности волн, попадающих в нее после отражений от границ изолированного объема — отраженная волна с интенсивностью /в ⁼ cwjx (рис. 11.44). Поэтому суммарная интенсивность (/_п = cw_u) в заданной точке изолированного объема на некотором расстоянии от поверхности равна сумме интенсивностей прямой и отраженной волн:

/п = /+/в = /+4/_д. (11.70)

W/S

А

L -1 _п

а/д

L ,

н

(/= №Ф/4ю*) (h = 4W/Ip\\ £

и

В =aS/(l-a)

Рис. 11.44. Диффузное поле отраженной волны

Интенсивность прямой волны в общем случае определяется фор­мулой (11.65). Выразим плотность потока энергии /_д через мощность источника. При работе источника в изолированный объем постоянно поступает энергия. При мощности источника Ж отраженный от гра­ниц полный поток энергии составит plV, а от единичной площад­ки — р W/S. За единицу времени через единичную площадку границы вследствие поглощения исчезнет количество энергии, равное а/_д. Так как в диффузном поле плотность энергии постоянная, то должно соблюдаться равенство р W/S = а/_д. Для простоты дальнейших рассу­ждений здесь предполагается, что коэффициент а значительно боль­ше коэффициента т. Уравнение (11.70) принимает вид

4 nr a S

Из полученного выражения видно, что в изолированном объеме плотность потока энергии получает некоторое приращение, которое аналитически обусловлено наличием множителя (1 - a)/a, который велик при коэффициенте а, близком к нулю.

В изолированных объемах малых размеров затуханием звука с рас­стоянием можно пренебречь, полагая в формуле (11.71) 8 = 0.

Защитные устройства бесконечной и конечной толщины

Теоретическое защитное устройство бесконечной толщины мож­но рассматривать просто как среду, бесконечно простирающуюся в направлении распространения волны. Волна из одной среды прохо­дит в другую (защитное устройство), предварительно попадая на гра­ницу раздела этих сред, при этом в общем случае существуют три вол­ны: падающая, отраженная и преломленная (прошедшая).

При прохождении границы раздела сред без поглощения должен соблюдаться закон сохранения энергии, который можно записать в виде Г + Г = /⁺, и для рассматриваемых величин п (звукового дав­ления и напряженности электрического поля) равенство амплитуд поля в среде / и среде j : и_т + и~_т = и_т) (рис. 11.45). Эти соотношения совместно с формулой (11.55) позволяют найти амплитудный коэффи­циент отражения Ry и амплитудный коэффициент передачи Ту при нормальном падении волны на границу (/, у) из среды /:

Zj-Z_t , 2_ZJ (11.72)

^Kij= > ^Iij= •

z j zj у zj

("J²

AX

V

Среда i Zi

r=(u~)²/Zj

^Cpe;^ay _u~ JJ r=₍

и

Среда 1 Z]

R-u~/u+

Среда 2 Z₂

Т= и~/и⁺

^ и~

Z3 Среда 3

Рис. 11.45. Баланс энергии на границе раздела сред

Рис. 11.46. Схема защитного устройства конечной толщины

При этом имеем Т_&= 1 + R₉,R₉ = - R_&,- 1 < Д/< 1,0< Т_у<2.

В общем случае защитное устройство имеет конечную толщину. Для случая, когда гармоническая волна из среды 1 (рис. 11.46) падает на защитное устройство произвольной толщины h, состоящее из сре­ды 2, ограниченной с другой стороны средой J, амплитудные коэф­фициенты отражения и передачи равны [2].

, q + ga^+fca-Pe-". (П-73)

(1 + £₃₂)е -1)е

Т= 4W[(1 + - (Zn ~ 1)е-"]. 01.74)

Здесь коэффициент отражения записан аналогично формуле (11.72) через входной импеданс защитного устройства — £_вх, zn ^{= =} i\/Z2, Z32 = Z3/Z2, где Zu z₂, Z3 — импедансы сред (в общем случае ком­плексные величины).

Если по обе стороны от защитного устройства находится одна и та же среда, то импедансы сред i\ и равны. Тогда формулы (11.73) и (11.74) преобразуются к виду

R = {_Z~1 +*₁₂)/иГ2 +z₁₂)+2cth£.A; (11.75)

Т = [chit. А +0,5 (Zn + z₁₂ )shik]-¹.

Эти амплитудные коэффициенты R и Г при нормальном падении волн связаны с энергетическими коэффициентами р и т соотноше­ниями р = jR², т= Т\ эффективность защиты

е = 20lg|{chit.A +0,5(^2 +z_n)shLh]\. (11.76)

(11.77)

407

е = е_к + e_z+ е_И,

В некоторых случаях для расчета эффективности защиты удобно вместо выражения (11.76) использовать следующую запись:

где ^ = (201ge)8A, e_z = 201g | 0,25(1 + z_nf/z_n e_h = 201g | [1 - (1 - - z₁₂)²e~²^/( 1 + Zi₂)²] I — слагаемые эффективности за счет ослабле­ния волн соответственно в материале защитного устройства, при про­хождении границы раздела сред (1,2) и при многократных отражени­ях внутри защитного устройства. Так как с увеличением частоты ко­эффициент к* возрастает, то e_h -> 0 и эффективность изоляции высо­кочастотных полей е&е_к + e_z.

Прогнозирование шума. Условие безопасности при наличии звуко­вого поля можно записать в виде неравенства

L_p(J)<L_mu(J), (11.78)

где L_p(f) = 201g\р_эф(/)/р* и L_mu(f) — соответственно уровни звукового давления и их нормативные значения. Неравенство (11.78) должно выполняться на всех среднегеометрических частотах и во всех точках рассматриваемого пространства с учетом времени звукового воздей­ствия. Из соотношения (11.56) следует

L_p = Lj-L_z. (11.79)

Референтные значения звукового давления, интенсивности и им­педанса равны: р* = 2 • Ю^-5 Па, I* = 10~¹² Вт/м², z* = 400 Па • с/м.

Характеристический импеданс среды для звука равен произведе­нию скорости звука в среде с на ее плотность р: z = рс. Для атмосфер­ного воздуха при р = 1,29 кг/м³ и с = 331 м/с, z = 430 кг/(м² • с).

Таблица 11.23. Плотность, скорость звука и характеристический импеданс для некоторых сред и материалов

Среда, материал	Плотность р, кг/м3	Скорость звука с, м/с	Импеданс z — рс, Па • с/м
Водород	0,084	1310	110
Вода	1000	1450	1,45 • 106
Бензин	750	1190	0,89 • 106
Алюминий	2650	6220	16,5 • 106
Медь	8930	4620	41,3 • 106
Сталь	6110	7800	47,7 • 106
Стекло	2500	4900... 5900	(12...15). 106
Полистирол	1160	2670	3,1 • 106
Железобетон	2400	4500	11 • 106
Кирпич	1500	2750	4,1 • 106
Пробка	240	500	0,12- 106
Резина (техническая)	1200	60	0,72 • 106

Значение импеданса зависит от температуры и давления. Однако при изменении давления и температуры в пределах обычной атмо­сферы уровень импеданса L_z = 10 lgz/z* незначителен и им пренебре­гают, полагая, что

Ш) = W).

В табл. 11.23 приведены значения импеданса z для разных сред. Уровень интенсивности звука в свободном волновом поле можно определить, используя зависимости (11.67), (11.68).

При определении уровня интенсивности в изолированном объе­ме в общем случае необходимо учитывать наличие диффузного вол­нового поля, которое зависит от значений коэффициента звукопо­глощения а. Значения коэффициента а вычисляют по правилу: для частот / = 63... 1000 Гц и принимают а = а₀, где а₀ определяют по табл. 11.24; для частот /= 2000...8000 Гц коэффициент а вычисляют

по формуле а = 1 - (1 — а₀)ехр(— 287), где 8 в нужной размерности (см. формулу (11.66)) находят с помощью табл. 11.22, а постоян-

п

ная затухания звуковой энергии в объеме К равна / =4V при

/=1

п

этом = S — площади ограждающих изолированных объемов

/=i

поверхностей. Некоторые ориентировочные значения коэффициен­та звукопоглощения даны в табл. 11.24. Если стенки изолированного объема изготовлены из п разных материалов, то среднее значение коэф­фициента звукопоглощения

a =W_a/W =

2Х

(11.80)

Зная среднее значение коэффициента звукопоглощения, можно определить постоянную изолированного объема, имеющую размер­ность площади:

г* Z^a/⁵/

a S

В =

(11.81)

l-a 1 -S_a/S 1-£аЛ/2>,'

Пренебрегая затуханием звука с расстоянием, запишем выраже­ние (11.70) в виде

/п = /+ /_в = /н(Ф + Ф') = — (Ф + Ф') . ^(1L82)

S(r)

Здесь для точек г на некотором удалении от ограждающих поверх­ностей коэффициент влияния диффузного поля

ф' = /в//н = 4/д//н = Щг)/В, (11.83)

где S(r) = 4пг². Влияние диффузного поля тем сильнее, чем больше расстояние г от источника звука и чем меньше коэффициент звуко­поглощения а. Точки пространства, в которых Ф = Ф', лежат на ус­ловной границе между зоной прямого звука и зоной отраженного звука. Они расположены от источника на расстоянии

г. = ^ВФ/16п.

Разделив левую и правую части выражения (11.82) на референтное значение 7*, найдем уровень интенсивности в точке г:

L_In = L_lH + 10 lg(0 + Ф'), (11.84)

где уровень интенсивности источника ненаправленного действия Lj определен формулой (11.57).

При больших значениях коэффициента поглощения а значение постоянной В -> оо и, как следует из формулы (11.83), во всех конеч­ных точках изолированного объема коэффициент Ф' = 0. Выражение (11.84) не будет отличаться от формулы (11.68) расчета уровня интен­сивности в свободном звуковом поле. Все пространство изолирован­ного объема заполнено прямым звуком. На практике, если Ф/Ф' < 0,26 или Ф'/Ф < 0,26, то с точностью до 1 дБ в выражении (11.84) можно полагать, что 10 lg(® + Ф') соответственно равно 10 lgO^f или 10 IgO.

Заметим, что радиус г проводят из точки, в которой расположен источник, а для реальных источников — из акустического центра, при этом если источник расположен на плоскости, то акустический центр совпадает с проекцией геометрического центра источника на эту плоскость.

Интенсивности отраженных и прямых волн начинают определен­ным образом складываться на некотором удалении от ограждающих поверхностей, на которые падает поток энергии с интенсивностью

/п = /+/д = /_н(Ф + Ф'), (П.85)

где значение коэффициента влияния диффузного поля в точке R на ограждающей поверхности равно Ф' = S(R)/B.

Таблица 11.24. Коэффициент поглощения а в производственных помещениях

Тип помещения	С		реднегеометрическая частота f, Гц
	63	125	250	500	1000	2000	4000	8000
Машинные залы, ис­	0,07	0,08	0,08	0,08	0,08	0,08	0,09	0,09
пытательные стенды
Механические и ме­таллообрабатывающие цехи; цехи агрегатной	0,10	0,10	0,10	0,11	0,12	0,12	0,12	0,12
сборки в авиа- и судо­
строительной промыш­
ленности
Цехи деревообработ­	0,11	0,11	0,12	0,13	0,14	0,14	0,14	0,14
ки, посты управления, лаборатории, конструк­торские бюро

Звукопоглощение. Для уменьшения отраженного звука применя­ют защитные устройства, обладающие большими значениями коэф­фициента поглощения, к ним относятся, например, пористые и резо­нансные поглотители.

Звуковые волны, падающие на пористый материал, приводят воз­дух в порах и скелет материала в колебательные движения, при кото­рых возникает вязкое трение и переход звуковой энергии в теплоту.

Будем определять коэффициент отражения защитных устройств по формуле (11.72), аналогичной защитному устройству бесконечной толщины. Для защитного устройства бесконечной толщины коэффи­циент передачи т равен нулю и, следовательно, а = 1 — р. Так как при нормальном падении звуковых волн на поверхность защитного уст­ройства энергетический и амплитудный коэффициенты отражения связаны зависимостью р = i?², то

Р = [(*„ -z_x)/(z_BX +Z,)]²; а = 1 -р, (11.86)

где Z\ — импеданс воздуха. Входной импеданс определяется по фор­муле (11.73). Для пористого поглотителя, находящегося на акустиче­ски жесткой стенке, импеданс z₃ = °° и, следовательно,

z_BX = z₂cihk*h .

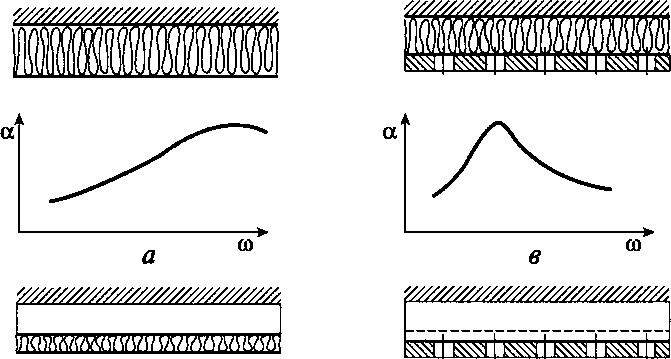
Этому случаю соответствует частотная характеристика коэффи­циента а, показанная на рис. 11.47, а. Для усиления звукопоглощения на низких частотах между пористым слоем и стенкой делают воздуш-

- со со

б г

Рис. 11.47. Частотные характеристики коэффициента поглощения:

а — для пористого поглотителя на жесткой стенке; б — для пористого поглотителя с воздушной прослойкой; в — при наличии перфорированного экрана; г — для резонансного поглотителя, об­разованного перфорированным экраном

ную прослойку (см. рис. 11.47, б). Входной импеданс защитного уст­ройства, расположенного на «мягком» основании (z₃ ⁼ 0), равен

£_вх =z₂thLh.

Пористые поглотители изготовляют из органических и минераль­ных волокон (древесной массы, кокса, шерсти), из стекловолокна, а также из пенопласта с открытыми порами. Для защиты материала от механических повреждений и высыпаний используют ткани, сетки, пленки, а также перфорированные экраны. Последние существенно изменяют характер поглощения звука защитным устройством (см. рис. 11.47, в).

Резонансные поглотители имеют воздушную полость, соединен­ную отверстием с окружающей средой. Воздух в резонаторе выполня­ет роль механической колебательной системы, состоящей из элемен­тов массы, упругости и демпфирования. Если пренебречь рассеива­нием звуковой энергии, то импеданс резонатора г_ъ равный механиче­скому импедансу (см. формулу (11.48)), отнесенному к единице площади, будет равен нулю на частоте со = со₀ ^s <JG / М . При импе­дансе резонатора Zi ⁼ 0 коэффициент отражения звукового давления 412

R = — 1. Таким образом, снижение шума происходит за счет взаимно­го погашения падающих и отраженных волн.

Резонансным поглотителем является также перфорированный экран с отверстиями, затянутыми тканью или мелкой сеткой (см. рис. 11.47, г), который существенно меняет характер поглощения. Порис­тые и резонансные поглотители крепят к стенкам изолированных объемов.

Кроме того, звукопоглощение может производиться путем внесе­ния в изолированные объемы штучных звукопоглотителей, изготов­ленных, например, в виде куба, которые в производственных поме­щениях чаще всего подвешивают к потолку.

К хорошим звукопоглощающим материалам относят те, которые на среднегеометрических частотах октавных полос 250, 500, 1000, 2000 Гц имеют коэффициент а, равный или превышающий соответ­ственно значения: 0,2; 0,3; 0,4; 0,5.

Обозначив параметры после установки поглощающих материа­лов значком ^А над буквой, запишем новое значение интенсивности звука в виде

/_п =/_н(Ф+ФГ (11.87)

Так как постоянная изолированного объема В > В, то в произ­вольной точке г изолированношобъема коэффициент Ф' < Ф' и новое значение интенсивности звука /_п будет меньше значения /_п. Разде­лив соответственно левые и правые части друг на друга, найдем

ф+Ф'

(11.88)

h

_Ф+Ф'_

Ф+Ф' Ф+Ф'

Следовательно, эффективность звукопоглощения

(11.89)

_? = £_/n-£_?n=101g

Так как при коэффициенте а -> 1 коэффициент Ф' 0, то макси­мальная эффективность, которую можно достичь звукопоглощени­ем, равна

^ах=101_ё(1+Ф'/Ф). (11.90)

В это выражение не входит ни один показатель изолированного объема, который характеризовал бы его новые звукопоглощающие свойства. Максимальная эффективность определяется значением па­раметров изолированного объема до его акустической обработки.

Из принципа непрерывности звукового давления следует, что ин­тенсивность не может претерпевать разрывов и, следовательно, ко­эффициент Ф' должен изменяться монотонно на отрезке 0 < г < R или О < г/R < 1, где R — расстояние от источника до произвольной точки на ограждающей поверхности, т. е. Ф' = Ф'(r/R).

В точке г = R на ограждающей поверхности Ф'(1) = S(R)/B. Учи­тывая соотношение (11.83), можно из точки (1, Ф' (1)) провести пара­болу, сопряженную с параболой Ф'(r/R) = 4(г/7?)²Ф'(1), и представить коэффициент влияния диффузного поля выражением

_ф(г/к)=Ыг/Р)²Ф'(1),если0<г/Р<0,25 (11.91)

^Г \[\-Mr/R-\)²/ 3]Ф'(1), если 0,25 <r/R< 1.

Рассмотрим пример. Для простоты допустим, что изолированный объем имеет форму сферы, источник расположен в центре сферы: Ф = 1, коэффициент звукопоглощения до проведения акустической обработки равен а = 0,07.

Используя соотношение (11.81), находим, что на поверхности, ог­раждающей изолированный объем, Ф'(1) = S(R)/B = (1 — а)/а. Фор­мула (11.90) показывает, что при заданном значении а = 0,07 приме­нением звукопоглощающих материалов можно добиться максималь­но возможного снижения уровня интенсивности звука на е_тах = = 101gl/a* 11,55 дБ.

Реальное значение эффективности звукопоглощения будет мень­ше 11,55 дБ. Например, при a =0,9 по формуле (11.89) находим е = 11,09 дБ. Если формулу (11.89) представить в виде двух слагаемых: е = 10 lg В/В + 101g[(l + Ф/Ф')/0 + Ф/Ф')], то получим в = = 20,78 — 9,69 = 11,09 дБ, т. е. величиной второго слагаемого пренеб­регать нельзя.

Используя выражение (11.91), найдем, что в точках r/R = 0,1; 0,2; 0,4; 0,6; 0,8 значения е_тах соответственно равны 1,85; 4,95; 8,98; 10,59; 11,32, и при a = 0,9 реальные значения е будут отличаться незначи­тельно: 1,83; 4,88; 8,74; 10,24; 10,91.

Звукоизоляция. Звукоизоляция — уменьшение уровня шума с по­мощью защитного устройства, которое устанавливается между источ­ником и приемником и имеет большую отражающую и (или) погло­щающую способность. Обычно роль защитных устройств выполняют глушители шума, экраны или стенки изолированных объемов. На­пример, защитным устройством является кожух, которым закрывают машины и механизмы, или кабина, в которой находится оператор, управляющий рабочим процессом. Стенки кожухов и кабин изготов- ляют из листового проката и покрывают изнутри звукопоглощающим материалом. Эффективность звукоизоляции с помощью стенки тол­щиной h можно определить по формуле (11.76). Если пренебречь за­туханием звука в материале, т. е. положить в формуле (11.76) коэффи­циент распространения к*, равным jk₂, где к₂ = со/с₂ — волновое чис­ло, то эффективность

в = 101g[cos²£₂/* + 0,25(^i + zi/z₂)²sm²k₂hl (11.92)

где Z\ ⁼ Р\С_Х — импеданс воздуха; z₂ — р₂с₂ — импеданс материала за­щитного устройства.

Из выражения (11.92) следует, что эффективность звукоизоляции равна нулю при толщине стенки h = пк₂/1, т. е. кратной половине длины волны (п = 0, 1,2, ...), а максимальная эффективность будет иметь место, если толщина стенки h = (2п + 1)А,₂/4.

Так как для защитного устройства, находящегося в воздухе, всегда выполняется неравенство pi с <<р ₂с₂, то для тонкой стенки (h₂«X₂/2n) из выражения (11.92) находим

е= 101g[l + (mco/2piCi)²], (11.93)

где т = p₂h — поверхностная плотность (масса защитного устройст­ва, отнесенная к единице площади).

При достаточно больших частотах единицей в правой части фор­мулы (11.93) можно пренебречь:

е = 20 lg = 20 lg (mf) -const. ⁽¹¹ *⁹⁴⁾

2_Plc,

Как видно из формулы (11.94), единственным свойством защит­ного устройства, определяющим эффективность звукоизоляции при принятых допущениях, является поверхностная плотность т. Эф­фективность звукоизоляции растет с увеличением плотности т и час­тоты / Константу, входящую в выражение (11.94), определяют, осред- няя коэффициент передачи т по углам падения. Если т и/выражены соответственно в кг/м² и Гц, то константа равна 47,5 дБ.

Найдем требуемую эффективность звукоизоляции. По определе­нию

в = lOlgl/x = lOlgJKVW~ = Z_w+ - L_w~ (11.95)

Перепишем это выражение в виде

JV~=JV⁺10-°>¹\ (11.96)

где И^/Г+, W ~ — соответственно падающий на поверхность площадью S⁺ и прошедший через эту поверхность поток энергии. Если эффек­тивность звукоизоляции рассчитывается по формуле (11.94), то 10~°'^1е = (2р₁с₁/тсо)². Плотность потока энергии, падающего на ограж­дающие стенки и другие поверхности, находящиеся в изолированном объеме, в точке R рассматриваемой поверхности равна

/⁺ = /+/_д = /_нФ + /_д, (11.97)

где /_н = W/Anf? — интенсивность источника ненаправленного дей­ствия.

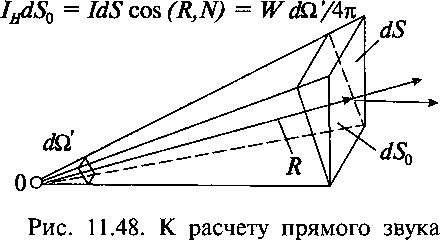
Определим сначала вклад прямого звука в поток W*. Пусть под малым телесным углом dQ! из точки О, в которой расположен источ­ник, видны элемент сферической поверхности площадью dS₀ и эле­мент несферической поверхности площадью dS⁺, которые ввиду их малости можно считать плоскими с углом между ними, равным (N, R), где N-нормаль к площадке dS⁺ (рис. 11.48). На элементарные пло­щадки dS₀ и dS⁺ падает одинаковый поток энергии, равный I_Hd$o = 7hCos(N, R)dS⁺. При характеристике направленности излуче­ния D = 1 вклад прямого звука составит

fo/_Hcos(N,R)^=^ = (Н.98)

/ ^н 4я / R² 4п а

где Q' — телесный угол, под которым из точки О видна поверхность площадью S⁺, на которую падает прямой звук; Q — телесный угол, в который источник мощностью W излучает звук.

Определим теперь вклад отраженного звука. Согласно определе­нию диффузного поля, плотность потока энергии /_д одинакова во всех направлениях. Поэтому вклад отраженного звука в поток W⁺ со­ставит

jl^dS⁺= WS⁺/B. (11.99)

s*

Таким образом, при мощности источника излучения Wсуммар­ный поток энергии, падающий на поверхность площадью S⁺, находя­щуюся в изолированном объеме, равен

W* = ЩП'/П + S⁺/B). (11.100)

Выражение (11.96) позволяет определить прошедший через эле­мент поверхности поток энергии и его уровень:

W~ = ЩП'/П + S⁺/B)l0~°'^le; (11.101)

L_w~ =L_W+ 10 lg(Q'/Q + S⁺/B) - e. (11.102)

Если шум излучается через элемент поверхности, который может рассматриваться как новый точечный источник мощностью W~> то, подставив значение в формулу (11.57) вместо W, находят уровень интенсивности источника ненаправленного действия 7/_н, что позво­ляет использовать все ранее полученные соотношения. Требуемую эффективность звукоизоляции определяют из условия (11.78).

Допустим, что шум излучается из изолированного объема в сво­бодное пространство, например на территорию жилой застройки. Считая, что элемент поверхности площадью S⁺ является новым ис­точником шума с коэффициентом направленности Ф, из соотноше­ний (11.67) и (11.102) находим, что в точке гжилой застройки уровень интенсивности

L_m =L_W+ 10 lg(Q'/Q + S⁺/B) + 10 lg® + (11.103) + 10 \gS_e/4nr - е-е_ъ,

где эффективность звукоизоляции е может быть вычислена по фор­муле (11.94). Если ставится задача определить для точки г требуемую эффективность звукоизоляции, то из неравенства (11.78) и соотно­шения (11.103) находят ее значение

e>L_w- L_mn + 10 lg(Q'/Q + S⁺/B) + 10 lg® + (11.104) + 10 \gSJ4nf- £5

Допустим теперь, что шум излучается из одного изолированного объема в другой через элемент поверхности площадью S⁺. Будем обо­значать параметры, относящиеся к изолированному объему, в кото­ром расположен источник шума мощностью W, индексом 7, а пара­метры, относящиеся к изолированному объему, где расположен при­емник,— индексом 2.

417

14-Белов

Для точечного источника шума, находящегося в изолированном объеме 7, образованном стенками кожуха (рис. 11.49, а) и излучаемо­го шум в изолированный объем 2 (например, помещение), имеем

Q = Q' = 4я и S⁺ = S. По формуле (11.101) определяем прошедший через поверхность S⁺ поток энергии: W~ = W\QT^0,le/a\. Рассматривая эту поверхность в качестве источника шума, находим, что интенсив­ность звука в точке г помещения 2 равна

Переход к уровням с учетом неравенства (11.78) позволяет запи­сать

L_Im = L_w- 10 lgoii + 10 lg(<P₂ + Ф'₂) + 10 lgS_e/S₂(r) - e < L_mn.

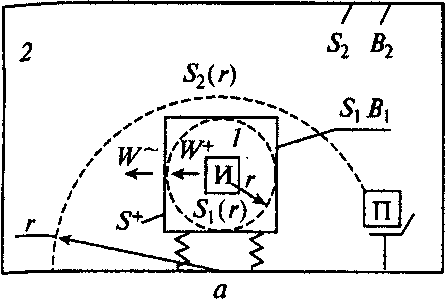
На рис. 11.49, б показано помещение 7, из которого в помещение 2 может проникать шум, при этом через элемент поверхности площа­дью S⁺ поступает поток энергии, который определяется формулой (11.101). Рассматривая эту поверхность как источник шума в помеще­нии 2 и используя формулы (11.101) и (11.102), находим требуемое ус­ловие для уровня интенсивности звука:

L_Im = L_w+ 10 lg(Q'/Q + S⁺/B_{) + + 10 1_ё(Ф₂ + Ф'₂) + 10 lgS_e/S₂(r) - e < 1_доп,

где при данном расположении источника Q = 2я, Q' — телесный угол, под которым из акустического центра источника шума виден элемент площадью S⁺.

На рис. 11.49, в показана кабина, защищающая оператора от шума, создаваемого источником в помещении I. Будем считать, что для точек г кабины, удаленных от ограждающей поверхности, вклад прямого и отраженного звука приблизительно один и тот же.

Тогда Ф₂ = Ф₂ = 4S₂(r)/B₂. Следовательно,

Ц_т = W + Ю lg(Q'/Q + S⁺/B_{) + 10 lg8S_e/B₂ - e < 1_доп,

где S⁺ и Q' — соответственно площадь поверхности кабины, через которую может проникать отраженный звук и телесный угол, под ко­торым видна поверхность кабины, на которую падает прямой звук от источника.

При установке экрана между источником и приемником (рис. 11.50) за экраном образуется звуковая тень. Уровень шума в теневой зоне от точечного источника может быть рассчитан на основе законов дифракции. Эффективность звукоизоляции при защите экраном

е = 20 lg(V2^V7th y/2nN) + 5,

| D 1 V 1 В\ 1 ' ! 1			j hW ' 1
			2
И1	S+

Рис. 11.49. Схемы снижения шума:

а — изолирующим кожухом; б — звукоизо­лирующей перегородкой; в — с помощью звукоизолирующей кабины

	"7
1 г>г*			уВ2		2 W~
X		ч \ \		П	/
/ \	*	\		Т	/

где N— число Френеля; N= ±2(а + b - d)/X (формула применима при условии N> - 0,2). Кроме того, формулу не рекомендуется при­менять при малых теневых углах 0. Если не выполняется указанное неравенство, то е = 0. Расстояние (а + Ь) складывается из расстояния а от источника до верхней кромки экрана и расстояния от верхней кромки экрана до приемника. Число Доберется со знаком минус, если экран расположен ниже визирной линии (расстояние по визирной линии между источником и приемником равно d). Экраны, установ­ленные в производственных помещениях, обычно покрывают с од­ной или двух сторон поглощающим материалом.

Рис. 11.50. Схема снижения шума экра­ном

шшшшш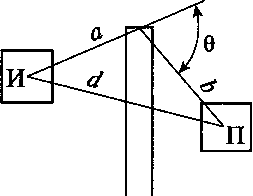

Кожухи и кабины, рассмотренные выше, имеют технологические отверстия (например, отверстия или проходы для воздуха в целях вен­тиляции), через которые может проникнуть шум. Во время рабочего цикла ряда установок (компрессоров, двигателей внутреннего сгора­ния, турбин и др.) через специальные отверстия происходит истечение отработавших газов в ат­мосферу и (или) всасывание воздуха из атмосфе­ры, при этом генерируется сильный шум. В этих случаях для снижения шума используют глуши­тели.

Система глушения шума включает источник шума, обладающий некоторым внутренним им-

14*

419

мтщтщ

W _di W+dW

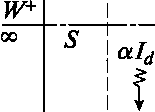
шшшшшш

ЦТ

00

A

В

I

a

б

Рис. 11.51. Применение в глушителе поглощающих материалов:

а — схема активного элемента глушителя; б — схема снижения шума при повороте трубо­провода, покрытого изнутри звукопоглощающим материалом

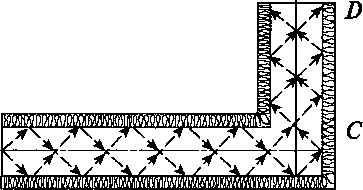
педансом источник соединен с помощью трубопровода длиной 1_Х с глушителем шума, а трубопроводом длиной /₂ — с приемником шума, который характеризуется импедансом излучения z_n- Эффективность глушения определяют по формуле (11.95), полагая, что W* — усред­ненная во времени звуковая мощность на входе в глушитель, а W~ — на выходе. Конструктивно глушители состоят из активных и реактивных шумоглушащих элементов. Простейшим активным эле­ментом является любой канал, стенки которого покрыты изнутри звукопоглощающим материалом.

Если звуковая мощность в сечении площадью S(рис. 11.51, а) рав­на Ж, то плотность потока энергии, падающего на поверхность стен­ки канала, по формуле (11.69) равна /_д = W/4S. Таким образом, на по­верхности канала площадью Pdl (где Р — периметр) поглощается зву­ковая мощность dJV= — а/_дРс1/и эффективность активного элемента

1,09а PI/S.

Трубопроводы всегда имеют повороты, которые будут снижать шум, если их покрыть звукопоглощающим материалом. Как видно из рис. 11.51, б, на участке АВ существуют преимущественно волны, на­правленные вдоль оси канала (другие волны будут поглощаться). Из­гиб канала будет поглощать или отражать осевые волны назад к ис­точнику. Таким образом, после изгиба останутся преимущественно дифрагированные волны, которые в значительной мере подавляются на участке CD, так что в конце этого участка останутся ослабленные волны в направлении оси канала.

30 25 20 15 10

5

0 0,4 0,8 1,2 1,6 2,0 2,4 2,8 п kl=2nl/X б

Рис. 11.52. Реактивный камерный элемент глушителя:

а — схема элемента; б — зависимость эффективности камерного глушителя от длины каме­ры и отношения площадей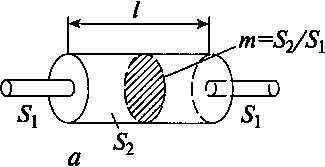

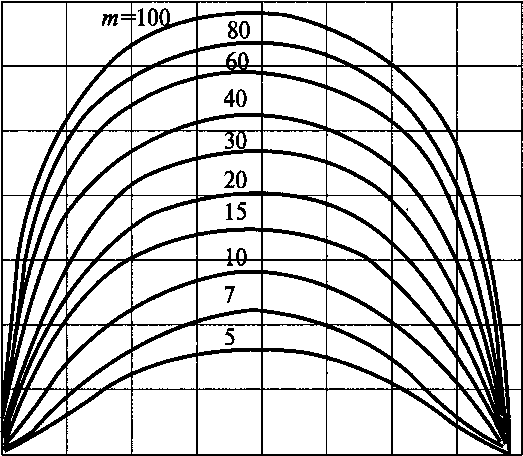
Реактивный камерный элемент (рис. 11.52) представляет собо# участок канала (трубы), на котором внезапно меняется площадь сече- ния от Si до S₂ и образуется камера длиной /. При изменении площади сечения звук отражается. Эффективность камерного элемента можно определить по формуле (11.92), заменив отношение импедансов на отношение площадей [см. формулу (11.76)] и толщину h на длину / ка­меры (к₂ = к = со/с):

с = 101g[cos²&/ + 0,25(^/^2 + S₂/S_l)²smkl\.

На очень низких частотах, когда kl^> 0 или когда длина глушите­ля равна Х/2, X, ЗХ/2 и т. д., образуются стоячие волны, которые уве­личивают давление на концах камерной полости. В результате импе­данс трубопровода с поперечным сечением S₂ также увеличивается от значения рc/S₂ до значения mpc/S₂, которое в точности равно импе- дансам входного и выходного трубопроводов, т. е. равно рс/S\. Таким образом, на этих резонансных частотах взаимодействие волн приво­дит к рассогласованию импедансов и отражению звуковой энергии к

Рис. 11.53. Зависимость эффективности глушителя от числа камер и длины соединительной трубы

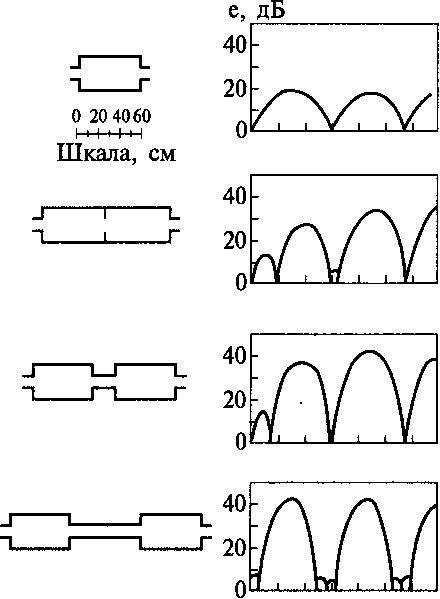
3. 20 4060

4. 11 11 11

Шкала, см

200 400 /, Гц

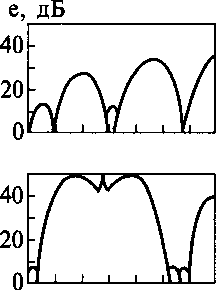
Рис. 11.54. Зависимость эффективности 200 400 / Гц глушителя от длины входного патрубка

источнику шума. На более высоких частотах, когда длина волны X равна или меньше поперечного размера камеры, эффективность бу­дет зависеть от других параметров (теоретически максимум эффек­тивности достигается при разности диаметров d₂ — d_x = Х/2, ЗХ/2, 5Х/2 и т. д.).

Эффективность е растет с увеличением числа камер и длины со­единяющей трубы. Однако уже добавление третьей камеры создает незначительный эффект по сравнению с двумя предыдущими (рис. 11.53).

На рис. 11.54 для сравнения показаны эффективность глушителя, состоящего из двух последовательных камер, и эффективность глу­шителя из двух камер, но со входом или выходом, введенным в полос­ти камер, и оканчивающимися на середине их длины. Эффектив­ность последнего глушителя выше. Изменяя длину входа и выхода, можно варьировать эффективность и частотный диапазон.

Если в спектре шума присутствуют дисперсные составляющие высокого уровня, то эффективность камерных элементов может ока­заться недостаточной. В этом случае применяют реактивные элемен­ты резонаторного типа: кольцевые и ответвления (рис. 11.55). Такой глушитель отличается от предыдущих тем, что поток газа через каме­ру не протекает, и она подсоединяется к основному трубопроводу че-

		V
	о — ft о о о о о о 4 ооооооо 1 / ■. / * /"Т>\ ч г—ч ▼ 1
		) Si S<r%St

d

Sn—XSi

St

a

б

Рис. 11.55. Схемы глушителей резонансного типа: а — кольцевые; б — ответвления

рез одно или некоторое количество небольших отверстий или трубок. Этот тип глушителя называют объемным резонатором или глушите­лем Гельмгольца. Резонансные частоты определяются размерами от­верстий и подсоединенным объемом. Предполагается, что линейные размеры подсоединенного объема меньше 1/10 длины волны на всех рассматриваемых частотах. Если это условие нарушается, то надо принимать во внимание движение волн в резонаторе. Ситуация ста­новится похожей на глушитель, рассмотренный выше. Эффектив­ность объемного глушителя

б = 10 lg{l + [а + 0,25]/[а² + р²(///о

-Л/Л²]},

где а = S_{z /S₀pc — безразмерное активное сопротивление резонатора; Р = S_{c/2nf₀V— безразмерное реактивное сопротивление резонатора; S_{ и S₀ — соответственно площадь трубопровода и суммарная пло­щадь отверстий; f_Q — резонансная частота; V— объем резонатора. При резонансе эффективность зависит только от величины а и

может быть записана в виде

е = 20 lg[(a + 0,5)/а].

При а < 0,25 и при частотах, намного больших или меньших час­тоты /о,

e=101g{l + l/[4 PV//0-/0//)²]}.

На рис. 11.56 показана эффективность глушителя рассматривае­мого типа при a = 0,5р.

Эффективность глушителя, синтезированного из типовых эле­ментов, может быть определена по формуле е ^{= У}£е_п где е_} — эффек­тивность /-го шумоглушащего элемента.

е

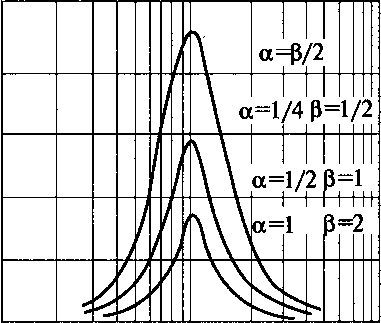
8 6 4 2 О

0,1 0,2 0,4 1 2 4 6ю/ю₀ Рис. 11.56. Эффективность резонаторного глушителя при а = 0,5р

Экранирование электромагнитных полей¹. Электромагнитное поле имеет зоны индукции и излучения, которые для элементарных излучате­лей (диполей) в воздухе определяются соответственно неравенствами:

X X

r«— (kr« 1) и г»— (kr>> 1),

2 71 2 71

где г — расстояние от источника. Обычно считают, что на расстоянии от источника, не большем длины волны,— зона индукции. Напри­мер, для частот 10⁹ и 10⁶ Гц расстояние, которое определяет зону ин­дукции, меньше 0,3 и 300 м.

Для антенн зону излучения обозначают неравенствами: г > 1²/Х и г > ЗА,, где / — размер антенны. В зоне излучения поле практически принимает плоскую конфигурацию и распространяется в виде пло­ской волны, составляющие которой равны:

Ё = Ё_те^Яш~^к*^х); ^(ПЛ05)

где с* ⁼ £ — уа/со — комплексная диэлектрическая проницаемость

среды; с и ju — абсолютные проницаемости соответственно диэлек­трическая и магнитная; а — удельная проводимость среды; ком­плексное волновое число к* = со ^/jus*.

Сравнивая выражения (11.54) и (11.105), видим, что импеданс среды электромаг­нитному полюсу z = / i. С учетом формулы (11.105) найдем, что для непроводящей

среды (а = 0)

= s; z = z> 5 = 0; (11.106)

для проводящей среды (е = 0)

^=V~Mia; z = yljaц/а; 5 = у = 7ю|ш/2 . (11.107)

В табл. 11.25 приведены ориентировочные значения волнового числа и импеданса

для металлов. Для вакуума импеданс равен ^ = 1— = 120 7г, Ом, где s₀ и — соответст-

V ⁸о

венно электрическая и магнитная постоянные: s₀ = 1/(Зб7г ♦ 10⁹) = 8,85 • Ю^-12 ф/м, (л₀ = 471 • 10"⁷ Гн/м. В зоне индукции импеданс среды зависит от источника.

Таблица 11.25. Характеристика металлов, применяемых для экранирования ЭМП

Металл	Электрическая проводимость а • 106, См/м	Магнитная про­ницаемость ц/ц0	Коэффициент распространения | &.|=^/соцст, мм	Импеданс \z*\=-J®n /сг, Ом
Медь	57,1	1	21,2 • 1<Г3 V7	0,372 • 10~6 77
Алюминий	34,5	1	16,4 • 10"3 V7	0,478 • 10"6 77
Сталь	7,2	100	75,4 • Ю-3 V7	10,47 • 10~6 77
Свинец	4,8	1	6,2 • Ю-3 V7	1,28 • Ю-6 77

При определении электромагнитного поля сложных источников их разбивают на элементарные, а затем используют принцип супер­позиции полей. Импеданс среды для поля элементарного электриче­ского излучателя

i = z*( 1 + jkr + \/jkr)/{\ +jkr). (11.108)

Импеданс среды для поля элементарного магнитного излучателя

i = z*( 1 + jkr)/(l+jkr + l/jkr). (11.109)

Из выражения (11.108) видно, что вблизи источника, т. е. в зоне индукции (kr« 1), импеданс среды преимущественно электриче­скому полю

z = z^E=z*/jkr. (11.110)

Импеданс среды преимущественно магнитному полю

z=z^H=jkrz*. (11.111)

Рис. 11.57. Импеданс среды для элементарных из­лучателей в зависимости от расстояния от источни­ка:

-11/2

1

\+{кг)

{кг)² {кг)²

/ — электрический диполь

\+{кг) [1 +{кг)²]

1 +{krf

- магнитныи диполь

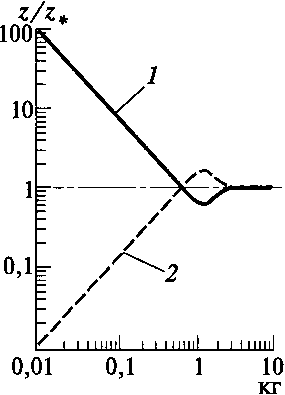
С увеличением расстояния от источника импеданс ^уменьшает­ся, а импеданс ^увеличивается (рис. 11.57). Оба импеданса будут стремиться к одному значению, которое они достигают в зоне излуче­ния (кг» 1 ):z=z^EH=z*.

Различают экранирование магнитного, электрического и элек­тромагнитного (плоская волна) полей. В большинстве случаев с двух сторон от экрана находится одна и та же диэлектрическая сре­да — воздух, и эффективность экранирования, пользуясь формулой (11.77), можно записать в виде

е = 20lg| chM+20lg|l+0,5(^2 /z_x+zjz₂ )thLh\. (11.112)

Чтобы произвести расчет по этой формуле, кроме толщины экра­на h необходимо знать коэффициент распространения к* и импедан- сы i\ и Z2- Так как экран обычно изготовляют из металла, то с учетом зависимостей (11.64) и (11.107) коэффициент распространения к* и

импеданс Zi будут равны: к* = 7 ; z = V-A⁰!¹¹2 /^а2 • Более слож­

но определяется импеданс z_x. В зоне излучения импеданс диэлектри­ческой среды — воздуха — будет равен (для воздуха ju - ju₀, е — е₀) z\ = z^{eh =} д/ilxj /е₁ ® д/jiio /е₀ ® 377 Ом. Однако в зоне индукции импе­данс i\ зависит не только от вида основной составляющей электро­магнитного поля [см. формулы (11.110) и (11.111)]. Он определяется также формой конструкции экрана (рис. 11.58). С учетом формы им­педанс i\ при экранировании электрического поля записывают в виде

Z\ = z\ = z*/jkinm = l/ycosinm, а при экранировании магнитного поля в виде

(11.113)

Шар

Цилиндр

Плоский экран

Рис. 11.58. Конструкции экранов

Zi = Z \ =jk_{r,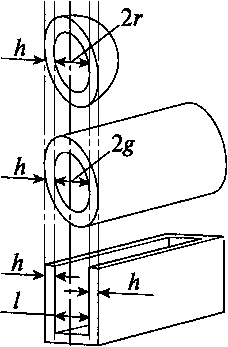

mz¹ =j(o\x\r_tm₉

где m = 2 при n = 1/2 для плоского экрана; т= 1 при п = р — для цилиндрического экрана; т = \/ы2 при п = г — для сфериче­ского экрана (см. рис. 11.58).

Тогда при k*h« 1, что обычно достига­ется на низр1х частотах (f< 10⁴ Гц), chk*h « 1, a thкМ « кМ и эффективность эк­ранирования электрического поля (Z^E\/Z2 > >

1

h

1 +

<101g

2m cdSj n

Эта эффективность будет большой на низких частотах, а в диапа­зоне относительно высоких частот е -> 0.

При экранировании магнитного поля необходимо учитывать осо­бенности материала, из которого изготовлен экран. Обычно для маг­нитных металлов (сталь, пермаллой, феррит) Zi/Z^H\> Z\/Zi, а для не­магнитных металлов (медь, алюминий, свинец) г \/zi > Zi/Z\. Тогда для защитных устройств из магнитных металлов эффективность эк-

1 \х₂ h

ранирования е « 20 lg

1+-

Она не зависит от частоты.

2т jlXj п

Для защитных устройств из немагнитных металлов е « 10 lg [1 + т

+ —ы\х_х<з₂гМ\ Эта эффективность зависит от частоты и при частоте

со ^ 0 тоже стремится к нулю.

В области относительно высоких частот (10⁴ </, Гц < 10⁹) эффек­тивность экранирования удобно определять* по формуле

е = +20 lg

1

4 у coju₂

Из соотношения импедансов следует, что амплитудные коэффи­циенты [формула (11.75)] для плоского Т_П9 цилиндрического Гц и сфе-

Рис. 11.59. Колебательный характер эффективности экранирования ЭМП в диа­пазоне СВЧ:

а — электрическое поле; б— магнитное поле; А, = 0,01 мм; h₂ = 0,001 мм; г=5 мм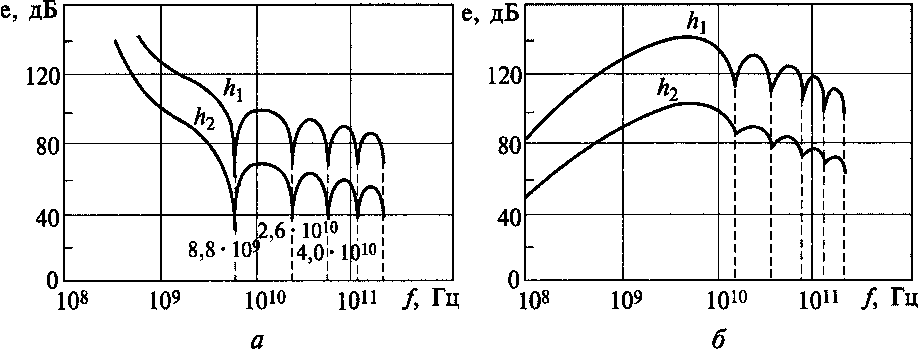

рического Г_с экранов при Zi > Z2 имеют приблизительно следующее соотношение: Г_п : Г_ц : Г_с = 1:2:3. Это соотношение справедливо для экранов, изготовленных из одинакового материала и имеющих равную толщину стенок, причем расстояние между параллельными пластинами плоского экрана равно диаметру сферического или ци­линдрического экранов (/= 2гили 2р). Таким образом, если эффек­тивность экранирования плоским экраном принять за исходное зна­чение е_п = 201g |1/Г_п |, то эффективность экранирования цилиндром е_ц = 201g |1 /Гц = 201g| 1/2Г_п| = е_п- 201g2 « е_п - 6 дБ, а эффективность экранирования сферой е_с = е_п — 9,5 дБ. При экранировании магнит­ного поля магнитными материалами (z₂ > zi) соотношение амплитуд­ных коэффициентов передачи будет иметь обратную закономерность Г_п: Гц : Г_с = 1 : 1/2 : 1/3. На практике полученными соотношениями пользуются при определении, например, эффективности цилиндри­ческого экрана по формулам плоского.

В области СВЧ, охватывающей дециметровые, сантиметровые и миллиметровые волны (f> 10⁹... 10^ю Гц), длина волны x соизмерима с диаметром экрана d, т. е. X > d, и эффективность экранирования но­сит колебательный характер (рис. 11.59). В этой области импеданс Zi при экранировании магнитного и электрического полей цилиндри­ческим экраном следует определять по формулам:

z? = z^ehjnk_xр/, (к_хр)н_х (к_{ р),| (11.114)

_zl^e =z^ehjnk_lpjl(k_lp)hl(k_lp),\

где J_n(u) и Н_п{и) — функции Бесселя¹ соответственно первого и третьего рода, порядка п (штрихом отмечены производные). С учетом соотношений (11.94) эффективность экранирования рассчитывают по формуле (11.92), при этом надо иметь в виду, что во многих случаях можно принять Z\/z₂ « 1 и пренебречь этим слагаемым.

При наличии в экране для радиоэлектронной аппаратуры отвер­стий или щелей, возникающих вследствие несовершенства его конст­рукции и технологии изготовления, среднюю эффективность экра­нирования можно определить по эмпирической формуле

e = 101g

л/2_Zl

+>4+8,6861?.

(11.115)

н Zx

где импеданс z_x ⁼ Z_{ при экранировании электрического поля; z_x при экранировании магнитного поля; импеданс \z₂\=\^j^2 /^а2 \

слагаемые А и множитель В = 2nh/l учитывают негерметичность эк­рана

А= 201g

г ~ V/³ 2 я

_кк_хп

(1-0,5 tl)⁶

где п - 0,62 И^/3 — эквивалентный радиус экрана любой геометриче­ской формы (V— внутренний объем экрана); / — наибольший размер отверстия (щели) в экране; к_х = со ^/ji₀e₀ • Формула (11.115) примени­ма в диапазоне частот, пока к_{1 <2, / > 0.

Для защиты от ЭМП обычно применяют металлические листы, которые обеспечивают быстрое затухание поля в материале. Однако во многих случаях экономически выгодно вместо металлического эк­рана использовать проволочные сетки, фольговые и радиопоглощаю- щие материалы, сотовые решетки.

Эффективность экранирования электрического поля при исполь­зовании проволочных сеток

е = lOlg \z^E/z | + >4 + 8,686С.

Здесь слагаемое А означает то же, что в выражении (11.115) (kj < 2), а множитель С и величину z при заданном диаметре провода d и шаге s сетки рассчитывают по формулам: С= nd/(s — d), Z = 1 /а₂Л*, где эквивалентная толщина сетки Л* = nc?/4s.

В сортамент фольговых материалов толщиной 0,01...0,05 мм входят в основном диамагнитные материалы — алюминий, латунь, цинк. Расчет эффективности экранирования фольговых материалов произ­водится по формулам для тонких материалов. При негерметичности эффективность экранирования электрического поля

е= lOlg + Л+ 11,9,

где z⁼ 1/сгй.

Радиопоглощающие материалы изготовляют в виде эластичных и жестких пенопластов, тонких листов, рыхлой сыпучей массы или за­ливочных компаундов. В табл. 11.26 приведены характеристики неко­торых радиопоглощающих материалов. В последнее время все боль­шее распространение получают керамикометаллические компози­ции.

Эффективность экранирования сотовыми решетками зависит вплоть до сантиметрового диапазона от отношения глубины к шири­не ячейки.

Таблица 11.26. Основные характеристики радиопоглощающих материалов

Марка поглотителя и материал, лежа­щий в его основе	Диапазон рабочих волн, см	Отражающая мощность, %	Размер пла­стины, м • 10~3	Масса 1 м2 материала, кг	Толщина материала, мм
СВЧ-068, фер­	15...200	3	100 х 100	18...20	4
рит
«Луч», древес­	15...150	1...3	600 х 1000	—	—
ное волокно
В2Ф2, резина	0,8...4	2	345 х 345	4...5	11...14
В2ФЗ : ВКФ1	0,8...4	4	345 х 345	4...5	(включая
					высоту
					шипа)
«Болото», по­	0,8...100	1...2	—	—	—
ролон

Ориентировочно эффективность

е « 27///_м + 20 lg л,

б

а

Рис. 11.60. Схема воздействия на роговицу глаза лазерного излучения: а — прямое облучение; б — диффузное излучение

где / и /_м — глубина и максимальный поперечный размер ячейки со­товой решетки; п — число ячеек.

Ослабление лазерного излучения светофильтрами. Если при пря­мом лазерном облучении невооруженного глаза (рис. 11.60) на по­верхность роговицы площадью пг* приходится энергия г, то энерге­тическая экспозиция Н= г/nrK. Как видно из рис. 11.60, а, расстоя­ние до расчетной точки ввиду малости угла у R= (г* — г)/у. Поэтому опасное расстояние

rJ 1/у ,

где Н* — допустимое нормами значение Н для роговицы глаза.

При облучении диффузным излучением, отраженным от площад­ки, которая характеризуется углом 0 (рис. 11.60, б) и коэффициентом отражения, опасное расстояние

R = tJps cos 0 / кН* .

При использовании для защиты светофильтра толщиной h коэф­фициент передачи через светофильтр т = е~^ън = 10~⁵\ где 8' и 8 = 8' In 10 — соответственно натуральный и десятичный показатели ослабления. В общем случае показатель ослабления светофильтра за­висит от толщины h и спектра излучения. Поэтому при расчете ослаб­ления пользуются оптической плотностью светофильтра D = lgl/x. Она связана с эффективностью защиты соотношением е = lOlg/^ = = lOlgl/т = 10D. Оптическую плотность D рассчитывают в зависимо­сти от характеристик излучения.