11.3.2. Защита от вибрации

Линейные вибросистемы состоят из элементов массы, упругости и демпфирования. В общем случае в системе действуют силы инер­ции, трения, упругости и вынуждающие.

Сила энерции, как известно, равна произведению массы Мна ее ускорение

d t

где v — виброскорость.

Сила /^направлена в сторону, противоположную ускорению.

Упругий элемент принято изображать в виде пружины, не имею­щей массы (рис. 11.35, а). Чтобы переместить конец пружины из точ­ки с координатой х₀ (ненапряженное соотношение) в точку с коорди­натой х_и к пружине необходимо приложить силу; при этом сила дей­ствия упругого элемента, или восстанавливающая сила, будет на­правлена в противоположную сторону и равна

F_g=Gx, (11.41)

где G — коэффициент жесткости, Н/м; х = х_{— х₀ — смещение кон­ца пружины, м.

При вибрации упругих систем происходит рассеяние энергии в окружающую среду, а также в материале упругих элементов и в узлах сочленения деталей конструкции. Эти потери вызываются силами трения — диссипативными силами, на преодоление которых непре­рывно и необратимо расходуется энергия источника вибрации.

рис. 11.35. Схематическое изо­бражение элементов упругости (а) и демпфирования (б)

Если рассеяние энергии происходит в элементе демпфирования (см. рис. 11.35, б), т. е. в вязкой среде (среде с вязким сопротивлени­ем), то диссипативная сила F_s пропорциональна виброскорости и но­сит название демпфирующей:

F_s = Sv. (11.42)

Сила F_s всегда направлена против скорости, коэффициент S{Н с/м) называют импедансом, или сопротивлением элемента демпфирова­ния.

Основные характеристики виброзащитных систем. К основным ха­рактеристикам виброзащитных систем отнесены собственная частота системы, механический импеданс и коэффициенты, определяющие процессы затухания вибраций и рассеяния энергии¹.

По аналогии с формулой (11.42) можно ввести общее понятие ме­ханического импеданса материальной точки при гармонической виб­рации

z = F/y или \z\=\F/% где комплексное число z в полярной форме можно записать в виде

Найдем импеданс элементов массы и упругости. При заданной виброскорости v смещение х и ускорение а материальной точки находят интегрированием и дифферен­цированием:

\ = \_те^,ш; x = v / (усо); а= /иv. (11.43)

13*

387

Об - M

Ft

„ Fa

\,

Fs

Fm

F₀

Рис. 11.36. Схема вибро­системы с одной степе­нью свободы

Подставив ускорение а в формулу (11.40), определя­ют импеданс элемента массы, или просто импеданс мас­сы z_M\

_rdv

(11.44)

F_M=M—- = j<*M = z_M v. at

Таким образом, импеданс массы z_M является

мнимой положительной величиной, пропорциональной частоте. Он достигает больших значений в диапазоне высоких частот. В диапазоне низких частот им можно пренебречь.

Подставив смещение х в формулу (11.41), находят импеданс элемента упругости z_G'

(11.45)

- Gx = — v = z_G v . >

Таким образом, импеданс элемента упругости z_G = -j— является чисто мнимой

со

отрицательной величиной, обратно пропорциональной частоте; в области высоких частот им можно пренебречь.

Импеданс элемента демпфирования является действительной величиной

Z_s = S\ F_s = i_sy.

В общем случае вибросистему с одной степенью свободы можно изобразить в виде элемента массы, не обладающего деформацией, и элементов упругости и демфирова- ния, не имеющих массы (рис. 11.36). Точка О обозначает положение статического рав­новесия, от которого отсчитывается смещение jc тела массой М под действием гармо­нической вынуждающей силы F_r К телу также приложены сила инерции F_M, восстанав­ливающая сила F_g и диссипативная демпфирующая сила F_s. В соответствии с принци­пом Д'Аламбера

F_u+F_n+F,= F_f.

(11.46)

Свободная вибрация (F_t = 0) в отсутствие сил трения (F_s = 0) с течением времени не затухает. Виброскорость в этом случае определяется выражением (11.43), в котором амплитуда v_m = const. Условие F_M + F_G = 0c учетом выражений (11.44) и (11.45) позво­ляет определить собственную частоту вибросистемы:

со ₀=jG/M.

Собственную частоту системы с одной степенью свободы (см. рис. 11.35, а) на практике определяют по прогибу А, исходя из равенства сил F_G = F_M в статике:

со₀ М = yjg/А ,

где g — ускорение свободного падения.

При наличии сил трения (F_s ф 0) свободная вибрация (F_t = 0) затухает. Амплитуда виброскорости с течением времени убывает. Чтобы учесть это, вводят комплексную уг­ловую частоту со, = со₀. +у8, где 8 — коэффициент демпфирования. Поставив в выраже­ние (11.43) частоту со. вместо со, получим

v = у_{ш е}-^{ф v)} = у_т (8)e^/(<Bo*'^+(Pv), (11.47)

где v_m(8) = v_me ^5t — амплитуда виброскорости с учетом затухания.

Из уравнения F_M+ F_G + F_s= (j й>,М—jG/<Ь„ + S)\ = 0 находят неизвестные вели­чины 8 и оа₀..

5 = S/2M,

k	1-	/ \ S	2~
\м		Ар у

где 5_кр = 2 4GM — критический импеданс элемента демпфирования.

Таким образом, коэффициент демпфирования равен половине импеданса эле­мента демпфирования, приходящегося на единицу массы, и свободная вибрация с за­туханием осуществляется с частотой ю₀„ зависящей от отношения импедансов S/S_Kp, которое характеризует силы трения в системе. При отсутствии диссипативных сил (S/S_Kp = .0) частота оэ₀. = оэ₀; если же диссипативные силы имеют критическое значение, т. е. если S/S_Kp = 1, то частота оэ₀. = 0.

Вынужденная вибрация (F_{ * 0) происходит с частотой ю вынуж­дающей силы. Из уравнения (11.46) определяют механический импе­данс вибросистемы:

z= S + j(oM-jG/(o. (11.48)

Таким образом, импеданс вибросистемы складывается из импе­дансов элемента демпфирования, массы и упругости. Он имеет ак­тивную и реактивную составляющие. Его модуль и фазовый угол рав­ны:

z Н % = <sJ$²+(c*M-G/G))², (11.49)

<p_z = arctg[(o)M— G/co)/S\.

Как следует из соотношения (11.49), импеданс вибросистемы имеет минимальное значение на частоте ю = со₀, при которой слагае­мое в круглых скобках обращается в нуль, т. е. в резонансной области импеданс вибросистемы определяется импедансом элемента демп­фирования (z = S). Вне резонансной области импедансом S можно пренебречь. Тогда из выражения (11.48) следует, что в диапазоне вы­соких частот движение определяется вибрирующей массой (z « jcoM), а в диапазоне низких частот — жесткостью системы (z ® — y'G/©).

Защитное устройство — упругодемпфирующий элемент. В боль­шинстве случаев расчет сложных защитных устройств сводится к рас­чету простого защитного устройства, состоящего из элемента упруго­сти и элемента демпфирования, соединенных параллельно. Реакция

	< F(x,v)
f
с	У/

Рис. 11.37. Рассея­ние энергии — гистерезисная пет­ля

(11.50)

защитного устройства складывается из реакций уп­ругого и демпфирующих элементов F_R = F_G + F_s• Импеданс защитного устройства

Zr = ZS+ ZG= (S-jG/co).

Если провести циклическое деформирование уп- ругодиссипативного элемента по закону х = x_wcosoo^ то обнаруживается различие линий нагрузки и раз­грузки (рис. 11.37) на диаграмме сила — смещение: точка, изображающая напряженное и деформиро­ванное состояние, описывает замкнутую кривую — петлю гистерезиса. Площадь, ограниченная петлей гистерезиса, вы­ражает энергию е_Л рассеянную за один цикл демпфирования и рав­ную работе диссипативных сил:

т

£s ⁼ §F_r(x, v)dx = Ji^ (v)vdf = nx¹_m(o3.

В начале и конце цикла деформирования смещения максималь­ны, виброскорость равна нулю и вся энергия, запасенная системой, равна потенциальной:

£(}⁼ $^с?(.х)ск = Gx/2 = scos²(ot; г = Gx_m/2.

По формуле (11.38) находят коэффициент потерь и преобразуют его с учетом выражения для критического импеданса:

(о$ 1 S со ~G

Г| = -

Тогда выражение (11.50) можно записать в виде

. G _{( л} со

(11.51)

Виброизоляция. Между источником вибрации и ее приемником, являющимся одновременно объектом защиты, устанавливают упру- годемпфирующее устройство — виброизолятор — с малым коэффи­циентом передачи (рис. 11.38, а). Схематично система «источник вибраций — защитное устройство — приемник» показана на рис. 11.38, б. При возбуждении системы защитное устройство, располо­женное между источником и приемником, воздействует на них с ре­акциями F_r и Fr. Ниже будут рассматриваться только безынерцион­ные устройства, у которых реакции F_R и Fr равны. 390

Рис. 11.38. Виброизоляция:

а — устройство виброизоляции (1 — источник; 2 — виброизолятор; 3 - б — схема системы И — зу — П

приемник);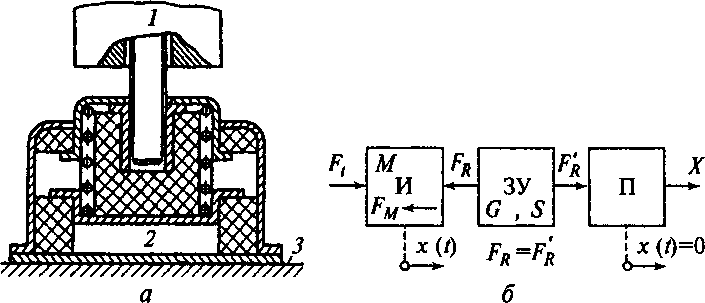

Различают два вида возбуждения: силовое и кинематическое; при этом соответственно большую массу имеет приемник и его считают неподвижным или источник и закон его движения считают задан­ным.

При силовом гармоническом возбуждении силой F_t = F_m цель защиты обычно состоит в уменьшении амплитуды силы F_R, переда­ваемой на приемник. Импеданс виброизолятора определяется фор­мулой (11.51). Импеданс вибросистемы

Z — Z_M +Z_R

G

(О

Л+J

Г 2 СО

ч°>0

-1

Поток энергии на входе в ЗУ определяется усредненной за цикл мощностью вынуждающей силы [3]:

Поток энергии на выходе из защитного устройства определяется усредненной за цикл мощностью реакции защитного устройства [3]:

Отношение мощностей W^/JV" называют силовым коэффици­ентом защиты k_F = z/zr- Из соотношений F_t =zv и F_R =z_Rv видно, что он при определенных условиях равен отношению амплитуды вынуж­дающей силы к амплитуде силы, переданной на приемник.

При кинематическом возбуждении цель защиты обычно заключа­ется в уменьшении передаваемого смещения. Степень реализации

этой цели характеризуют динамическим коэффициентом защиты к_х, равным отношению амплитуды смещения источника к амплитуде смещения приемника. Можно показать, что к_х = z/Zr.

В общем случае энергетический коэффициент защиты можно вы­разить в виде k_w = k_Fk_x.

По формуле (11.39) эффективность виброизоляции

e = mgk_w -201g

z

(11.52)

Zr

В области высоких частот импеданс z ® Z_M (см. выше) и эффек­тивность виброизоляции равна е « 401gw/wo — 101g(l + л²).В частно­сти, если демпфирующее сопротивление мало влияет на движение системы, то величиной г| можно пренебречь. Тогда е = 401go)/o)o, т. е. в области высоких частот почти вся энергия затрачивается на движение массы; поток энергии, передаваемой на приемник, обратно пропор­ционален квадрату частоты возбуждения, и эффективность виброи­золяции тем выше, чем больше частота со.

В области низких частот z « Z_G и эффективность виброизоляции 101g(l + г|²), т. е. отрицательна или равна нулю.

В общем случае из выражения (11.52) следует, что эффективность виброизоляции

е = lOlgh² + (ш²/о²о - I)²] - 101g(l + л²)-

Если потери в защитном устройстве отсутствуют (г| = 0), то эф­фективность

е = 201g(a>²/a>o — 1).

Из последнего выражения видно, что цель виброизоляции (е > 1) обеспечивается в частотном диапазоне: со > л/2со₀ .

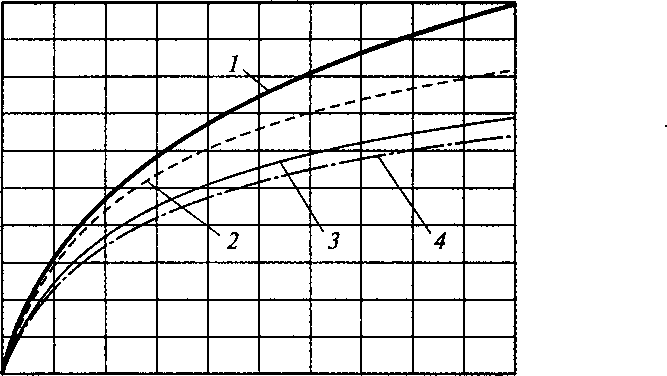
На рис. 11.39 представлены коэффициент виброизоляции т и эф­фективность виброизоляции е в зависимости от отношения частоты вынуждающей силы к собственной частоте вибросистемы при разных значениях отношения импеданса демпфирующего элемента к его критическому значению.

т

	//	\\ *	1
	// //	VI \\	-2
		\ Л - vA	-3
				"V \

О 0,5 1 1,5 2 2,5 3

©/©о

В качестве виброизоляторов используют упругие материалы и прежде всего металлические пружины, резину, пробку, войлок. Вы­бор того или иного материала обычно определяется величиной тре­буемого статического прогиба и условиями, в которых виброизолятор) будет работать (например, температурой, химической агрессивно- а

е, дБ 40 36 32 28 24 20 16 12 8 4 0

1,41 2,27 3,13 3,99 4,85 5,71 6,56 7,42 8,28 9,14 10

<о/со₀

б

Рис. 11.39. Коэффициент виброизоляции т= 1 /k_F (а) и эффективность виброизоля­ции е (б) в зависимости от отношения частот и при значениях отношения S/S_Kp\ кривая 7 — 0; кривая 2—0,4; кривая J — 0,8; кривая 4—1

стью рабочей среды и т. д.). Зависимость между статическим проги­бом и собственной частотой для некоторых материалов показана на рис. 11.40.