2.1.2. Погрешности и методы обработки результатов измерения

Результаты измерения физической величины дают лишь приближенное ее значение. Отклонение результата измерения от истинного значения измеряемой величины называют погрешностью измерения. Погрешности средства измерения классифицируются по признакам, приведенным на рис. 2.2.

Погрешность измерения в общем случае определяется погрешностью средств измерений и погрешностью измерений этими средствами [2].

Погрешность средства измерения, используемого в нормальных условиях (нормальное положение прибора, температура 20 ± 5° С, отсутствие внешних полей и т. п.), называется основной погрешностью измерений. Изменение погрешности, вызванное отклонением одной из влияющих величин от нормального значения или выходом ее за пределы нормальной области значений, называется дополнительной погрешностью средств измерений.

Погрешность измерений выражают в виде абсолютных и относительных величин. Различают следующие погрешности средств измерения:

а) абсолютную погрешность

х = х_п – х_д, (2.1)

где х_п – показания прибора; х_д – действительное значение измеряемой величины;

б) относительную погрешность, выражаемую в процентах,

δ = (∆х/х_д)100, (2.2)

где x – абсолютная погрешность;

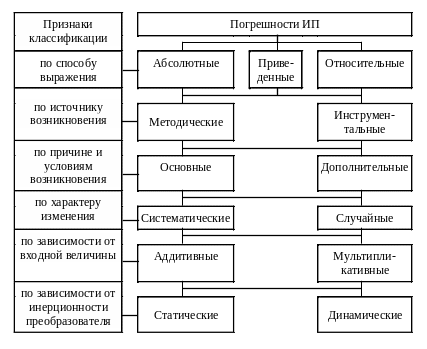
Рис. 2.2. Классификация погрешностей средств измерения.

в) приведенную погрешность, также выражаемую в процентах,

γ = х/х_н.з, (2.3)

где х_н.з – нормирующее значение, т. е. некоторое установленное значение, по отношению к которому рассчитывается погрешность (часто в качестве нормирующего значения для приведенной погрешности принимают предел измерения прибора).

Обобщенной характеристикой средств измерений, определяемой пределами допускаемых основных и дополнительных погрешностей, а также другими свойствами указанных средств, влияющими на их точность, значения которых устанавливаются в стандартах на отдельные виды средств измерений, является класс точности.

В нашей стране используются два вида классов точности: по абсолютным погрешностям и по приведенным относительным, или относительным, погрешностям. В последнем случае класс точности – это число, совпадающее с пределом допускаемой погрешности, соответствующим конечному значению рабочей части шкалы. Приняты следующие классы точности средств измерения: 1; 1,5; 2; 2,5; 4; 5 и 6. Эти числа ряда могут быть умножены на 10ⁿ, где n = – 1, 0, – 1, – 2. . . Например, прибор класса 0,5 может иметь основную приведенную погрешность, не превышающую 0,5%, и удовлетворять соответствующим требованиям в отношении допускаемых дополнительных погрешностей.

Рассматривая средства измерения как преобразователи входной величины X в выходную Y, следует отметить, что в действительности выходная величина Υ зависит также и от ряда влияющих величин x₁, x₂, . . . , x_n, т. е. Υ = f (x, x₁, x₂, . . . , x_n).

Полный дифференциал Υ

(2.4)

Частные производные в правой части уравнения (2.4) являются чувствительностью S прибора (преобразователя) к входной и к влияющим величинам, которые определяют дополнительную погрешность средства измерения:

(2.5)

Тогда

(2.6)

Из выражения (2.6) видно, что влияющие величины не будут вызывать дополнительной погрешности, если или

Для реализации этих требований отдельные виды средств измерений снабжают дополнительным устройством, позволяющим в процессе измерений периодически проверять градуировку. Одним из путей уменьшения дополнительных погрешностей является увеличение S_х по сравнению с чувствительностью к влияющим величинам.

Как правило, нормированные дополнительные погрешности от каждой влияющей величины х_i не должны превышать основной погрешности средства измерения.

Оценка точности результата измерений, т. е. определение погрешности, имеющей при этом место, – одна из основных задач измерений. При проведении измерений желательно получить значение измеряемой величины с заданной точностью или, иначе говоря, необходимое количество информации, являющееся мерой уменьшения неопределенности измеряемой величины.

Величина Δ, обратная модулю относительной погрешности, называется точностью измерения. Например, если относительная погрешность равна 10^‑5, то точность A = 10⁵.

В общем случае погрешность, измерения представляет собой нестационарную случайную величину, которую можно представить в виде

x = Μ[x] + δ, (2.7)

где Μ[x] – математическое ожидание погрешности;  – стационарная центрированная случайная величина.

Математическое ожидание погрешности измерения принято называть систематической погрешностью, а ее центрированную случайную составляющую – случайной погрешностью. Систематическая погрешность при повторных измерениях одной и той же величины остается постоянной или закономерно изменяется. Случайная погрешность при повторных измерениях одной и той же неизменной по значению величины изменяется по значению и знаку случайным образом и зависит от носящих случайный характер изменений условий эксперимента и параметров средств измерения.

По природе возникновения отдельные погрешности измерений могут быть разделены на инструментальные, методические, погрешности установки и считывания. Все эти погрешности могут содержать как систематические, так и случайные составляющие.

Инструментальные погрешности обусловлены конструктивными и технологическими недостатками используемых средств измерения. Например, погрешность от неправильной градуировки шкалы прибора – систематическая для данного прибора, а погрешность от трения в его опорах – случайная.

Инструментальная погрешность меры содержит систематическую составляющую из-за неточности ее изготовления и случайную составляющую от нестабильности ее элементов.

Методические погрешности появляются из-за несовершенства метода измерений или допущенных упрощений при определении зависимостей, положенных в основу метода измерений Характерной методической погрешностью является, например, погрешность обусловленная потреблением приборами мощности что зависит от конечных значений сопротивлений цепей самих приборов.

Погрешности установки вызываются отклонением условий измерении от нормальных условий, т. е. тех условий, при которых производились градуировка и проверка средств измерений. Сюда относятся, например, погрешности от неправильной установки прибора в пространстве или его указателя на нулевую отметку от влияния рядом расположенных приборов, изменения температуры внешних электромагнитных полей, напряжения питания частоты.

Погрешности считывания зависят от вида отсчетного устройства и субъективных особенностей экспериментатора (например, погрешности из-за запаздывания реакции экспериментатора или от неточного отсчета долей деления по шкале прибора). Эти погрешности отсутствуют при использовании цифровых приборов.

Систематические погрешности можно исключить или уменьшить, устранив, прежде всего, причины их появления. Другим радикальным способом исключения систематических погрешностей является поверка средств измерений перед их применением в аналогичных условиях с целью определения поправок к результатам измерения которые имеют вид таблиц или графиков поправок Наряду с общими методами исключения систематических погрешностей при меняют также специальные методы: метод замещения измеряемой величины равновеликой ей известной величиной, метод компенсации погрешности по знаку, метод симметричных наблюдений и т. д. Случайные погрешности в отличие от систематических нельзя учесть с помощью поправок и исключить в процессе измерения так как при каждом повторном наблюдении они принимают новые значения. Их влияние на результат измерения можно уменьшить путем проведения многократных наблюдений.

Если все систематические погрешности исключены то случайная погрешность представляет собой центрированную случайную величину с математическим ожиданием, равным нулю Случайная погрешность i-го результата измерений x_i может быть представлена как

_i = x_i – М[х], (2.8)

где Μ[x] – математическое ожидание измеряемой величины относительно которого рассеиваются результаты измерений и которое при отсутствии систематических погрешностей принимается за истинное значение измеряемой величины.

Наиболее полной характеристикой случайных погрешностей, как, и любой случайной величины, является закон распределения их вероятностей, определяющий возможные значения случайных погрешностей и вероятность их появления.

На рис. 2.3 показаны некоторые наиболее распространенные законы распределения погрешностей: нормальный (а), равномерный (б), трапецеидальный (в); треугольный (г) и в виде двух -функций (д). Ординаты кривой закона распределения P () соответствуют плотности вероятности случайных погрешностей , значения которых отложены по оси абсцисс. Вероятность того, что случайная погрешность будет лежать в пределах от ₁ до δ₂, определяется площадью, ограниченной вертикалями, проведенными через точки ₁ и ₂ (заштрихованная площадь на рис. 2.3, а).

Довольно часто случайные погрешности подчиняются нормальному закону распределения вероятностей. Это объясняется тем, что многие случайные погрешности являются результатом совместного действия большого числа случайных независимых причин, каждая из которых вносит примерно одинаковый вклад в общую погрешность.

Закон распределения суммы двух независимых случайных погрешностей [9], каждая из которых распределена по равномерному закону (см. рис. 2.3, б), в общем случае имеет вид трапеции (см. рис. 2.3, в). Как частный случай, композиция двух одинаковых равномерных распределений представляет собой треугольное распределение (см. рис. 2.3, г). Погрешности, обусловленные гистерезисом, подчиняются закону распределения в виде двух -функций, когда имеют место погрешности, равные только +Δ и –Δ (см. рис. 2.3, д), а другие погрешности не встречаются.

Наиболее важным параметром распределения случайных погрешностей является дисперсия σ² или среднее квадратическое отклонение σ. Дисперсия представляет собой математическое ожидание квадрата случайных погрешностей и характеризует разброс результатов измерений из-за наличия случайных погрешностей

(2.9)

а б в г д Рис. 2.3. Законы распределения погрешностей

На практике удобнее пользоваться средним квадратическим отклонением , определяемым как положительный корень квадратный из дисперсии и имеющим такую же размерность, что и сама случайная погрешность.

Границы доверительного интервала, за пределы которого с заданной вероятностью P не выходят случайные погрешности, обычно выражают в долях от σ:

(2.10)

где K – безразмерный коэффициент, определяемый задаваемой вероятностью P и видом закона распределения вероятностей случайных погрешностей.

Статистическая оценка погрешности. Практически для определения погрешности получают конечный ряд из n наблюдений, по которому можно найти только приближенную оценку среднего квадратического отклонения σ. Такой эмпирической оценкой σ является эмпирическое среднее квадратическое отклонение

(2.11)

где x_i – результат i-го наблюдения; – среднее арифметическое значение результатов наблюдений, являющихся оценкой математического ожидания Μ[x] измеряемой величины.

После того как по результатам наблюдений получены данные, можно построить приближенный график закона распределения погрешностей – гистограмму распределения. По виду гистограммы можно подобрать для нее близкий теоретический закон распределения, для которого известны аналитические функции плотности вероятности. Пользуясь этими функциями или уже имеющимися таблицами, можно определить коэффициент K для заданной вероятности Р.

Например, если по виду гистограммы можно сделать заключение, что случайные погрешности подчиняются равномерному закону распределения вероятностей, то зависимость между Δ и σ определяется следующим образом. Аналитически равномерное распределение случайной величины можно представить так:

Тогда

откуда

В этом простейшем случае по значению σ и коэффициенту K = 1,73 определяют границы интервала возможных значений случайных погрешностей, которые равномерно распределены в этом интервале.

Аналогичным образом можно определить границы интервала возможных значений случайных погрешностей для различных законов распределения вероятностей.

На практике чаще всего, если неизвестен закон распределения вероятностей случайных погрешностей, принимают нормальный закон распределения. Аналитически нормальное распределение описывается функцией

, (2.12)

где – плотность вероятности погрешности ;

– среднее квадратическое отклонение погрешности;

– систематическая составляющая погрешности.

Вид нормального закона распределения для двух значений  представлен на рис. 2.4.

Так как случайная погрешность , то закон распределения случайной составляющей погрешности описывается выражением, аналогичным, т.е.

где – среднее квадратическое отклонение случайной составляющей погрешности; .

Тогда выражения математического описания и дисперсии можно записать в следующем виде:

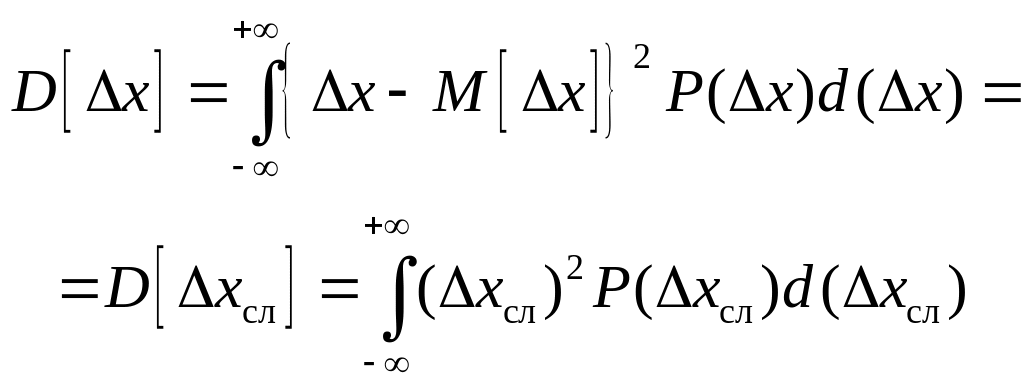
Рис. 2.4. Вид нормального закона распределения при различных 

Нормальному закону распределения присущи свойства симметрии и монотонного убывания плотности вероятности. Это означает, что при очень большом числе измерений появление случайных погрешностей, равных по значению, но разных по знаку, равновероятно. При этом малые погрешности встречаются чаще, чем большие, а появление больших случайных погрешностей маловероятно.

В зависимости от величины погрешности средств измерения разделяют на мультипликативные и аддитивные.

Мультипликативные погрешности возникают при изменении коэффициента преобразования средств измерения под воздействием внешних и временных факторов, что вызывает изменение чувствительности S. Обычно мультипликативные погрешности изменяются пропорционально измеряемой величине.

Аддитивные погрешности не зависят от измеряемой величины и характеризуются дрейфом «нуля», наложением помех на выходной сигнал и другими факторами, что приводит к смещению характеристики измерительных устройств.