1.4.2. Теоретичні засади процесу фільтрування

Швидкість фільтрування. Швидкістю фільтрування W називають кількість фільтрату V, яка проходить через одиницю поверхні фільтра S за одиницю часу τ.

Враховуючи, що під час фільтрування швидкість процесу в кожний конкретний момент часу прямо пропорційна до різниці тисків і обернено пропорційна до в’язкості рідкої фази, до загального гідравлічного опору шару осаду і до фільтрувальної перегородки, які з часом змінюються, змінну швидкість фільтрування виражають у диференціальній формі:

(1.34)

або відповідно до викладеного основного диференціального рівняння вона має вигляд:

; (1.35)

де V – об’єм фільтрату, м³; S – поверхня фільтрування, м²; τ – тривалість фільтрування, с; ΔР – різниця тисків, Па; µ – в’язкість рідкої фази суспензії, Пас; R_о – опір шару осаду; R_фп – опір фільтрувальної перегородки.

З рівняння (1.35) очевидно, що величини R_о і R_фп мають розмірність м^-1. Опір фільтрувальної перегородки R_фп, нехтуючи деяким його збільшенням унаслідок проникнення в пори твердих частинок, можна вважати приблизно сталим. Опір осаду R_о із зростанням висоти шару змінюється від нуля на початку фільтрування до максимального значення наприкінці процесу. Позна­чимо через х_о відношення об’єму осаду до об’єму фільтрату. Тоді об’єм осаду дорівнюватиме х_о V. З іншого боку, об’єм осаду дорівнює h_о S, де h_о – висота шару осаду в м. Отже,

, (1.36)

звідки товщина шару осаду на фільтрувальній перегородці:

_. (1.37)

Позначимо через r_o питомий об’ємний опір шару осаду, м^-2. Тоді опір шару з урахуванням (1.37) становитиме:

_. (1.38)

З рівняння (1.38) очевидно, що величина r_o характеризує опір потокові рідкої фази шаром осаду завтовшки 1 м.

Запишемо рівняння (1.35), підставляючи у нього значення R_о з рівняння (1.38):

. (1.39)

Якщо нехтувати опором фільтрувальної перегородки (R_фп = 0) і врахувати (1.37), то з рівняння (1.39) знайдемо:

. (1.40)

Якщо µ = 1 Пас, h_о = 1 м і W = 1м/с, то величина r_о = ΔР. Отже, питомий опір осаду чисельно дорівнює різниці тисків, яка необхідна для того, щоб рідка фаза в’язкістю 1 Пас фільтрувалась зі швидкістю 1 м/с через шар осаду завтовшки 1 м. На початку фільтрування, коли на фільтрувальній перегородці ще не утворився шар осаду, об’єм фільтрату V = 0. Тоді з рівняння (1.39) отримаємо:

. (1.41)

Якщо прийняти µ = 1 Пас і W = 1 м/с, отримаємо величину R_фп = ΔР. З цього очевидно, що опір фільтрувальної перегородки числово дорівнює різниці тисків, яка необхідна для того, щоб рідка фаза в’язкістю 1 Пас проходила через фільтрувальну перегородку зі швидкістю 1 м/с. Для деяких фільтрувальних перегородок величина R_фп має порядок 10¹⁰ м^-1.

Як зазначали раніше, на практиці фільтрування можна здійснювати або за сталої різниці тисків, або за сталої швидкості. Відповідно розрізняють режим сталої різниці тисків і режим сталої швидкості.

Рівняння фільтрування за постійної різниці тисків. Для режиму постійної різниці тисків (ΔР = соnst) усі величини, що входять в рівняння (1.39), за винятком V і τ, сталі. Проінтегруємо це рівняння в межах від 0 до V і від 0 до τ:

(1.42)

або

_.

Розділимо обидві частини останнього рівняння на µr_ох_о/2S і остаточно отримаємо:

. (1.43)

Розв’язуючи це рівняння відносно V, отримаємо залежність об’єму фільт­рату від тривалості фільтрування. Це рівняння можна використовувати, коли осад стисливий і коли не стисливий, оскільки величини r_o і х_о за ΔР = const також сталі.

З рівняння (1.43) очевидно, що за ΔР = const із збільшенням об’єму фільт­рату, звідси і тривалості фільтрування, швидкість фільтрування зменшується.

Якщо заданий необхідний об’єм фільтрату V, то з рівняння (1.43) очевидно

. (1.44)

Тобто, для режиму фільтрування за сталої різниці тисків тривалість фільтрування пропорційна до квадрату об’єму фільтрату.

Рівняння фільтрування за сталої швидкості фільтрування. Для цього режиму маємо:

. (1.45)

Розв’язуючи рівняння (1.39) відносно ΔР, знайдемо:

. 1.46)

Рівняння (1.46) виявляє, що для режиму фільтрування зі сталою швид­кістю різниця тисків зростає із збільшенням тривалості фільтрування.

Рівняння (1.46) можна застосовувати для нестисливих осадів. У разі ви­користання його для стисливих осадів необхідно мати на увазі залежність питомого опору осаду від різниці тисків.

Рівняння фільтрування за сталої різниці тисків і сталої швидкості. Такий режим фільтрування здійснюється тоді, коли чиста рідина фільтрується через шар осаду постійної товщини за постійної різниці тисків. Прикладом такого режиму є промивання осаду на фільтрі способом витіснення.

Проаналізуємо рівняння (1.39). З урахуванням (1.37) і, приймаючи в рівнянні (1.39) замість dV/dτ V/τ = const , за умови, що ΔР = const, знайдемо:

. (1.47)

Це рівняння виявляє залежність об’єму фільтрату від тривалості фільтру­вання чистої рідини. Оскільки в розглянутому режимі фільтрування ΔР = const, рівняння (1.47) можна використовувати як для нестисливих, так і для стис­ливих осадів.

Визначення сталих у рівняннях фільтрування. Під сталими у рівнян­нях фільтрування (1.43), (1.46) і (1.47) розуміють відношення об’єму осаду до об’єму фільтрату х_о, питомий об’ємний опір осаду r_о та опір фільтрувальної перегородки R_фп. Під час розрахунків процесу фільтрування ці величини одержують експериментально. На лабораторному фільтрі за умови ΔР = const за певні проміжки часу фіксують об’єм фільтрату, вимірюють висоту шару осаду і потім обробляють отримані результати графічним методом. Розглянемо детальніше цей спосіб.

Запишемо рівняння (1.43) у вигляді:

(1.48)

або

; (1.49)

де

, (1.50)

(1.51)

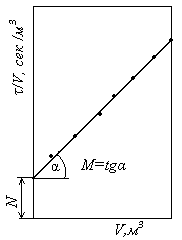
Рис. 1.10. До визначення питомого опору осаду і опору фільтрувальної перегородки

За постійних температури й різниці тисків усі складові, які входять у праві частини рівнянь (1.50) та (1.51), сталі. Тому величини М і N також сталі, і рівняння (1.49) є рівнянням прямої лінії, нахиленої до горизонтальної осі під кутом, тангенс якого дорівнює М, а відрізок на осі ординат, який відтинає пряма, дорівнює N. Для побудови вказаної прямої у координатах V – τ/V наносять ряд точок (рис. 1.10), які відповідають виміряним у дослідах значенням V і τ. Тоді за графіком визначають величини М і N, після чого за виразами (1.50) і (1.51) розраховують r_o і R_фп. Величину х_о знаходять після безпосереднього вимірювання об’ємів осаду й фільтрату.