Перемішування в рідкому середовищі

36. Критерії гідродинамічної подібності для процесу перемішування виз­начають так. Критерій Рейнольдса (відцентровий):

. (3.44)

Критичне значення цього критерію:

Rе_{ц. кр}  50.

Критерій потужності:

. (3.45)

У літературі іноді називають відцентровим критерієм Ейлера і позначають Еu_ц^.

Критерій Фруда (відцентровий):

, (3.46)

де N – потужність, споживана мішалкою, Вт;  – густина рідини, кг/м³;  – динамічний коефіцієнт в’язкості рідини, Пас; n – частота обертання мішалки, с^-1; d – діаметр мішалки, м; g = 9,81 м/с² – прискорення вільного падіння.

37. Критерійне рівняння для розрахунку потужності, споживаної мішал­кою, у загальному вигляді:

.

Зазвичай впливом сили тяжіння нехтують. Тоді :

,

де – cимплекс геометричної подібності, що характеризує конструкцію мішалки, вплив висоти шару рідини та інші геометричні чинники; d – діаметр мішалки, м; D – діаметр посудини, м; b – ширина лопаті мішалки, м; Н₀ – висота шару рідини, м.

Для геометрично подібних апаратів з мішалками узагальнене критеріаль­не рівняння набуває вигляду:

, (3.47)

де с і т – сталі величини (для такої конструкції мішалки і для певного режиму перемішування).

Значення сталих величин c і т у загальному рівнянні (3.47) для різних мішалок наведено в табл. XXI [2]; на рис. VII показано залежність К_N = f (Rе_ц) для цих мішалок.

Приклади задач та їх розв’язування Осадження

Приклад 3.1. Знайти верхню межу (тобто найбільший діаметр частинок) застосування формули Стокса до частинок кварцу густиною 2650 кг/м³, що осідають у воді за температури 20 °С.

Розв’язання. Формула Стокса застосовна тільки за Аr < 3,6. Тому найбільша частинка кварцу, осадження якої можна розрахувати за формулою Стокса, повинна мати діаметр:

Приклад 3.2. Знайти швидкість осадження у воді частинок кварцового піску кулястої форми діаметром 0,9 мм, якщо густина піску – 2650 кг/м³, а температура води – 20 °С.

Розв’язання. Визначаємо критерій Аr:

де для води _с = 110^-3 Пас (табл. 2 додатка).

За значенням Аг = 1,1810⁴ . З рис. 3.1 знаходимо Rе = 140.

Швидкість осадження частинок кварцового піску кулястої форми діамет­ром 0,9 мм визначаємо з виразу:

м/с.

Приклад 3.3. Знайти швидкість осадження у воді за температури 20 °С частинки свинцевого блиску неправильної форми з d_e = 1 мм. Густина свинцевого блиску – 7560 кг/м³.

Розв’язання. Швидкість осадження частинок неправильної форми знайде­мо з критерію Lу, заздалегідь визначаючи значення критерію Аr:

де _с = 110^-3 Пас (табл. 2 додатка).

За графіком (рис. 3.1) знаходимо для частинок кристалічної будови Lу = 3,110².

Швидкість осадження за формулою (3.5а):

Приклад 3.4. Визначити розміри подовгастих частинок вугілля (₁ = 1400 кг/м³) і плоских частинок сланцю (₂ = 2200 кг/м³), що осідають з однаковою швидкістю _ос = 0,1 м/с у воді за температури 20 °C.

Розв’язання. Розміри частинок d_e необхідно розрахувати за рівнянням (3.7):

,

заздалегідь визначаючи значення критерію Аr за критерієм Lу з графіка (рис. 3.1) для частинок відповідної форми. Для частинок подовгастої форми:

,

де _с = 110^-3 Пас (табл. 2 додатка); _с = 1000 кг/м³.

Для частинок пластинчастої форми:

.

Значенню Lу₁ = 255 відповідає Аr₁ = 910⁴ для подовгастих частинок. Значенню Lу₂ = 85 відповідає Аr₂ = 710⁴ для частинок пластинчастої форми.

Еквівалентний діаметр частинок вугілля:

мм.

Еквівалентний діаметр частинок сланцю:

мм.

Приклад 3.5. Яку висоту треба надати шару газу між полицями пилової камери (рис. 3.9), щоб осіли частинки колчеданового пилу з діаметром 8 мкм за витрати пічного газу 0,6 м³/с (за нормальних умов)? Довжина камери – 4,1 м, ширина – 2,8 м, загальна висота – 4,2 м. Середня температура газу в камері – 427 °С. В’язкість газу за цієї температури – 0,03410^-8 Пас, густина пилу – 4000 кг/м³, густина газу – 0,5 кг/м³.

Розв’язання. Визначаємо витрату газу за заданих умов:

м³/с.

Лінійна швидкість газу (нехтуючи товщиною полиць):

м/с.

Час перебування газу в камері:

с.

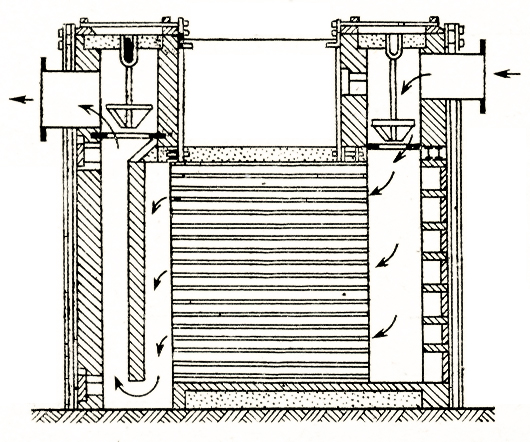
Рис. 3.6. До прикладу 3.5

Теоретична швидкість осадження кулястих частинок (величиною _с нехтуємо) за формулою (3.1):

м/с.

Дійсну швидкість осадження приймаємо такою, що дорівнює 0,5  0,0041 = 0,002 м/с.

Знаходимо відстань між полицями:

мм.

Перевіряємо правильність використання формули (3.1) :

.

Оскільки Rе = 0,00048 < 0,2, таке використання формули Стокса допустиме.

Приклад 3.6. Визначити розмір якнайменших частинок, що осідають в газоході квадратного перетину завдовжки 16 м і заввишки 2 м за лінійної швидкості газу 0,5 м/с. В’язкість газу – 0,0310^-3 Паc, густина газу – 0,8 кг/м³, густина частинок – 4000 кг/м³.

Розв’язання. Газ проходить каналом протягом:

 =16/0,5 = 32 с.

За цей час встигнуть повністю осісти тільки ті частинки, дійсна швид­кість осадження яких не менша, ніж:

_ос = 2/32 = 0,062 м/с.

Визначимо діаметр кулястих частинок, теоретична швидкість осадження яких удвічі більша, тобто дорівнює 0,124 м/с. Обчислимо значення критерію Lу за формулою (3.4а):

.

За графіком (рис. 3.1) знаходимо значення Rе = 0,14, звідки:

мкм.

Приклад 3.7. Визначити діаметр відстійника (див. рис. 3.2) для безперерв­ного осадження крейди у воді. Продуктивність відстійника – 80 т/год почат­кової суспензії, що містить 8 % (мас.) СаСО₃. Діаметр найменших частинок, що підлягають осадженню – 35 мкм. Температура суспензії – 15 °С. Вологість шламу – 70 %. Густина крейди – 2710 кг/м³.

Розв’язання. Щоб визначити діаметр відстійника, треба обчислити необхідну площу осадження за формулою (3.9), для чого заздалегідь знаходять швидкість осадження:

м/с,

де _с = 1,1410^-3 Пас (табл. 2, додатка).

Перевіримо значення критерію Rе:

 0,2.

Дійсна швидкість осадження:

м/с.

Площа відстійника:

м².

Діаметр відстійника:

м.

Приклад 3.8. Визначити висоту відстійника (див. рис. 3.2), якщо відомо, що для ущільнення суспензії в зоні згущування необхідно 16 год. Відносна гус­тина твердої фази – 2,6. Середнє розбавлення в зоні згущування – Т : Р = 1 : 1,5. Діаметр відстійника – 10 м. Добова продуктивність відстійника – 24,2 т твердої фази. Рідка фаза – вода.

Розв’язання. Знаходимо відносну густину суспензії в зоні згущування за формулою (3.26), розділивши її на :

,

де п = Р  Т = 1,5.

Масова концентрація суспензії в зоні згущування:

кг тв.фази / кг суспензії.

Отже, 1 м³ згущеної суспензії містить твердої фази:

Т = 1320  0,4 = 530 кг.

За умовою задачі, протягом доби на 1 м² осідає твердої фази:

т/м² на добу.

Отже, в зоні згущування за 16 год пройде 0,308  (16/24) = 0,205 т твердої фази на 1 м² площі осадження.

Вище знайдено, що суспензія в зоні згущування містить 0,530 т твердої фази на 1 м³; тому висота цієї зони:

h₂ = 0,205/0,530 = 0,387 м.

Висоту зони живлення приймаємо 0,45–0,75 м. Для розбавленої суспензії (Т : Р = 1 : 10) можна прийняти її такою, що дорівнює h₁ = 0,6 м.

Висота зони відстійника, в якій обертаються гребки, залежить від нахилу лопаті до дна відстійника. Приймемо її такою, що дорівнює 0,146 м на 1 м радіуса відстійника. Отже,

h₃ = 0,146  5 = 0,73 м.

Тоді загальна висота відстійника:

м  1,72 м.

Приклад 3.9. Розрахувати циклон для виділення частинок сухого матеріа­лу з повітря, що виходить із розпилювальної сушарки, за такими даними: най­менший розмір частинок – 80 мкм, витрата повітря – 2000 кг/год, температура – 100 °С.

Розв’язання. Для уловлювання частинок матеріалу розміром 80 мкм вибираємо циклон типу ДН–15.

Приймаючи р/_г = 740, діаметр циклона знайдемо за формулою:

,

заздалегідь визначаючи умовну швидкість газу в циліндричній частині циклона _ц з рівняння:

,

де ₀ = 160:

м/с.

Густина повітря: _г = 1,293·(273/373) = 0,95 кг/м³. Отже,

м.

Приймаємо діаметр циклона таким, що дорівнює 0,5 м.

Гідравлічний опір циклона:

Па або 72 мм вод. ст.

Фільтрування

Приклад 3.10. Вивести формулу (3.16), що визначає залежність між масою сухого осаду на 1 м³ фільтрату, густиною фільтрату, концентрацією суспензії та вологістю осаду.

Розв’язання. Рівняння матеріального балансу фільтрування:

,

де G_cусп, G_ф і G_вол.ос – маса суспензії, фільтрату і вологого осаду, відповідно.

Розділимо це рівняння на G_сух – масу сухої речовини, що міститься в суспензії:

. (3.48)

Масу фільтрату замінимо добутком об’єму фільтрату і його густини:

.

Введемо позначення:

, кг/кг; , кг/кг; , кг/м³.

Тоді попереднє рівняння (3.48) можна переписати так:

,

звідки

.

Приклад 3.11. Визначити тривалість фільтрування 10 дм³ рідини через 1 м² фільтру, якщо під час попереднього випробування фільтра з 1 м² було зібрано фільтрату: 1 дм³ через 2,25 хв і 3 дм³ через 14,5 хв після початку фільтрування.

Розв’язання. Згідно з дослідними даними знаходимо експериментальні константи К і С у рівнянні фільтрування:

.

Для цього додаємо два рівняння з двома невідомими:

; ,

звідки К = 0,77 дм⁶/(м⁴хв.) і С = 0,37 дм³/м².

Для визначення шуканої тривалості фільтрування отримані значення констант і заданий об’єм фільтрату підставляємо в рівняння фільтрування:

,

звідки  = 140 хв або 2 год 20 хв.

Приклад 3.12. В умовах попереднього прикладу визначити тривалість промивання осаду, якщо кількість промивної води становить 2,4 дм³/м² і промивання відбувається основним фільтром.

Розв’язання. Нехтуючи відмінністю у динамічних коефіцієнтах в’язкості фільтрату і промивної води, вважатимемо, що швидкість промивання дорівнює швидкості фільтрування в кінцевий момент.

Швидкість фільтрування в кінцевий момент визначимо за рівнянням (3.14) з використанням даних попереднього прикладу:

дм³/(м²хв).

Тривалість промивання:

хв.

Приклад 3.13. Під час дослідного фільтрування водної суспензії з вмістом 13,9 % карбонату кальцію за 20 °С на лабораторному фільтрпресі F = 0,1 м² і з товщиною осаду 50 мм отримали дані, наведені в табл. 3.2.

Визначити константи фільтрування: К (у м²/год) і С (у м³/м²).

Розв’язання. Числові значення констант фільтрування знайдемо з рівняння (3.13):

.

Таблиця 3.2

За надлишкового тиску		Зібрано фільтрату	Час від початку досліду
Па	кгс/см2	дм3	с
3,43104 10,3104	0,35 1,05	2,92 7,80 2,45 9,80	146 888 50 660

За надлишкового тиску 3,4310⁴ Па (0,35 кгс/см³) результати дослідів:

м³/м²; год.

м³/м²; год.

Підставляємо перераховані величини в рівняння (3.13) і розв’язуємо систему рівнянь:

,

,

звідки К = 27810^-4 м³/год; С = 4,710^-3 м³/м².

Аналогічно обчислюємо константи К і С для надлишкового тиску 10,310⁴ Па (1,05 кгс/см²). Отримуємо такі значення констант фільтрування: К = 56010^-4 м³/год; С = 3,7810^-3 м³/м².

Приклад 3.14. В умовах попереднього прикладу розрахувати питомий опір осаду карбонату кальцію. Додатково відомо, що вологість осаду за р₁ = 3,4310⁴ Па (0,35 кгс/см²) дорівнювала 37 %, а за р₂ = 10,310⁴ Па (1,05 кгс/см²) – 32 % від маси вологого осаду.

Розв’язання. Питомий опір осаду розраховуємо за формулою (3.18).

Тиск фільтрування: р = р₁ = 3,4310⁴ Па.

Густина фільтрату:  = 1000 кг/м³.

Динамічний коефіцієнт в’язкості фільтрату за 20 °С:

, кг/(мгод).

Константа фільтрування (за тиску р₁ = 3,4310⁴ Па) К = 27810^-4 м²/год.

Масова частка твердої фази в суспензії: х = 0,139.

Масове відношення вологого осаду до сухого – m = 1/(1 – 0,37) = 1,59.

Кількість фільтрату на 1 кг суспензії: 1 – m  x = 1 – 1,59 – 0,139 = 0,779.

Знайдені величини підставляємо у формулу (3.18):

м / кг сухого осаду.

За тиску фільтрування 10,310⁴ Па, тобто 1,05 кгс/см², маємо:

, м²/год; ; .

Інші величини мають ті самі значення, що і за р₁ = 3,4310⁴ Па, тобто 0,35 кгс/см².

Новий питомий опір осаду можна знайти підставлянням числових зна­чень цих величин у формулу (3.18) або із співвідношення:

,

звідки:

м / кг сухого осаду.

Отже, у разі збільшення тиску фільтрування утричі питомий опір осаду карбонату кальцію збільшився лише на 52%.

Приклад 3.15. Чому дорівнює питомий опір тканини під час фільтрування суспензії карбонату кальцію в умовах прикладів 3.14 і 3.15?

Розв’язання. Питомий опір тканини (у м/м²) обчислюємо за формулою (3.21)

.

За р₁ = 3,4310⁴ Па, тобто 0,35 кгс/см²:

м/м².

За р₂ = 10,310⁴ Па, тобто 1,05 кгс/см²:

м/м².

У разі зміни тиску утричі питомий опір тканини змінився лише на 19 %.

Приклад 3.16. Необхідно відфільтрувати суспензію на рамному фільтр­пресі і за 3 год отримати 6 м³ фільтрату. Дослідне фільтрування цієї суспензії на лабораторному фільтрпресі за цього самого тиску і цієї самої товщини шару осаду засвідчило, що константи фільтрування, віднесені до 1 м² площі фільтра, мають такі значення: К = 20,710^–4 м²/год і С = 1,4510^-3 м³/м². Визначити необхідні розміри фільтрпресу.

Розв’язання. Знаходимо за рівнянням фільтрування (3.13) продуктивність 1 м² фільтрпресу:

,

звідки

за цикл фільтрування, тобто за 3 год.

Отже, для заданої продуктивності необхідна поверхня фільтрування:

м².

За каталогом вибираємо найближчий більший фільтрпрес із F = 83 м², із 42 рамами розміром 1000 x 1000 мм.

Примітка. Поверхню фільтрування можна визначити також безпосередньо з рівняння (3.13), складеного для всього фільтра з поверхнею F і продуктивністю V_F, м³ фільтрату за цикл фільтрування.

; ,

звідки F = 77,4 м².

Приклад 3.17. На барабанний вакуум-фільтр безперервної дії (рис. 3.7) пода­ється 8,5 м³/год водної суспензії, що містить 17,6 % твердої фази. Бажана кінцева вологість осаду – 34 %. Передбачуваний вакуум на заводі – 600 мм. рт. ст. Під час дослідного фільтрування на лабораторній моделі за вакууму 510 мм. рт. ст. було встановлено, що необхідна вологість осаду досягається за 32 с роботи зони фільтрування. Константи фільтрування, віднесені до 1 м², виявилися такими, що дорівнюють: К = 11,2 дм⁶/(м⁴с) і С = 6 дм³/м³. Густина суспензії – 1120 кг/м³. Визначити необхідну поверхню фільтра і частоту його обертання.

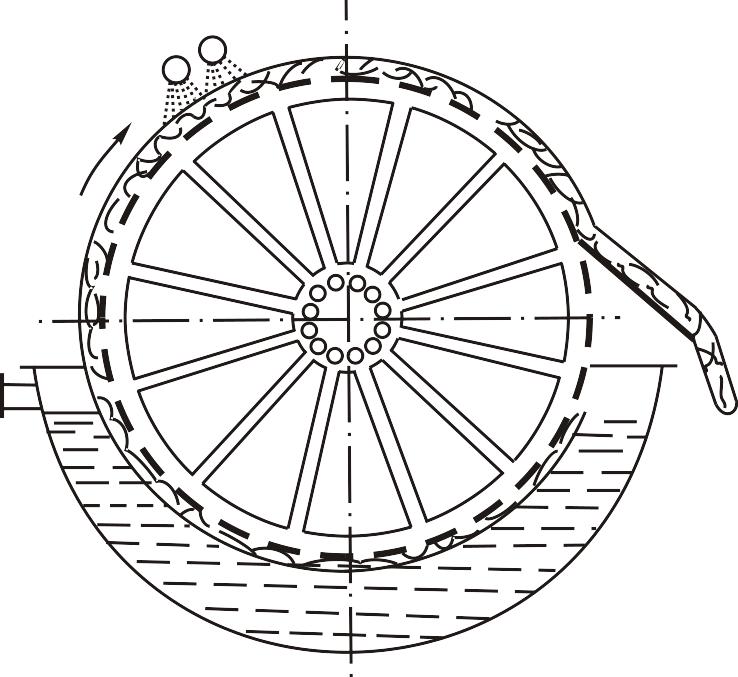
Рис. 3.7. До прикладу 3.17

Розв’язання. Перерахуємо константу фільтрування К для вакууму 600 мм. рт. ст., приймаючи приблизно, що К пропорційне до р:

К/К' = 600/510= 1,17,

звідки:

K = 11,2  1,17 = 13,1 дм⁶/(м⁴с).

Визначаємо питому продуктивність зони фільтрування з рівняння (3.13), приймаючи час фільтрування  = 32 с (за завданням):

; ;

дм³/м² за 32 с.

Отже, питома продуктивність зони фільтрування за 1 с:

15,4/32 = 0,482 дм³/(м²с).

Перераховуємо задану продуктивність за суспензією на продуктивність за фільтратом.

За вологості осаду 34 % масове співвідношення вологого і сухого осаду: т = 1/(1 – 0,34) = 1,52.

Масова частка твердої фази в суспензії: х = 0,176; витрата суспензії: G_с = V_с  _с = 8,5  1120 = 9500 кг/год; маса вологого осаду: G_ос = G_схт = = 9500  0,176  1,52 = 2540 кг/год; маса фільтрату: G_ф = G_с – G_ос = 9500 – – 2540 = 6960 кг/год.

За густини фільтрату  = 1000 кг/м³ об’ємна його витрата становить 6960 дм³/год.

Отже, задана продуктивність за фільтратом:

6960/3600 = 1,93 дм³/с.

Отже, необхідна поверхня в зоні фільтрування:

F_ф = 1,93/0,482 = 4,0 м².

Оскільки зазвичай у барабанних вакуум-фільтрах поверхня зони фільтру­вання становить ~35% від загальної поверхні, то загальна поверхня фільтра:

F = 4,0/0,35 = 11,43 м².

За каталогом підбираємо найближчий тип барабанного вакуум-фільтра з F = 12 м². Діаметр фільтра D = 2,1 м, довжина фільтра L = 1,8 м.

Частота обертання фільтра за 1 хв, необхідна для забезпечення заданого часу фільтрування  = 32 с, визначиться з пропорції:

32 – 0,35

60 – n

звідки:

n = 60  0,35/32 = 0,655 об/хв.

Приклад 3.18. Скільки часу необхідно відмивати осад на фільтрпресі від NаСl, щоб досягти концентрації 5 г/дм³, допустимої у промивній воді? Проми­вають чистою водою. Інтенсивність промивання – 0,33 м³/(м²год). Товщина шару осаду – 35 мм. Константа промивання – К = 520 см³/дм³. У початковий момент промивання концентрація NаСl у промивній воді – 143 г/дм³.

Розв’язання. Скористаємося рівнянням (3.23), підставимо в нього задані величини у відповідних одиницях вимірювання:  = 0,035 м;  = 0,33 м³/(м²год); К = 520  0,001 м³/м³.

.

Тоді:

год = 41 хв.

Приклад 3.19. В умовах попереднього прикладу розрахувати концентра­цію NаСl у промивній воді через 50 хв після початку основного періоду промивання.

Розв’язання. Концентрацію солі в промивній воді знайдемо за формулою (3.22):

.

Логарифмуючи цей вираз, одержуємо:

.

Отже, С₂ = 2,53 г/дм³.

Центрифугування

Приклад 3.20. Визначити технологічний тип і обрати конструкцію цент­рифуги для відділення поташу від маточного розчину, враховуючи те, що кон­центрація твердої речовини в суспензії становить 75 %; для осаду (криста­лічного) необхідна залишкова вологість 3 %; промивання здійснюється водою, вибілювання – парою; як маточний розчин, так і осад мають лужну реакцію.

Процес розділення необхідно механізувати, оскільки центрифуга повин­на забезпечити велику продуктивність.

Розв’язання. Для розділення системи рідина – тверде тіло у разі грубих суспензій придатні центрифуги технологічного типу 1-а.

Згідно із завданням, процес повинен бути механізований. Цьому завдан­ню відповідають центрифуги напівбезперервної (клас Б) і безперервної (клас В) дії. Враховуючи необхідність промивання осаду водою і вибілювання парою, вибираємо центрифуги напівбезперервної дії. Механізацію процесу можна забезпечити автоматизацією управління. До класу Б належать дві конструк­тивні групи центрифуг: горизонтальні та вертикальні. З числа центрифуг напів­безперервної дії найбільше розповсюджені горизонтальні центрифуги, тому вибираємо центрифугу горизонтального типу.

Приклад 3.21. Центрифуга періодичної дії має барабан із внутрішнім діа­метром 1200 мм, заввишки 550 мм, з товщиною стінок 10 мм і з масою 120 кг. Число отворів у стінці барабана за вертикаллю – 12, діаметр отворів – 5 мм. На барабан одягнено три сталеві обручі з перетином 15х30 мм² кожний. Матеріал барабана – сталь із тимчасовим опором на розрив 4500 кгс/см². Маса заванта­­ження – 400 кг, товщина шару – 200 мм. Знайти гранично допустиму частоту обертання центрифуги, якщо запас міцності не повинен бути меншим ніж 5.

Розв’язання. Для цієї сталі напруга на розрив допускається:

Па або 900 кгс/см².

Площа перетину стінки барабана і обручів з вирахуванням отворів:

см² = 6,2510^-3 м².

З формули (3.40) виходить, що максимально допустима відцентрова сила:

Н.

Відстань від центра ваги півкільця стінки барабана до осі обертання знаходимо за формулою (3.40 а):

м.

Відцентрова сила, що розвивається половиною барабана, згідно з рівнянням (3.28):

Н.

Відстань від центра ваги півкільця завантаження до осі обертання:

м.

Відцентрова сила, що розвивається півкільцем завантаження:

Н.

Загальна відцентрова сила:

Н.

Вище знайдено, що відцентрова сила не повинна перевищувати 1,110⁶ Н. Отже, максимально допустима частота обертання центрифуги:

об/хв = 17,8 об/с.

Приклад 3.22. Визначити годинну продуктивність (за живленням) автома­тичної осаджувальної центрифуги АОГ–800 під час її роботи на водній суспен­зії гідроксиду маґнію. Густина частинок –  = 2525 кг/м³. Температура суспен­зії – 30 °С. Найменший діаметр частинок – 3 мкм. Характеристика центрифуги: діаметр барабана – 800 мм; довжина барабана – 400 мм; діаметр борту – 570 мм; частота обертання – 1200 об/хв. Цикл роботи центрифуги становить 20 хв; з них 18 хв – подавання суспензії, 2 хв – розвантаження осаду.

Розв’язання. Продуктивність визначаємо за формулою (3.42):

.

Швидкість осадження частинок знаходимо за формулою Стокса:

м/с.

Динамічний коефіцієнт в’язкості води за 30 °С _с = 0,810^-3 Пас.

Визначаємо швидкість осадження під дією відцентрової сили:

м/с.

Перевіряємо режим осадження:

,

тобто режим ламінарний.

Далі знаходимо:

k = 18/20 = 0,9.

Продуктивність центрифуги, приймаючи  = 0,45:

Приклад 3.23. Визначити, яку продуктивність може забезпечити трубчас­та надцентрифуга СГО–150 з трилопатевою крильчаткою, що працює для освітлення мінеральної оливи. Густина оливи _с = 900 кг/м³. Динамічний коефі­цієнт в’язкості оливи за температури центрифугування 310^-3 Пас. Густина твердих частинок  = 1400 кг/м³. Діаметр частинок – 1 мкм. Технічна характе­ристика центрифуги: внутрішній діаметр барабана – 150 мм, діаметр зливного порога – 50 мм, довжина барабана – 750 мм, частота обертання – 13000 об/хв.

Розв’язання. Продуктивність визначаємо за формулою (3.43):

.

Оскільки частинки дуже малі, то режим їхнього осадження буде, ймовір­но, ламінарним. Скористаємося формулою Стокса з подальшою перевіркою режиму осадження:

м/с.

Швидкість осадження під дією відцентрової сили:

м/с.

Перевіряємо режим осадження:

.

Знайдемо корисний об’єм барабана центрифуги:

м³.

Глибина потоку в барабані:

м.

Тоді:

м³/год.

Перевіряємо режим потоку в барабані центрифуги:

;

м/с; м³/с;

м³.

Для центрифуги з трилопатевою крильчаткою:

м;

,

тобто режим ламінарний.

Приклад 3.24. Вибрати тип фільтрувального апарата для гелю кремнієвої кислоти і визначити необхідну кількість апаратів на підставі таких даних: 1) початкова концентрація твердої фази в суспензії – 4,7 %, відносна густина суспензії – 1,1; 2) добове завдання – 9 т вологого осаду; 3) осад повинен мати якнайменшу вологість, оскільки надалі надходить на сушіння (у вакуум-сушарку); 4) осад аморфний, погано фільтрується.

Таблиця 3.3

Характеристика	Відсосний фільтр	Центрифуга
Площа фільтрування, м2 Товщина шару осаду, мм Тривалість: фільтрування промивання лугом і водою загальна Профільтровано суспензії, дм3 Залишкова вологість осаду, % Вакуум, мм рт. ст.	1 60 1 год 2 год 3 год 170 85 400	0,3 30 45 хв 33 хв 1,3 год 108 78 –

Із попередніх дослідів фільтрування гелю на фільтрі (нутч-фільтрі) від­смоктування і на центрифузі отримали результати, наведені в табл. 3.3.

Барабан центрифуги мав D = 400 мм, Н = 250 мм, n = 800 об/хв.

Розв’язання.

1. Визначення тиску фільтрування.

Фільтр відсмоктування:

кгс/см² = 5,1510⁴ Па.

Центрифуга

Для коефіцієнта заповнення барабана центрифуги під час її роботи  = 0,5 об’єм суспензії (робочий об’єм барабана):

м³.

Тиск фільтрування для центрифугування визначаємо за формулою (3.29):

Отже, тиск під час центрифугування був у 1,5 разів більший, ніж під час фільтрування на фільтрі відсмоктування.

2. Визначення питомої продуктивності.

Фільтр відсмоктування

Профільтровано 170 дм³ суспензії із початковою концентрацією 4,7 %, тобто зібрано гелю, перераховуючи на суху речовину:

кг.

Тривалість усієї операції 3 год (без урахування часу на розвантаження), отже, питома продуктивність:

кг сухого гелю/(м²год).

Враховуючи вологий гель (за вологості 85 %):

2,94/0,15 = 19,5 кг вологого гелю/(м²год).

Центрифуга

Профільтровано 108 дм³ суспензії, отже, отримано осаду, перераховуючи на суху речовину:

кг.

Відповідно, питома продуктивність:

кг сухого гелю/(м²год).

Перераховуючи на вологий гель (за вологості 78 %):

14,3/0,22 = 65 кг вологого гелю/(м²год).

3. Зіставимо, наскільки більше треба видалити води під час сушіння вологого гелю після фільтра відсмоктування порівняно з гелем, відтисненим на центрифузі.

Вологість осаду на фільтрі відсмоктування становить 85 %, а на центри­фузі – 78 %, отже, центрифуга видаляє води більше, ніж фільтр відсмоктування на 2120 кг:

кг води/ кг сухого гелю.

Зіставляючи дослідні та розрахункові дані з фільтрування гелю, можемо констатувати.

Центрифуга, працюючи з тиском фільтрування у 0,83/0,525 = 1,6 разів більшим і за товщини шару осаду удвічі меншої, ніж у разі фільтра відсмок­тування, має продуктивність у 14,3/2,94  5 разів більшу, ніж фільтр відсмок­тування (перераховуючи на сухий гель; у перерахунку на вологий осад продук­тивність центрифуги більша у 65/19,5 = 3,3 разів).

Центрифуга, порівняно з фільтром відсмоктування, дає меншу залишкову вологість і тим самим полегшує роботу сушарки, звільняючи її від випарову­вання 2,12 т води (перераховуючи на 1 т сухого гелю).

За добової продуктивності 9 т гелю із вологістю 78 % і питомої витрати пари на сушіння, що дорівнює 1,5 кг/кг випаровуваної вологи, економія пари за добу становитиме:

т

Більша питома продуктивність центрифуги, менша залишкова вологість осаду і, отже, істотна економія пари під час сушіння гелю вимагають у цьому разі віддати перевагу центрифузі, незважаючи на її вищу вартість.

4. Визначимо орієнтовно кількість промислових центрифуг, необхідних для виконання добового завдання (9 т вологого гелю).

Для цього попередньо вибираємо центрифугу напівнеперервної дії з механічним вивантаженням осаду і автоматичним керуванням. За каталогом вибираємо горизонтальну центрифугу з такою характеристикою: D = 1600 мм, Н = 700 мм, n = 500 об/хв, корисний об’єм – 500 дм³.

Поверхня фільтрування цієї центрифуги:

м².

Тиск фільтрування, що розвивається, за формулою (3.29) становить:

.

Отже, промислова центрифуга розвиває тиск фільтрування у 3,5/0,83 = 4 рази більший, ніж дослідна.

Орієнтовно продуктивність фільтрів пропорційна до , отже, можна очі­кувати збільшення питомої продуктивності центрифуги майже удвічі, тобто до 65  2 = 130 кг вологого гелю/(м²год).

Оскільки фільтрування і промивання осаду займають приблизно 75 % від загального часу роботи центрифуги напівбезперервної дії, то її середня годинна продуктивність становить 130  0,75 = 97 кг/(м²год).

Отже, добова продуктивність однієї центрифуги, приймаючи для неї 20 робочих годин у добу, становитиме 973,520 = 6800 кг вологого осаду.

Для забезпечення всієї заданої добової продуктивності необхідно встано­вити 9000/6800 = 1,32, тобто дві центрифуги, а з резервом – три.

Перемішування в рідкому середовищі

Приклад 3.25. Суміш кислот (густина – 1600 кг/м³, динамічний коефіці­єнт в’язкості – 210^-2 Пас) готують в апараті без перегородок (діаметр – 1200 мм, висота – 1500 мм), заповненому на 0,75 об’єму. Початкові кислоти перемішують пропелерною мішалкою із частотою обертання 3,5 об/с (рис. 3.11). Визначити необхідну установчу потужність електродвигуна.

Розв’язання. Знаходимо діаметр нормалізованої мішалки:

d = D/3 = 1,2/3 = 0,4 м.

Визначаємо режим перемішування за формулою (3.60):

.

Режим – турбулентний.

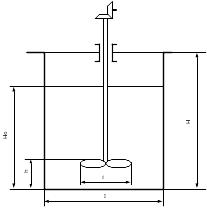
Рис. 3.8. До прикладу 3.25

Визначаємо значення критерію потужності за графіком (рис. VII) [4]: К_N = 0,27.

Розраховуємо потужність, споживану мішалкою за сталого режиму, за рівнянням (3.61):

Вт = 0,2 кВт.

Потужність у пусковий момент здебільшого у 2–3 рази перевищує робочу:

кВт.

Визначаємо встановлювану потужність, приймаючи ККД електродвигуна з передачею 0,95 і запас потужності у 20 %:

кВт.

Приклад 3.26. Електродвигун потужністю 16,5 кВт із приводом, що знижує частоту обертання до 240 об/хв, приводить у дію відкриту турбінну мішалку з шістьма лопатками; мішалка інтенсивно розмішує реакційну масу ( = 1200 кг/м³,  = 1,6 Пас) у посудині діаметром 1630 мм із перегородками. Який повинен бути діаметр мішалки?

Розв’язання. Оскільки зумовлено інтенсивне перемішування, можна вва­жати режим розвиненим турбулентним. За рис. VII [4] знаходимо: К_N = 6,9.

За формулою (3.61):

м.

Перевіримо відношення D/d:

D/d=1,63/0,5 = 3,26.

Приклад 3.27. У реакторі (рис. 3.9) з діаметром 3000 мм, заповненому на висоту 1000 мм реакційною масою, що має за температури перебігу процесу  = 15010^-3 Пас і _с = 1200 кг/м³, необхідно забезпечити рівномірний розподіл твердих частинок каталізатора з найбільшим розміром 1,3 мм і густиною 2450 кг/м³; Т : Р = 1 : 4.

Яку мішалку доцільно використовувати – пропелерну трилопатеву (рис. 3.10, а) із кроковим відношенням 1 або турбінну (рис. 3.10, 6) закритого типу з вісьма лопатями?

Розв’язання. 1. Визначаємо діаметр нормалізованої мішалки:

м.

2. Для знаходження необхідних значень критерію Rе_ц і величини визна­чальної частоти обертання скористаємося узагальненим рівнянням:

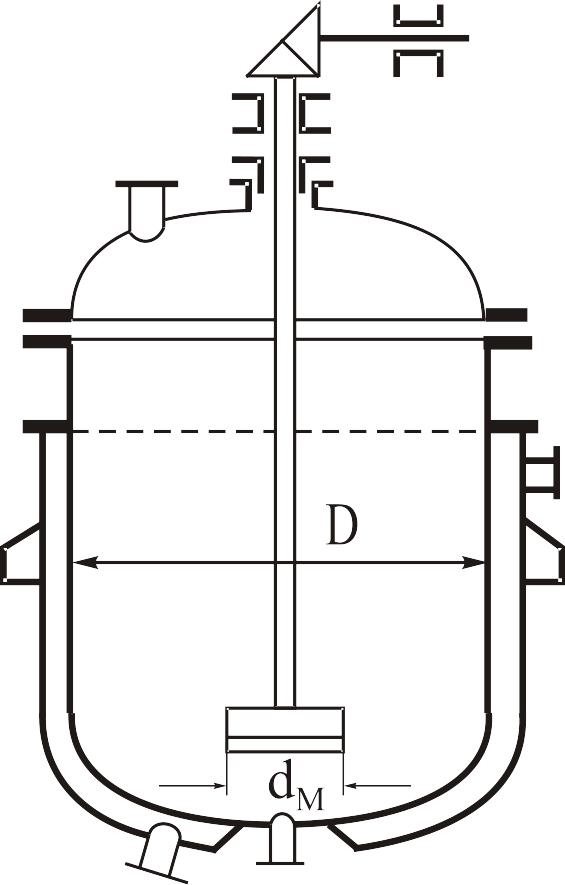
Рис. 3.9. До прикладу 3.27

У цьому рівнянні:

	C	k	l	m	n
Для пропелерної мішалки	0,105	0,6	0,8	0,4	1,9
Турбінної	0,25	0,57	0,37	0,33	1,15

Обчислюємо значення критеріїв і симплексу подібності:

.

.

.

.

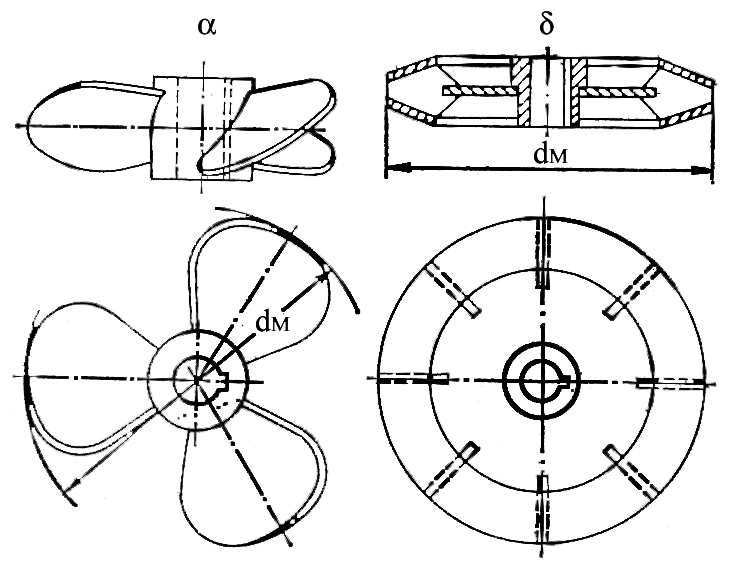
Рис. 3.10. До прикладу 3.27

Знайдені величини критеріїв і симплексу подібності знаходяться у межах застосування рівняння.

Знаходимо значення критерію Rе_ц і визначальної частоти обертання для пропелерної мішалки:

об/с = 376 об/хв.

Знаходимо значення критерію Rе_ц і визначальної частоти обертання для турбінної мішалки:

об/с = 238 об/хв.

3. Визначаємо потужність, затрачувану безпосередньо на перемішування.

З рис. VII [2] знаходимо для пропелерної мішалки: К_N = 0,32; для турбін­ної мішалки: К_N = 1,3.

Обчислюємо постійний множник:

.

Потужність, споживана пропелерною мішалкою:

Вт = 0,23 кВт.

Потужність, споживана турбінною мішалкою, становить:

Вт = 0,23 кВт.

Оскільки в цьому випадку потужність, споживана на перемішування, одна­кова, вибираємо турбінну мішалку, що працює за меншої частоти обертання.

Приклад 3.28. Досліди з окислення сульфіду амонію в тіосульфат киснем, проведені в модельному апараті діаметром 500 мм із чотирма відбивними пере­городками, засвідчили, що під час перемішування закритою турбінною мішал­кою з діаметром 125 мм, із частотою обертання 6 об/с і за питомої витрати кис­ню u_м = 3,510^-3 м³ О₂/(м³с) забезпечується поглинання 1,04 дм³ кисню на 1 м³ реакцій­ного середовища за 1 с – питома продуктивність k_м = 1,0410^-3 м³ О₂/(м³с).

На підставі результатів модельних дослідів проектується промисловий апа­рат з діаметром 2 м із мішалкою з діаметром 0,5 м, геометрично подібний до модель­ного (Г_D = D/d = 4). Необхідно розрахувати частоту обертання мішалки у промис­ловому апараті, за якої забезпечується така сама питома продуктив­ність, як і в мо­дельних умовах. Витрата кисню в промисловому апараті стано­вить u_п = 3,510^-3 м³ О₂/(м³с); фізичні властивості реакційного середовища в модельному і у промисловому апара­тах близькі до властивостей води. Темпе­ратура реакції – 80 ^оС.

Розв’язання. Для розрахунку промислових апаратів, у яких Rе_ц  1,810⁵, використовують рівняння:

, (а)

де Di = k/n – критерій Дьяконова; К_u = u/n – критерій розподілу.

Якщо під час переходу від моделі до промислового апарата властивості реагуючих фаз не змінюються, рівняння (а) зводимо до вигляду:

.

Обчислюємо значення критерію Рейнольдса (відцентрового) для модель­ного апарата:

.

Отже, результати дослідів можна використати для моделювання.

За результатами досліджень на моделі визначаємо коефіцієнт С₁ для цього процесу:

.

Підставляючи в рівняння характеристики промислового апарата і знайде­не значення С₁, розрахуємо частоту обертання мішалки:

об/с.

Приймаємо швидкість обертання мішалки n_п = 3 об/с. Перевіряємо значення критерію Рейнольдса для промислового апарата:

.

Оскільки значення критерію Рейнольдса для промислового апарата також знаходиться в межах використання рівняння (а), вибрана частота обертання забезпечить задану продуктивність.