Проінтегруємо останнє рівняння:

, (1.75)

де R – внутрішній діаметр ротора; r_o – радіус вільної поверхні рідини; τ – час осадження.

За час осадження частинка проходить найбільший шлях, що дорівнює R – r_o.

Після інтегрування:

, (1.76)

звідки:

τ = . (1.77)

Отже, час осадження залежить від радіуса барабана і вільної поверхні рідини, частоти обертання барабана, розмірів частинок і фізичних властивостей твердої та рідкої фаз (які визначають швидкість осадження у полі сил тяжіння).

Розділювальна здатність відстійних центрифуг характеризується індек­сом продуктивності Σ, який визначають добутком площі циліндричної поверхні осадження S в роторі та чинника розділення F_r:

Σ = S  F_r. (1.78)

Індекс продуктивності являє собою поверхню відстійника, в якому для цієї суспензії досягається така сама продуктивність, що і в центрифузі, яку розглядають. Величина Σ відображає вплив конструктивних особливостей центрифуги на її роздільну здатність.

Розглянемо вираз для індексу продуктивності стосовно центрифуги, зображеної на рис. 1.28. Товщина шару рідини h на практиці є значно меншою від діаметра D, тому величину чинника розділення можна зарахувати до середнього діаметра (D – h). Тоді відповідно до виразу (1.71):

. (1.79)

Площа циліндричної поверхні осадження в роторі:

Звідси:

. (1.80)

Якщо прийняти, що рідина в роторі переміщається не усім кільцевим простором, який займає шар, а тільки його тонкою внутрішньою зоною (поверхневий режим течії), то наближено:

і S = 2  π  r_o  L.

У цьому випадку:

. (1.81)

Рівняння (1.81) можна використовувати за умови, якщо осадження твер­дих частинок суспензії здійснюється за ламінарного режиму. Однак через значну величину відцентрової сили, осадження частинок у центрифугах може відбуватись в умовах перехідного та турбулентного режимів. У цих випадках індекс продуктивності визначають так:

– для перехідного режиму:

Σ = S  F_r^0,715; (1.82)

– для турбулентного режиму:

Σ = S  F_r^0,5. (1.83)

З рівнянь (1.82) і (1.83) очевидно, що в цих випадках площа відстійника, еквівалентного за продуктивністю до центрифуги, яку розглядають, зростає не пропорційно до чинника розділення, а менш інтенсивно.

1.5.3. Процеси у фільтрувальних центрифугах

Рушійною силою розділення у фільтрувальних центрифугах, так само як і у відстійних, є відцентрова сила. Розглянемо фільтрування у відцентровому полі. Ротор центрифуги з радіусом R (рис. 1.29) заповнений рідиною, яка оберта­ється разом із ротором з постійною кутовою швидкістю ω. Внутрішній радіус кільця рідини позначимо через r₁. Визначимо відцентрову силу dF_в для елементарного кільця з масою dm, радіусом r, товщиною dr і шириною ΔL, що дорівнює одиниці:

dF_в =  . (1.84)

Підставимо в отримане диференціальне рівняння значення dm = ρ  2  π  r  dr і визначимо тиск Р_в, який виникає від дії відцентрового поля:

, (1.85)

де dS = 2  π  r – поверхня елементарного кільця рідини з радіусом r.

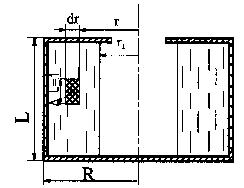
Рис. 1.29. Схема відцентрового фільтрування

Після інтегрування (1.85) у межах від r₁ до R отримаємо:

^. (1.86)

Варто зауважити, що на відміну від звичайного фільтрування, відцент­рове фільтрування відбувається в складніших умовах: осад і фільтрувальна перегородка мають значну кривизну, внаслідок чого фактична поверхня фільтрування змінюється вздовж радіуса, під час фільтрування відбувається осадження твердої фази суспензії, осад ущільнюється як під дією гідростатич­ного тиску рідини, яка обертається, так і масових сил самого осаду.

У фільтрувальних центрифугах здебільшого розділюють достатньо концент­ровані та грубодисперсні суспензії, тому можна припустити, що процес відцентро­вого фільтрування здійснюється за законом фільтрування з утво­ренням осаду.

Підставимо в рівняння фільтрування (1.35) величину відцентрового пере­паду тисків і отримаємо з урахуванням (1.38) основне рівняння відцентрового фільтрування:

(1.87)

або після нескладних перетворень з урахуванням схеми на рис. 1.28:

, (1.88)

де r_c і V_з – середній радіус і об’єм кільця завантаження.

Рівняння (1.87) або (1.88) має назву основного рівняння відцентрового фільтрування.

Розв’язок рівняння (1.87) залежить від умов проведення процесу, який можна здійснювати в таких режимах:

– за сталої різниці тисків;

– за сталої швидкості фільтрування;

– за сталих різниці тисків і швидкості фільтрування;

– за заданої зміни витрати суспензії;

– за сталої витрати суспензії.

Розглянемо, як приклад, режим за сталої різниці тисків. У цьому режимі розрізняють три стадії: поступове заповнення ротора суспензією до певної межі, коли процес відбувається за сталої витрати суспензії (перша стадія). Потім процес продовжується за сталої різниці тисків (друга стадія), під час якої рівень суспензії у роторі підтримується незмінним. Після утворення шару осаду певної товщини подавання суспензії припиняють і починається третя стадія (за змінної різниці тисків та швидкості фільтрування), яка закінчується, коли рівень рідини досягає внутрішньої поверхні шару осаду, тобто коли починається віджимання осаду. У промисловості завантаження ротора нама­гаються провести якнайшвидше, а подавання суспензії припи­няють, коли товщина шару рідини над осадом досягає мінімальної величини, тому сумарний час першої та третьої стадій, здебільшого, не перевищує 15–20 % від загального часу всього періоду фільтрування, внаслідок чого процес відбувається переважно за сталої різниці тисків.

З рівняння (1.86) очевидно, що сталий статичний тиск рідини під час її обертання можна забезпечити тільки, якщо підтримувати сталим рівень (r_o = const), тобто сталий об’єм завантаження. Тому під час відцентрового фільтрування в режимі сталої різниці тисків об’єм суспензії, який надходить у ротор за одиницю часу, повинен дорівнювати об’єму отриманого за цей час фільтрату. Приймаємо, що за час першої стадії (заповнення ротора до об’єму V_з) отриманий питомий об’єм фільтрату V₁, а на перегородці утворився шар осаду h_o = V₁  x_o (x_o – відношення об’єму осаду до об’єму фільтрату). Тоді ос­новне рівняння відцентрового фільтрування набуває вигляду:

, (1.89)

де – об’єм фільтрату у стадії фільтрування.

Після розділення змінних, інтегрування і нескладних перетворень отри­маємо залежність між об’ємом фільтрату і часом фільтрування:

. (1.90)