Глава II. Корреляционно-регрессионный анализ и его применение.

Важной задачей обработки геофизических данных является изучение зависимостей между физическими свойствами и атрибутами. Например, между различными физическими свойствами горных пород, между показаниями различных методов, между разными статистическими атрибутами. Другой распространенной задачей обработки является сглаживание, интерполяция и аппроксимация исходных или преобразованных данных. Эти задачи решаются на основе корреляционно-регрессионного анализа.

Математической моделью корреляционно-регрессионного анализа служит система случайных величин

2.1. Корреляция и регрессия.

Зависимость, при которой изменение одной случайной величины вызывает изменение распределения другой, называется статистической. При статистической зависимости различают корреляцию² для установления взаимосвязи между двумя или более случайными величинами с оценкой тесноты этой связи, и регрессию, при которой устанавливается форма (характер) зависимости между случайными величинами, чаще всего в виде полиномов.

Оценка тесноты связи производится путем расчета коэффициента ковариации , равного для двух случайных величин х и y:

(2.1)

где и - средние значения величин х и y.

Поскольку размерности х и y могут быть разные, то вычисляют коэффициент корреляции обычно в виде

(2.2)

где и - среднеквадратические отклонения Х и Y.

Коэффициент корреляции (2.2) изменяется от -1 до +1. При корреляция положительна, при корреляция отсутствует, при говорят о наличии обратной корреляции между двумя случайными величинами.

В общем случае, когда число значений и различно, коэффициент корреляции вычисляется по формуле:

где - число значений, принимающих одновременно величины и , n – общее число и .

В том случае, когда число случайных величин больше двух (N>2), корреляция оценивается либо по ковариационной матрице B, равной:

(2.3)

где - коэффициенты ковариации, причем , а по диагонали матрицы (2.3) расположены дисперсии случайных величин , либо по корреляционной матрице R, равной

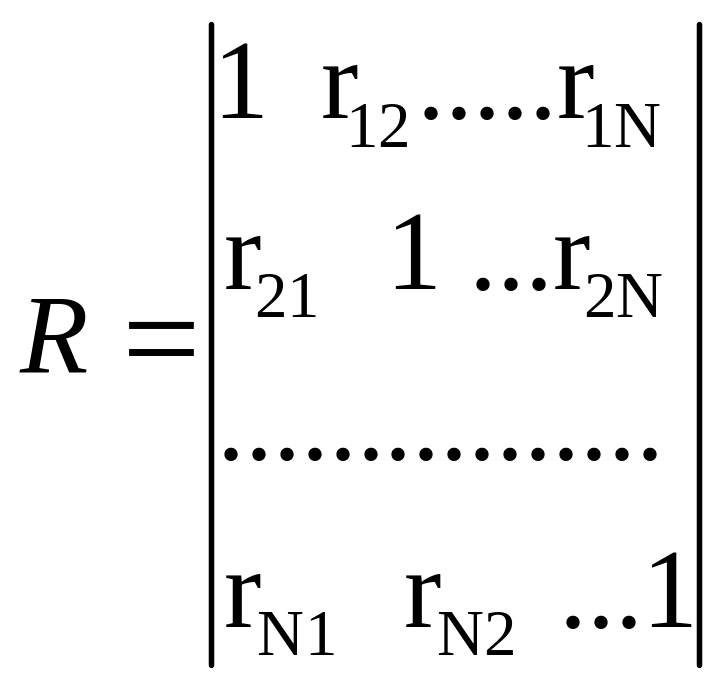(2.4)

где - коэффициенты корреляции, . Обе матрицы (2.3) и (2.4) симметричны относительно главной диагонали.

Под регрессией понимают сглаживание экспериментальной зависимости по методу наименьших квадратов. Метод наименьших квадратов состоит в минимизации суммы квадратов отклонений сглаживающей прямой (кривой) от экспериментальной зависимости , т.е.

где может быть линейная , нелинейная или множественная регрессия.

Метод наименьших квадратов приводит к системе нормальных уравнений для нахождения коэффициентов регрессии

Эта система уравнений в матричной форме выражается следующим образом

(2.5)

где X - матрица значений исходных случайных величин ; - транспонированная к X матрица; А – матрица-столбец коэффициентов регрессии ; Y – матрица-столбец случайной величины Y, для которой устанавливается форма (вид) регрессии, обычно в виде полинома.

На базе регрессионного анализа решаются две основные задачи: а) установление формы корреляционной связи, т.е. вида регрессии; б) оценка тесноты корреляционной связи. Ниже рассматриваются различные виды регрессий путем решения системы уравнений (2.5).