5.2. Спектры непрерывных сигналов.

Вначале рассмотрим спектры непрерывного периодического сигнала с периодом Т. Для нахождения коэффициентов Фурье и для такого сигнала следует задать предельные соотношения , т.е. ; ; .

При этом выражения (5.3) принимают вид:

; ,

или

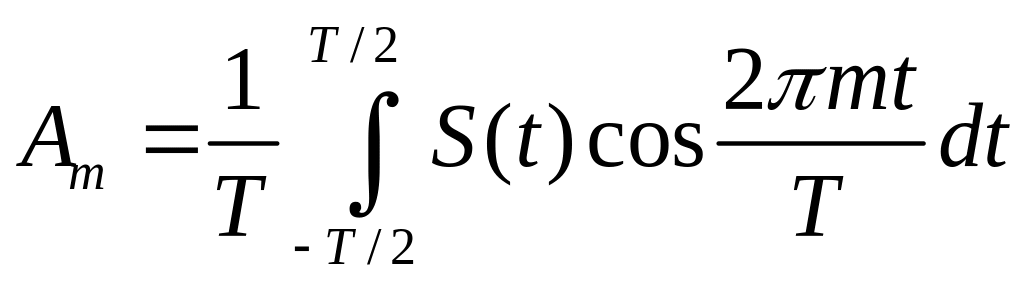; (5.10)

Формулы для амплитудного (5.4) и фазового (5.5) спектров непрерывного периодического сигнала остаются прежними, их характер также линейчатый, однако ввиду того, что стремится к бесконечности, то число гармоник бесконечно. Комплексный спектр:

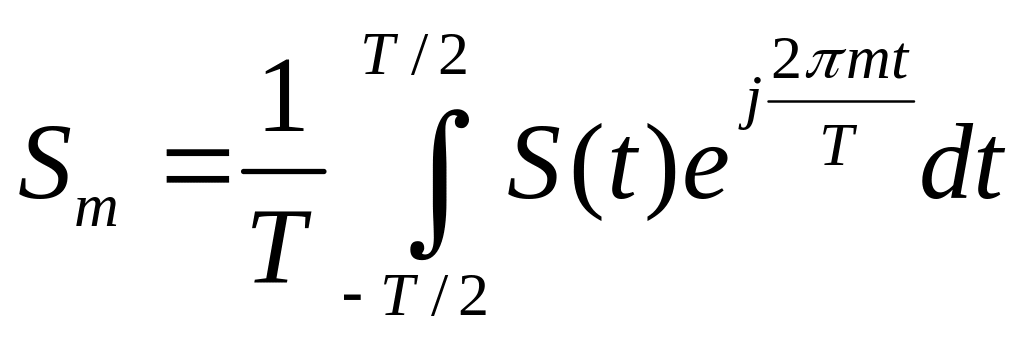(5.11).

Соответственно, обратное преобразование Фурье: .

Средняя мощность сигнала, или его дисперсия, будет

.

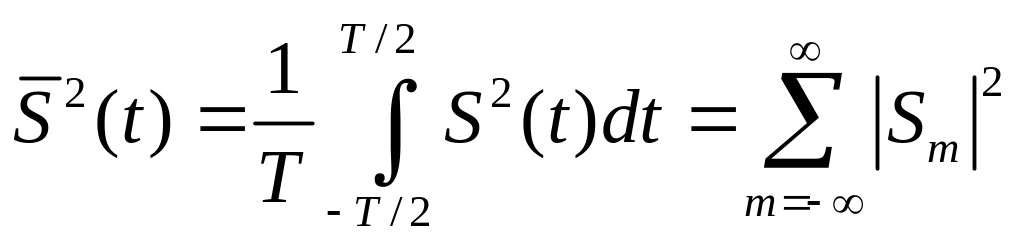В качестве примера рассмотрим расчет спектра непрерывного сигнала прямоугольной формы с единичной амплитудой длительностью и с периодом . Этот сигнал соответствует операции осреднения поля в окне размером .

Коэффициенты Фурье такого сигнала равны

= ;

.

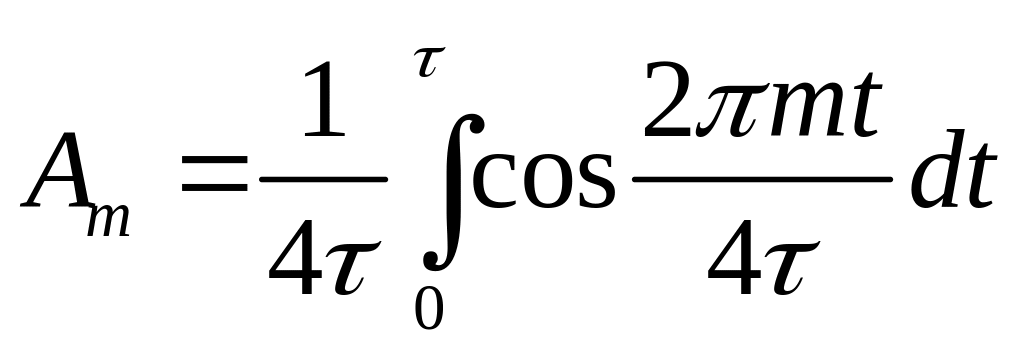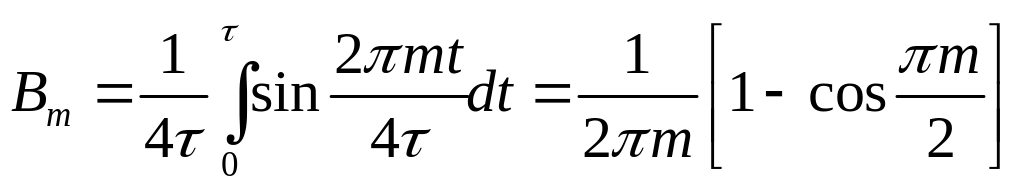Соответственно, амплитудный спектр будет

Фазовый спектр

.

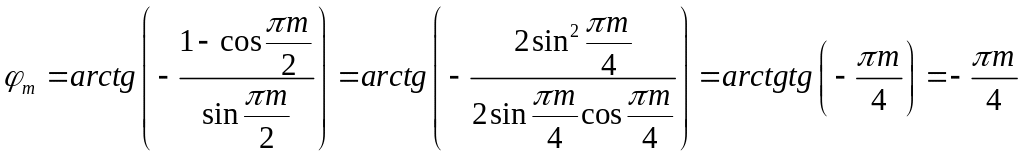Перейдем к рассмотрению спектров непрерывного апериодического сигнала, т.е. когда .

При этом коэффициенты Фурье (5.10) с учетом того, что ; , принимают вид:

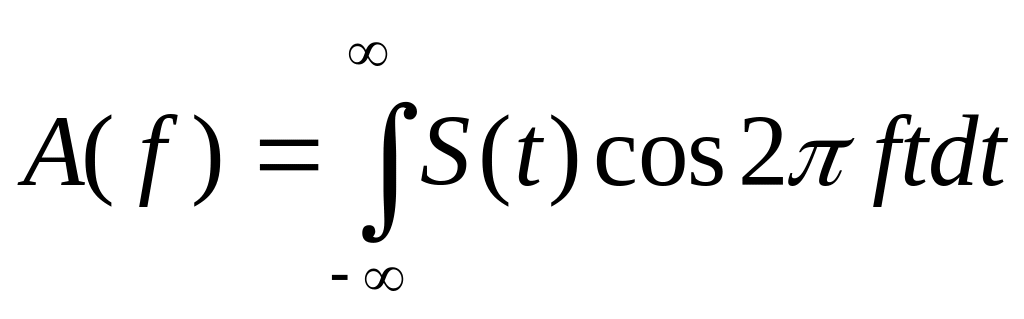; (5.12)

Комплексный спектр

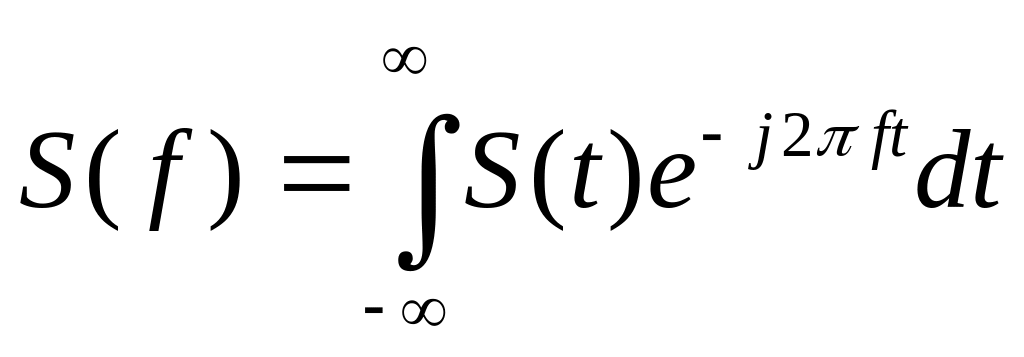(5.13)

Обратное преобразование Фурье:

(5.14)

Если ввести круговую частоту и выражение (5.14) умножить и разделить на , то получим из (5.13) и (5.14) пару преобразований Фурье:

(5.15)

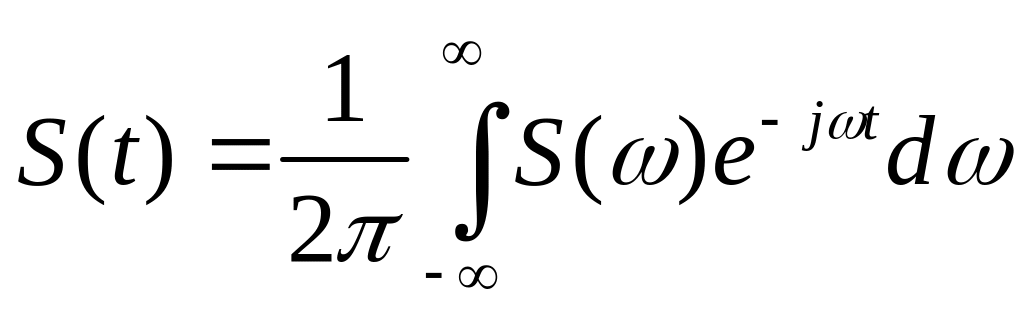
5.3. Спектры стационарного случайного процесса.

Стационарный случайный процесс полностью описывается его автокорреляционной функцией, поэтому спектр случайного процесса определяется спектром АКФ. Спектр АКФ показывает, какого рода колебания (гармоники) преобладают в случайном процессе и какова его внутренняя структура. Отличие от спектров детерминированных сигналов состоит в том, что для случайного процесса амплитуды гармоник являются случайными величинами, а сам спектр случайного процесса описывает распределение дисперсий по различным гармоникам (частотам). К вычислению спектра случайного процесса можно подходить в зависимости от того, каким образом задана АКФ: в виде дискретно заданного сигнала, непрерывного периодического или непрерывного апериодического сигналов.

Поскольку АКФ – четная функция, то при анализе Фурье учитываются лишь четные (косинусные) гармоники. В зависимости от способа задания АКФ получаем спектры для АКФ в виде дискретно заданного сигнала :

для АКФ в виде непрерывного периодического сигнала :

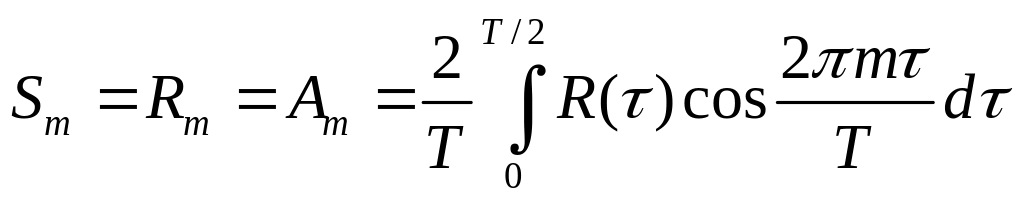
Для АКФ в виде непрерывного апериодического сигнала :

(5.16).

Поскольку нечетные гармоники для спектра АКФ отсутствуют, то приведенные выражения совпадают с энергетическими спектрами. Очевидно, что обратное преобразование Фурье для АКФ симметрично прямому. Так, для (5.16) получаем: 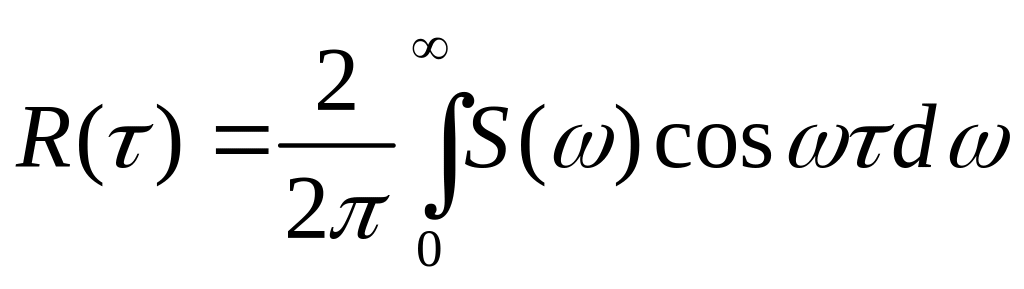(5.17).

Выражение (5.16) используется для расчета спектров наиболее распространенных АКФ в аналитическом виде:

1) АКФ «белого» шума, заданной в виде дельта-функции, т.е.

Спектр АКФ

2) АКФ «треугольного» типа ; .

3) АКФ «марковского» типа ; ;

4) АКФ «гауссовского» типа ; ;

5) АКФ затухающей по экспоненте косинусоиды .

.

АКФ гауссовского типа представляет модель гравитационных аномалий, АКФ затухающей по экспоненте косинусоиды – модель сейсмического импульса ( - определяет затухание;  - видимый период.