1.1 Определение вероятности попадания случайной величины х с использованием приведенной табличной функции распределения

Приведенная табличная функция распределения имеет вид (Таблица 1 Приложения к Практикуму):

,

где

В основу определения вероятности попадания случайной величины Х на интервал от х₁ до х₂ с использованием табличной функции распределения положено, что (рисунок 3)

F(x)

1

0,5

х

Рисунок 3

Выражение для определения вероятности с использованием приведенной табличной функции распределения имеет вид:

Подставив значения в выражение для определения вероятности попадания на интервал(х₁ х₂) получим:

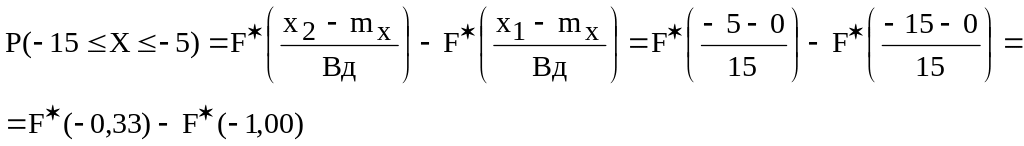
Значение функции распределения по известному аргументу определим из Таблицы 1 Приложения к Практикуму:

;

Таким образом, искомая вероятность будет равна:

1.2 Определение вероятности попадания случайной величины на заданный интервал с использованием табличной функции плотности распределения

Приведенная табличная функция плотности распределения имеет вид (Таблица 2 Приложения к Практикуму)

,

где .

Решение данной задачи с использованием табличной функции плотности распределения предполагает вычисление площади прямоугольника с высотой и основанием (рисунок 4):

х

х_ср

Рисунок 4

Выражения для определения вероятности с использованием приведенной табличной плотности распределения имеет вид:

,

где .

Несколько видоизменим условие задачи.

Выберем за начало координат ближнюю границу цели, тогда (рисунок 5). Таким образом задача сведётся к определению вероятности попадания случайной величины Х на интервал от 0 до 10 т.е. Р(0 < X < 10).

0

10

15

х

х₁

х₂

m_x

Рисунок 5

Решение:

Найдём и, подставив значения в выражение для определения вероятности, получим:

.

Зная, что функция плотности распределения четная , то:

Значения функции плотности и распределения по известному аргументу определим по Таблице 2 Приложения к Практикуму:

.

Таким образом, искомая вероятность будет равна:

.

Следует отметить, что достаточную сходимость результатов решение задачи по вычислению вероятности с использованием табличной функции плотности распределения возможно получить при выполнении условия:

1.3 Определение вероятности попадания случайной величины на заданный интервал с использованием таблиц приведенной функции Лапласа

Приведенная функция Лапласа имеет вид:

,

где .

Вероятность попадания случайной величины на заданный интервал с использованием приведенной функции Лапласа определяется из выражения:

Решение.

Опять видоизменим условия задачи, выбрав за начало координат центр цели, тогда: (рисунок 6).

0

-5

5

10

х

х₁

х₂

m_x

ЦЦ

Рисунок 6

Таким образом задача сведётся к определению вероятности попадания случайной величины Х на интервал от -5 до 5, т.е. Р(-5  X  5).

Подставив значения в выражение для определения вероятности с помощью приведенной функции Лапласа, получим:

Так как функция Лапласа нечётная , то

Значения приведенной функции Лапласа по известному аргументу определим из Таблицы 3 Приложения к Практикуму:

, .

Таким образом, искомая вероятность будет равна:

Рассчитанные значения вероятностей попадания случайной величины на заданный интервал различными способами дают достаточную близость полученных результатов.

Вывод: Полученный результат означает, что при проведении достаточно большого числа стрельб в аналогичных условиях в среднем в 16 случаях из 100 будет получено попадание в полосу.

Сформулируем ряд основных свойств табличной функции Лапласа.

1. Функция Лапласа является неотрицательной функцией:

.

2. Табличная функция Лапласа есть нечётная функция:

Заключительная часть занятия:

• напомнить тему и учебные вопросы занятия;

• отметить степень достижения учебных целей;

• ответить на возникшие у студентов вопросы.

На занятии иметь:

Калькуляторы – на каждого.

Задание на самостоятельную работу

Изучить:

1. Вентцель Е.С. Теория вероятностей. Учебник. Издание восьмое, стереотипное. – М.: Высшая школа, 2002 г. - 575 с., стр. 222-227

2. Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие. Издание десятое, стереотипное. - М.: Высшая школа», 2004 г. – 480 с. стр. 116-123.

Лекция 8 Определение дискретной случайной величины и её законы распределения

Учебные и воспитательные цели:

1. Ознакомить студентов с дискретными случайными величинами и законами их распределения.

Вид занятия: лекция.

Продолжительность занятия: 90 минут.

Учебно-материальное обеспечение занятия:

Медиа-проектор, ноутбук, слайды Power Point (Оверхэд-проектор, слайды).

Литература:

а) основная:

1. Баврин И.И., Матросов В.Л. Высшая математика: Учебник для студентов высших учебных заведений. – М.: Гуманит. изд. центр ВЛАДОС, 2003 г. - 400 с.

Структура занятия и расчёт времени

Структура занятия	Время, мин
I. Вводная часть занятия	5
II. Основная часть занятия	80
Введение в лекцию	5-10
1. Понятие случайной величины	30
2. Законы распределения дискретных случайных величин	30
Заключение по лекции	5
III. Заключительная часть занятия	5