3. Формула Бернулли

Перед изложением третьего вопроса лекции преподаватель обозначает проблему, вызывающую необходимость рассмотрения теоремы о повторении опытов, при этом отмечая, что в изучаемом курсе теории вероятностей будет рассматриваться только частная теорема, связанная с повторением независимых опытов, в каждом из которых событие А появляется с постоянной вероятностью.

После чего преподаватель показывает доказательство этой теоремы (вывод формулы Бернулли).

Для пояснения физической сущности рассматриваемой теоремы преподаватель использует оверхэд-проектор и подготовленные слайды.

В заключении лекции преподаватель поясняет почему распределение вероятностей появления события А в серии из n испытаний, в условиях когда они несовместны и образуют полную группу событий называют биномиальным и обращает внимание на важность знания этого распределения для решения прикладных задач.

До сих пор мы рассматривали комбинации сравнительного небольшого числа событий, когда непосредственное применение правил сложения и умножения вероятностей не вызывало больших вычислительных затруднений. Однако с увеличением числа событий или числа испытаний, в которых может появляться интересующее нас событие, изученный способ вычисления становится очень громоздким.

При этом задача решалась достаточно просто только в том случае, если опыты являлись независимыми.

Несколько опытов называются независимыми, если вероятность того или иного исхода каждого из опытов не зависит от того, какие исходы имели другие опыты.

На практике имеют место случаи, когда вероятность наступления события А во всех независимых опытах может быть либо одинаковой, либо меняться от опыта к опыту. Например, при корректировании огня после каждого выстрела вероятность попадания в цель с каждым выстрелом будет изменяться.

В случае, когда в независимых опытах вероятность наступления события от опыта к опыту изменяется, используют общую теорему о повторении опытов, а когда в независимых опытах вероятность наступления события от опыта к опыту не изменяется, используют частную теорему о повторении опытов.

В изучаемом нами курсе теории вероятностей мы рассмотрим только частную терему о повторении опытов, когда необходимо определить вероятность наступления события А в серии из n независимых опытов, в каждом из которых событие А появляется с одинаковой вероятностью.

Например, необходимо вычислить вероятность того, что при пяти выстрелах из орудия на постоянных установках будет получено ровно два попадания в цель, если выстрелы независимы и при каждом выстреле вероятность попадания в цель известна и не изменяется.

В случае, если составить возможные комбинации появления интересующего нас события А₁, то получим:

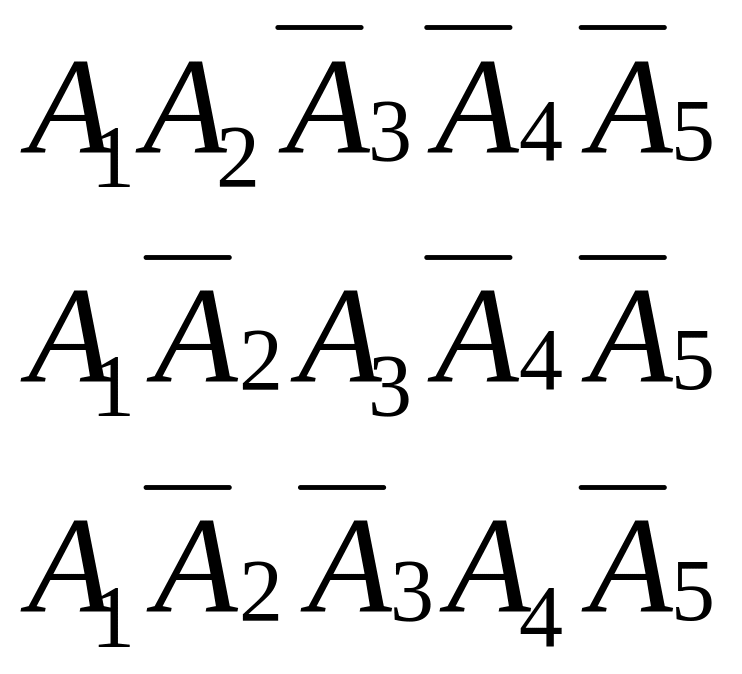
т.д.

Возможных комбинаций, в которых наступит событие А={получить 2 попадания при пяти выстрелах} будет 10.

Применив теорему о сумме и произведении независимых событий, будем иметь:

Увеличение числа интересующих нас событий или числа испытаний приведёт к еще большему увеличению объёма вычислительных операций, поэтому возникает задача отыскания менее трудоёмких способов расчёта.

Постановка задачи:

Пусть предполагается в одинаковых условиях произвести n независимых испытаний, результатом каждого из которых может быть наступление либо события А, либо ему противоположного .

Обозначим через А₁ наступление события А при первом испытании, А₂ – при втором испытании, А_n – при последнем испытании.

В силу постоянства условий испытания:

Р(А₁) = Р(А₂) = … Р(А_n) = р

Р( ,

где:	р = Р(А)	–	вероятность наступления события А в одном испытании;
	q = )	–	вероятность наступления противоположного события в одном испытании.

Нас интересует вероятность того, что событие А при n испытаниях наступит ровно m раз, а в оставшихся n-m испытаниях – не наступит (т.е. наступит противоположное событию А событие – ).

Допустим, что интересующее нас событие А наступает подряд m раз, начиная с первого, т.е. имеет место событие – Е.

Е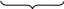 = А₁А₂ … А_m-1 А_m  (1)

m n-m

По условию повторения испытаний, события, входящие в данную комбинацию, независимы, при этом вероятности наступления событий А₁ , А₂ ,… А_m-1, А_m одинаковы и равны р: Р(А₁) = Р(А₂) =…= Р(А_m) = р, а вероятности не наступления событий так же одинаковы и равны q=1-р: .

Применяя правило умножения вероятностей для независимых событий к выражению 1 получим:

Р(Е) = Р(А₁) Р(А₂) … Р(А_m-1) Р(А_m) Р( = р^m (1-р)^{n- m} = р^mq^n-m

В силу постоянства условий испытаний мы допустили, что интересующее нас событие А наступает подряд m раз, начиная с первого. Но событие А в n испытаниях может наступить ровно m раз в различных последовательностях или комбинациях. При этом нам безразлично, в какой именно последовательности появляется событие А ровно m раз.

Число таких комбинаций равно числу сочетаний из n элементов по m.

Так как эти комбинации событий (подобные комбинации Е) несовместны и нас не интересует последовательность наступления события А в испытании ровно m раз, то обозначив интересующую нас вероятность через Р_m, получим:

Р_m = р^m (1-р)^{n - m} = =

где – число сочетаний из n элементов по m.

Данная формула носит имя формулы Бернулли.

Формула Бернулли позволяет получить ответ на вопрос: какова вероятность того, что при повторении n независимых испытаний некоторое событие А наступает ровно m раз, если в каждом из этих испытаний вероятность наступления события А постоянна и равна Р(А) = р.

Приведенная формула Бернулли имеет исключительно важное значение в теории вероятностей по той причине, что она связана с повторением испытаний в одинаковых условиях, т.е. с такими условиями, в которых как раз и проявляются законы теории вероятностей.

Заключение по лекции:

В лекции мы рассмотрели принципиальные вопросы теории вероятностей применительно к случайным величинам, ввели основной понятийный аппарат, необходимый для дальнейшего изучения дисциплины: определение случайной величины, их классификацию; понятия закона распределения и его формы для различных типов случайной величины.

В ходе подготовки к последующим лекциям и практическим занятиям вы должны самостоятельно при углубленном изучении рекомендованной литературы и решения предложенных задач дополнить свои конспекты лекций.

Кроме того, на последующих занятиях мы будем изучать теоремы и зависимости, позволяющие определить вероятность появления случайной величины требуемое число раз или на определенном интервале, например вероятность попадания в цель.