1. Формула Байеса, вероятность появления хотя бы одного события

Пусть имеется полная группа несовместных гипотез с известными вероятностями их наступления . Пусть в результате опыта наступило событие А, условные вероятности которого по каждой из гипотез известны, т.е. известны вероятности .

Требуется определить какие вероятности имеют гипотезы относительно события А, т.е. условные вероятности .

Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, делённому на полную вероятность этого события.

.

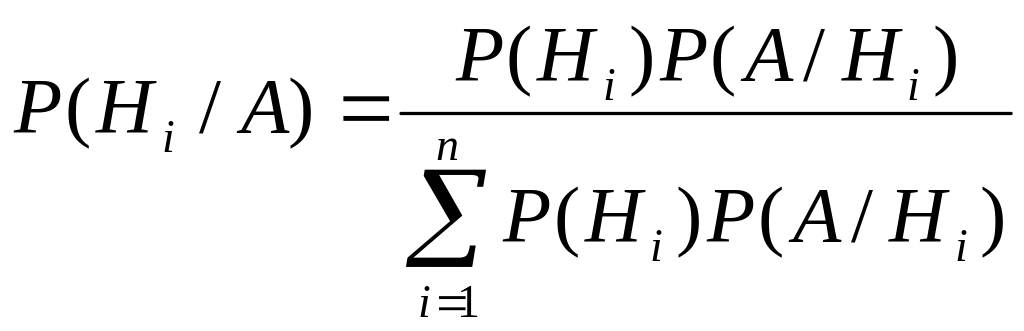Эта формула называется формулой Байеса.

Доказательство.

По Теореме умножения вероятностей получаем:

.

Тогда если .

Для нахождения вероятности P(A) используем формулу полной вероятности.

.

Если до испытания все гипотезы равновероятны с вероятностью , то формула Байеса примет вид:

.

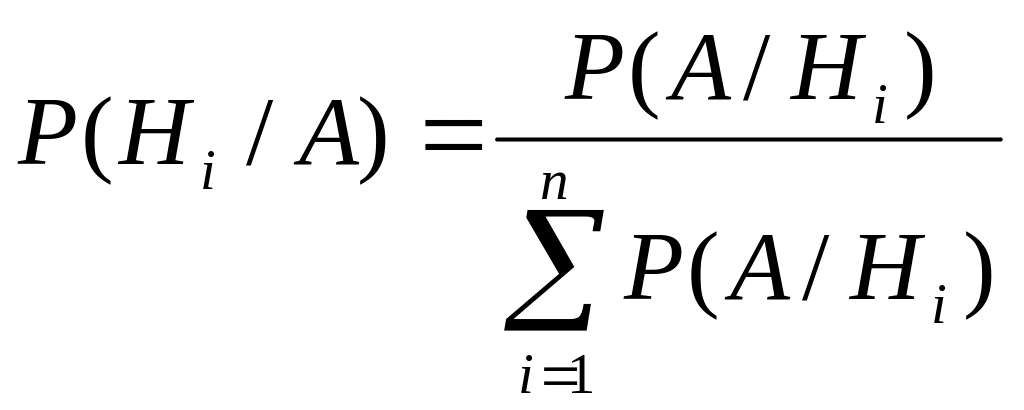Пример. Известно, что 30% приборов собирает специалист высшей квалификации, 70% приборов – специалист средней квалификации. Вероятность того, что прибор, собранный специалистом высшей квалификации, надёжен, равна 0,9. Для специалиста средней квалификации эта вероятность равна 0,8. Взятый наудачу прибор оказался надёжным. Найти вероятность того, что этот прибор собран специалистом высшей квалификации.

Решение: пусть событие – появление прибора, собранного специалистом высшей квалификации; событие – появление прибора, собранного специалистом средней квалификации. Вероятности этих событий равны соответственно ,

Пусть событие означает появление надёжного прибора. По условию примера вероятность события при условии, что появится прибор, собранный специалистом высшей квалификации, Аналогично вероятность появления надёжного прибора при условии, что появится прибор, собранный специалистом средней квалификации, Искомая вероятность появления прибора, собранного специалистом высшей квалификации, т.е. события при условии, что появилось событие определяется по формуле

Заключительная часть занятия:

• напомнить тему и учебные вопросы занятия;

• отметить степень достижения учебных целей;

• ответить на возникшие вопросы у студентов;

На занятии иметь:

Калькуляторы – на каждого

Изучить:

1. Вентцель Е.С. Теория вероятностей. Учебник. Издание восьмое, стереотипное. М.: Высшая школа, 2002 г. – 575 с., стр. 59-61.

2. Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие. Издание десятое, стереотипное. – М.: Высшая школа», 2004 г. – 480 с. стр. 55-61.

Лекция 5 Основные законы распределения дискретных случайных величин. Формула Бернулли

Учебные и воспитательные цели:

1. Ознакомить студентов с основными понятиями: случайная величина, дискретные и непрерывные случайные величины, закон распределения случайной величины.

2. Дать представление студентам о формах закона распределения случайной величины.

Вид занятия: лекция.

Продолжительность занятия: 90 минут.

Учебно-материальное обеспечение занятия:

Медиа-проектор, ноутбук, слайды Power Point (Оверхэд-проектор, слайды).