1.4. Типовой экзаменационный билет по дисциплине «Линейная алгебра»

1. Дать определение обратной матрицы. Сформулировать теорему о её единственности (2 б.).

2. Метод определителей нахождения единственного решения системы линейных уравнений (формулы Крамера) (3 б.).

3. Найти ранг матрицы при различных значениях параметра : (5 б.).

4. Исследовать и найти решение (если оно существует) системы линейных уравнений:

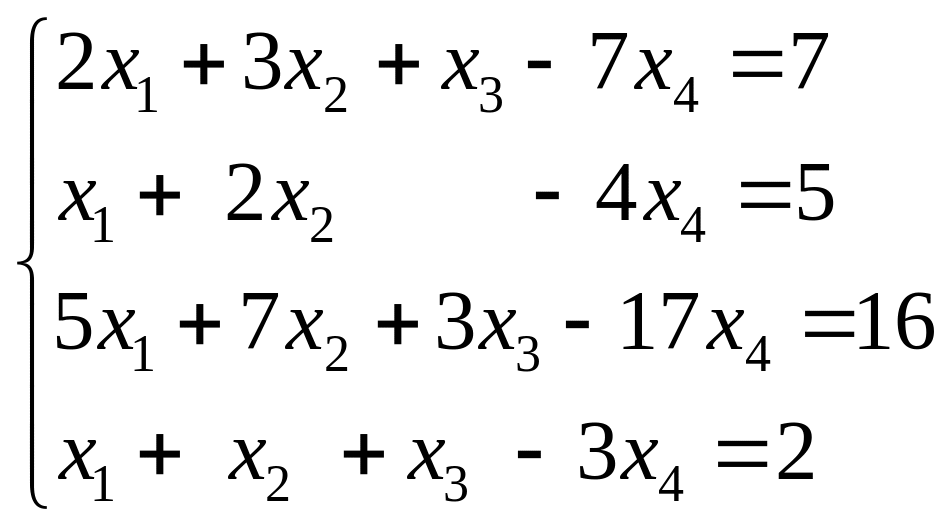(5 б.).

5. Даны две точки: А(2,3) и В(-1,0). Составить уравнение прямой, проходящей через точку В перпендикулярно отрезку АВ (5 б.).

2. Рейтинговая система контроля освоения дисциплины

Контроль освоения знаний осуществляется в соответствии с рейтинговым накопительным механизмом оценки знаний студента. Основную часть баллов студент должен заработать во время выполнения 3 рубежных аттестаций в семестре. Максимальная оценка учебной деятельности студента в течение семестра составляет 80 баллов (16 баллов – за посещение лекций; 13 баллов – за активность на практических занятиях; 12 баллов – за выполнение домашнего задания; 15 баллов – за его защиту; 24 балла – за 3 теста на интернет-тренажере). Минимальная оценка, являющаяся допуском к экзамену, составляет 50 баллов. Усвоение теоретической части дисциплины проверяется на экзамене. Максимальная рейтинговая оценка экзамена – 20 баллов. Минимальная зачетная рейтинговая оценка экзамена – 10 баллов.

Каждое посещение лекции при наличии конспекта оценивается в 1 балл. Самостоятельное решение задачи у доски на практическом занятии оценивается в 1 балл. Домашнее семестровое задание оценивается в 12 баллов, его защита – в 15 баллов (максимально возможные). Интернет-тестирование с использованием интернет-тренажеров оценивается по следующим критериям:

рейтинг теста меньше 50% – 0 баллов;

рейтинг теста 50% – min балл;

рейтинг теста 100% – max балл;

рейтинг теста от 50–100% – пересчет по формуле:

.

Максимальный и минимальный баллы конкретного теста устанавливаются преподавателем и доводятся до сведения студентов перед началом тестирования.

Таблица планирования результатов обучения по балльно-рейтинговой системе

Раздел дисциплины	Неделя проведения контроля	Оценка за модуль в баллах
		максимальная	минимальная зачетная
Модуль 1. Матрицы и СЛАУ	6	28	17
Модуль 2. Векторная алгебра и линейные пространства	11	26	17
Модуль 3. Основы аналитической геометрии	16	26	16

Шкала перевода рейтинговых оценок по всем видам занятий и самостоятельной работы в экзаменационную оценку

Баллы	Оценка	Примечания
90–100	Отлично	В разработанной системе балльной оценки всех видов работ получение отличной оценки без написания экзаменационной работы невозможно
75–89	Хорошо	Получение оценки «хорошо» без написания экзаменационной работы теоретически возможно, но для этого нужно получить максимальное количество баллов по всем текущим видам контроля
60–74	Удовлетворительно	Возможно получение этой оценки без написания экзаменационной работы, но для этого нужно получить не менее 60 баллов за текущие виды работ
Менее 60	Неудовлетворительно	С учетом того, что минимальное количество баллов за экзаменационную работу – 10, за 3 рубежные аттестации студенту в семестре необходимо набрать не менее 50 баллов, чтобы быть допущенным к экзамену