1. Оценочные средства и методики их применения
1.1. Индивидуальные домашние задания
Матрицы. Для данной матрицы A, приведенной для каждого варианта:
а) вычислить определитель матрицы A;
б) найти (если это возможно) матрицу, обратную к матрице A;
в) определить ранг матрицы A;
г) найти собственные значения матрицы A и соответствующие им собственные векторы. Записать матрицу Т, приводящую матрицу A к диагональному виду. Найти произведение матриц Т-1 A Т.
Вариант 1. 
Вариант 2. 
Вариант 3. 
Вариант 4. 
Вариант 5.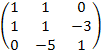 
Вариант 6. 
Вариант 7.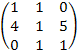 
Вариант 8.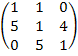 
Вариант 9.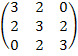 
Вариант 10. 
Вариант 11. 
Вариант 12.
Вариант 13.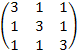 
Вариант 14. 
Вариант 15.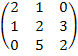 
Вариант 16.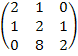 
Вариант 17. 
Вариант 18. 
Вариант 19. 
Вариант 20. 
Решить задачу «Производство – потребление».
Отрасль состоит
из двух предприятий. Известны объемы
потребления (затраты) предприятиями
выпускаемого продукта (матрица Х)
и общие объемы производства предприятий
за год, а также новый план выпуска
конечного продукта
через n
лет (конкретная величина n
не имеет значения).
1. Составить матрицу коэффициентов прямых затрат.
2. Вычислить вектор
объемов конечного продукта предприятий
при заданных объемах производства
.
3. Найти план
производства
предприятий, обеспечивающий новый план
выпуска объемов конечного продукта
через n
лет.
Указание: используйте модель Леонтьева.
Вариант 1.
Вариант 2.
Вариант 3.
Вариант 4.
Вариант 5.
Вариант 6.
Вариант 7.
Вариант 8.
Вариант 9.
Вариант 10.
Вариант 11.
Вариант 12.
Вариант 13.
Вариант 14.
Вариант 15.
Вариант 16.
Вариант 17.
Вариант 18.
Вариант 19.
Вариант 20.
Системы линейных алгебраических уравнений. Для данной системы линейных уравнений, заданной расширенной матрицей (А | b), найти общее решение и два различных базисных решения.
Вариант 1.
Вариант 2.
Вариант 3.
Вариант 4.
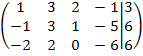
Вариант 5.
Вариант 6.
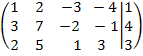
Вариант 7.
Вариант 8.
Вариант 9.
Вариант 10.
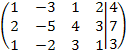
Вариант 11.
Вариант 12.
Вариант 13.
Вариант 14.
Вариант 15.
Вариант 16.
Вариант 17.
Вариант 18.
Вариант 19.
Вариант 20.
Аналитическая геометрия на плоскости.
Даны вершины треугольника АВС.
1. Найти длины сторон АВ и АС.
2. Найти точку пересечения медиан треугольника.
3. Найти угол ВАС треугольника.
4. Написать уравнения стороны АВ, высоты СD и медианы АМ треугольника.
5. Найти длину высоты СD и площадь треугольника АВС.
ВАРИАНТ № |
Координаты точек |
||
А |
B |
С |
|
1 |
9,-4 |
6,0 |
-3,5 |
2 |
-9-,4 |
-6,0 |
3,5 |
3 |
9,-4 |
12,0 |
-3,5 |
4 |
9,4 |
12,0 |
-3,-5 |
5 |
5,10 |
2,6 |
-7,1 |
6 |
-5,10 |
-2,6 |
7,1 |
7 |
5,10 |
8,6 |
-7,1 |
8 |
-5,10 |
-8,6 |
7,1 |
9 |
-6,2 |
-9,6 |
6,7 |
10 |
6,2 |
9,6 |
-6,7 |
11 |
-6,2 |
-3,6 |
6,7 |
12 |
6,2 |
3,6 |
-6,7 |
13 |
-7,-4 |
-3,-1 |
2,8 |
14 |
7,-4 |
3,-1 |
-2,8 |
15 |
-7,-4 |
-3,-7 |
2,8 |
16 |
7,-4 |
3,-7 |
-2,8 |
17 |
0,9 |
-3,5 |
9,-3 |
18 |
0,9 |
3,5 |
-9,-3 |
19 |
3,7 |
6,3 |
-6,-5 |
20 |
-3,7 |
-6,3 |
6,-5 |
Векторная алгебра и аналитическая геометрия в пространстве.
Дано: точки А, В, D, А1; числа a, b; угол φ.
1. Найти длину
вектора
,
если
– единичные векторы, угол между которыми
равен φ.
2. Найти координаты
точки М, делящей вектор
в отношении
.
3. Проверить, могут
ли векторы
и
образовывать параллелограмм, являясь
его сторонами. Найти длины этих сторон.
4. Найти углы между диагоналями параллелограмма ABCD.
5. Найти площадь параллелограмма ABCD.
6. Убедиться, что
векторы
,
и
могут
образовывать параллелепипед, являясь
его ребрами. Найти объем этого
параллелепипеда и длину его высоты.
7. Найти координаты
вектора
,
являющегося высотой параллелепипеда,
проведенной из точки А к плоскости
основания A1
B1
C1
D1;
координаты точки Н и координаты единичного
вектора, совпадающего по направлению
с вектором
.
8. Найти разложение вектора по векторам , и .
9. Найти проекцию вектора на вектор .
10. Написать уравнения плоскостей:
а) Р – проходящей через точки А, В, D;
б) Р1 – проходящей через точки А и прямую А1В1;
в) Р2 – проходящей через точки А1 параллельно плоскости Р;
г) Р3 – содержащей прямые АD и АА1;
д) Р4 – проходящей через точки А и С1 перпендикулярно плоскости Р.
11. Найти расстояние между прямыми, на которых лежат ребра АВ и СС1; написать каноническое и параметрическое уравнения общего к ним перпендикуляра.
12. Найти точку А2, симметричную точке A1 относительно плоскости основания АВСD.
ВАРИАНТ № |
А |
B |
D |
A1 |
a |
b |
φ |
1 |
1,0,0 |
1,2,0 |
0,1,0 |
0,1,2 |
5 |
-6 |
0 |
2 |
2,-1,3 |
3,-2,2 |
2,2,3 |
2,0,1 |
1 |
-1 |
π/6 |
3 |
1,0,1 |
1,2,3 |
0,1,0 |
1,0,2 |
2 |
1 |
π/2 |
4 |
1,1,1 |
0,1,0 |
0,2,1 |
2,0,3 |
3 |
2 |
2 π/3 |
5 |
0,0,-1 |
0,1,0 |
0,2,-3 |
1,0,2 |
4 |
1 |
11 π/6 |
6 |
2,0,1 |
3,-1,1 |
2,2,1 |
0,-2,3 |
5 |
-3 |
5 π/6 |
7 |
0,1,0 |
1,0,0 |
0,3,0 |
-1,2,2 |
6 |
1 |
7 π/6 |
8 |
3,-2,2 |
3,1,2 |
2,-1,3 |
3,-1,0 |
7 |
3 |
11 π/6 |
9 |
1,2,3 |
0,3,2 |
1,0,1 |
1,2,4 |
8 |
2 |
3 π/2 |
10 |
0,1,0 |
-1,2,0 |
1,1,1 |
1,0,2 |
9 |
-4 |
4 π/3 |
11 |
0,1,0 |
0,3,-2 |
0,0,-1 |
1,1,3 |
10 |
1 |
π/6 |
12 |
3,-1,1 |
3,1,1 |
2,0,1 |
1,-3,3 |
7 |
2 |
π |
13 |
0,3,0 |
0,1,0 |
1,2,0 |
-1,4,2 |
12 |
1 |
π/3 |
14 |
3,1,2 |
2,2,3 |
3,-2,2 |
3,2,0 |
13 |
-4 |
4 π/3 |
15 |
0,3,2 |
0,1,0 |
1,2,3 |
0,3,3 |
14 |
-1 |
5 π/6 |
16 |
-1,2,0 |
0,2,1 |
0,1,0 |
0,1,2 |
15 |
1 |
7 π/6 |
17 |
0,3,-2 |
0,2,-3 |
0,1,0 |
1,3,1 |
16 |
2 |
π/3 |
18 |
3,1,1 |
2,2,1 |
3,-1,1 |
1,-1,3 |
17 |
-3 |
π/4 |
19 |
1,2,0 |
0,3,0 |
1,0,0 |
0,3,2 |
18 |
2 |
π/3 |
20 |
2,2,3 |
2,-1,3 |
3,1,2 |
2,3,1 |
19 |
-2 |
5 π/3 |
Линии второго порядка.
Привести уравнение линии второго порядка к каноническому виду, определить тип этой линии и начертить ее.
Вариант 1.
x2 – 2xy + y2–10x – 6y+ +25 = 0
Вариант 2.
xy + x + y = 0
Вариант 3.
5x2 + 8xy+5y2 –18x–18y + 9 = 0
Вариант 4.
5x2 + 6xy+5y2 – 16x–16y – 16 = 0
Вариант 5.
x2 + 2xy + y2–8x + 4 = 0
Вариант 6.
5x2 + 4xy+8y2 – 32x–56y + 80 = 0
Вариант 7.
5x2 + 12xy–22x – 12y–19 = 0
Вариант 8.
4x2 – 12xy+9y2 – 2x+3y – 2 = 0
Вариант 9.
4xy + 3y2+16x + 12y–36 = 0
Вариант 10.
2x2 + 4xy+5y2 – 6x–8y – 1 = 0
Вариант 11.
x2 – 2xy + y2–10x – 6y+ +25 = 0
Вариант 12.
xy + x + y = 0
Вариант 13.
5x2 + 8xy+5y2 –18x–18y + 9 = 0
Вариант 14.
5x2 + 6xy+5y2 – 16x–16y – 16 = 0
Вариант 15.
x2 + 2xy + y2–8x + 4 = 0
Вариант 16.
5x2 + 4xy+8y2 – 32x–56y + 80 = 0
Вариант 17.
5x2 + 12xy–22x – 12y–19 = 0
Вариант 18.
4x2 – 12xy+9y2 – 2x+3y – 2 = 0
Вариант 19.
4xy + 3y2+16x + 12y–36 = 0
Вариант 20.
2x2 + 4xy+5y2 – 6x–8y – 1 = 0
Квадратичные формы.
1. Привести квадратичную форму F(x,y,z) к каноническому виду.
2. Определить знакоопределенность квадратичной формы.
Вариант 1.
F(x, y, z) = 4x2 + 6y2+4z2 + 4xz – 8y–4z + 3
Вариант 2.
F(x, y, z) = x2 + 5y2+z2 + 2xy + 6xz +2yz–2x + 6y–10z
Вариант 3.
F(x, y, z) = x2 + y2–3z2 – 2xy – 6xz–6yz + 2x + 2y + 4z
Вариант 4.
F(x, y, z) = x2 – 2y2+z2 + 4xy – 8xz – 4yz–14x – 4y + 14z + 16
Вариант 5.
F(x, y, z) = 2x2 + y2+2z2 – 2xy – 2xz + x–4y – 3z + 2
Вариант 6.
F(x, y, z) = x2 – 2y2+z2 + 4xy – 10xz+4yz + x + y – z
Вариант 7.
F(x, y, z) = 2x2 + y2+2z2 – 2xy – 2xz+4x – 2y
Вариант 8.
F(x, y, z) = x2 + y2–4z2 + 2xy + 4xz+4yz – 6z + 1
Вариант 9.
F(x, y, z) = 4xy+2x + 4y – 6z – 3
Вариант 10.
F(x, y, z) = xy + xz+ yz+ 2x + 2y – 2z
Вариант 11.
F(x, y, z) = 4x2 + 6y2+4z2 + 4xz – 8y–4z + 3
Вариант 12.
F(x, y, z) = x2 + 5y2+z2 + 2xy + 6xz +2yz–2x + 6y–10z
Вариант 13.
F(x, y, z) = x2 + y2–3z2 – 2xy – 6xz–6yz + 2x + 2y + 4z
Вариант 14.
F(x, y, z) = x2 – 2y2+z2 + 4xy – 8xz – 4yz–14x – 4y + 14z + 16
Вариант 15.
F(x, y, z) = 2x2 + y2+2z2 – 2xy – 2xz + x–4y – 3z + 2
Вариант 16.
F(x, y, z) = x2 – 2y2+z2 + 4xy – 10xz+4yz + x + y – z
Вариант 17.
F(x, y, z) = 2x2 + y2+2z2 – 2xy – 2xz+4x – 2y
Вариант 18.
F(x, y, z) = x2 + y2–4z2 + 2xy + 4xz+4yz – 6z + 1
Вариант 19.
F(x, y, z) = 4xy+2x + 4y – 6z – 3
Вариант 20.
F(x, y, z) = xy + xz+ yz+ 2x + 2y – 2z