ПРИЛОЖЕНИЕ 1
Индивидуальные домашние задания содержат 10 тем для 10 вариантов.
Пределы. Требуется вычислить пределы функций.
Вариант 1.
Вариант 2.
Вариант 3.
Вариант 4.
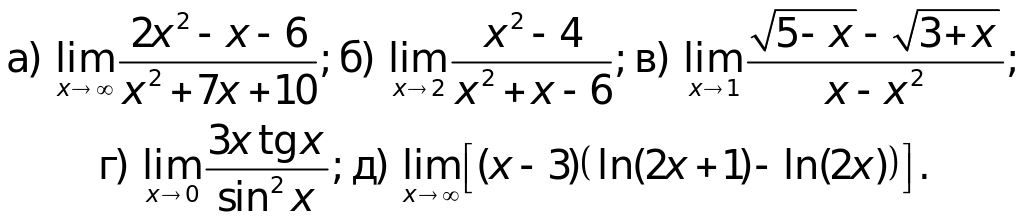
Вариант 5.
Вариант 6.
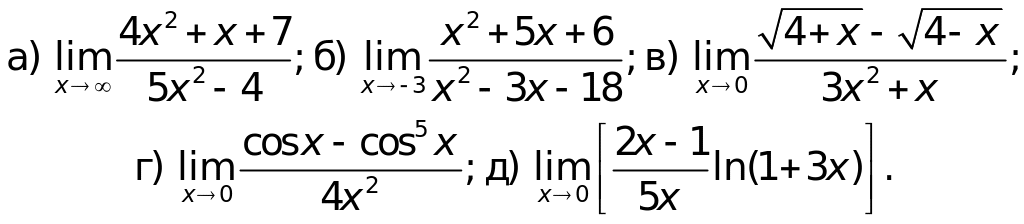
Вариант 7.
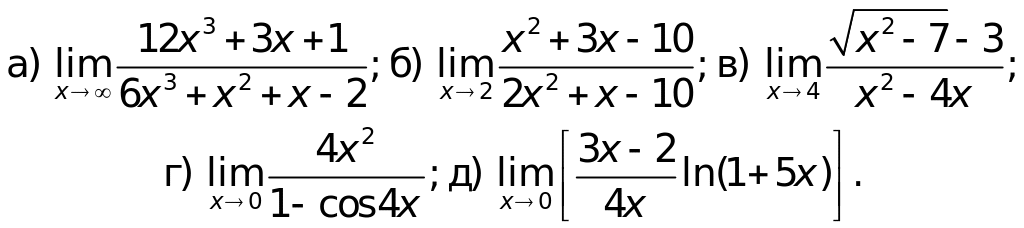
Вариант 8.
Вариант 9.
Вариант 10.
Производные. Требуется вычислить производные функций.
Вариант 1.
Вариант 2.
Вариант 3.
Вариант 4.
Вариант 5.
Вариант 6.
Вариант 7.
Вариант 8.
Вариант 9.
Вариант 10.
Применение производной к исследованию функций. Требуется исследовать функцию и построить ее график.
Вариант 1.
Вариант 2.
Вариант 3.
Вариант 4.
Вариант 5.
Вариант 6.
Вариант 7.
Вариант 8.
Вариант 9.
Вариант 10.
Производная по направлению и градиент. Требуется найти в точке A производную функции f(x, y) по направлению a.
Вариант 1.
Вариант 2.
Вариант 3.
Вариант 4.
Вариант 5.
Вариант 6.
Вариант 7.
Вариант 8.
Вариант 9.
Вариант 10.
Экстремумы функций нескольких переменных. Требуется найти наибольшее и наименьшее значения функции f(x, y) в области, ограниченной заданными линиями.
Вариант 1.
Вариант 2.
Вариант 3.
Вариант 4.
Вариант 5.
Вариант 6.
Вариант 7.
Вариант 8.
Вариант 9.
Вариант 10.
Неопределенный интеграл. Требуется вычислить неопределенный интеграл.
Вариант 1.
Вариант 2.
Вариант 3.
Вариант 4.
Вариант 5.
Вариант 6.
Вариант 7.
Вариант 8.
Вариант 9.
Вариант 10.
Определенный интеграл. Требуется вычислить определенный интеграл.
Вариант 1.
Вариант 2.
Вариант 3.
Вариант 4.
Вариант 5.
Вариант 6.
Вариант 7.
Вариант 8.
Вариант 9.
Вариант 10.
Применение определенного интеграла к вычислению площадей. Требуется вычислить площадь фигуры, ограниченной двумя линиями.
Вариант 1.
Вариант 2.
Вариант 3.
Вариант 4.
Вариант 5.
Вариант 6.
Вариант 7.
Вариант 8.
Вариант 9.
Вариант 10.
Дифференциальные уравнения. Требуется найти общее решение или общий интеграл дифференциального уравнения.
Вариант 1.
Вариант 2.
Вариант 3.
Вариант 4.
Вариант 5.
Вариант 6.
Вариант 7.
Вариант 8.
Вариант 9.
Вариант 10.
Ряды. Требуется исследовать сходимость ряда.
Вариант 2.
Вариант 3.
Вариант 4.
Вариант 5.
Вариант 6.
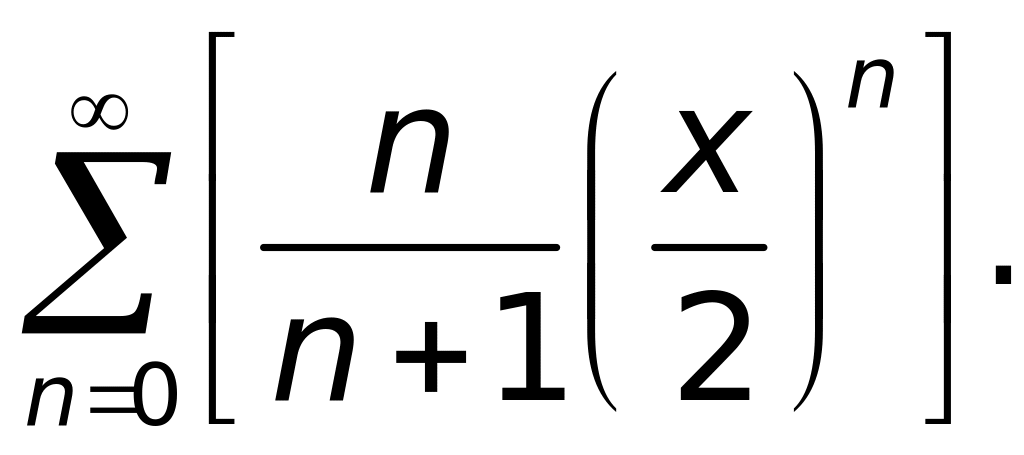
Вариант 7.
Вариант 8.
Вариант 9.
Вариант 10.
Типовая аттестационная работа № 1
Найти предел последовательности
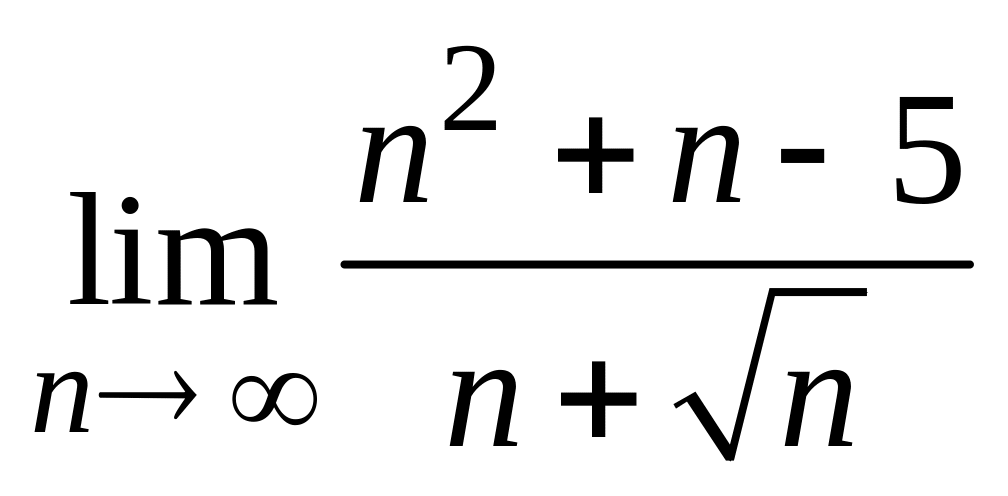.Для данных комплексных чисел z1 = 7 + i, z2 = –5 + 2i вычислить z1 + z2, z1 – 2z2,
,
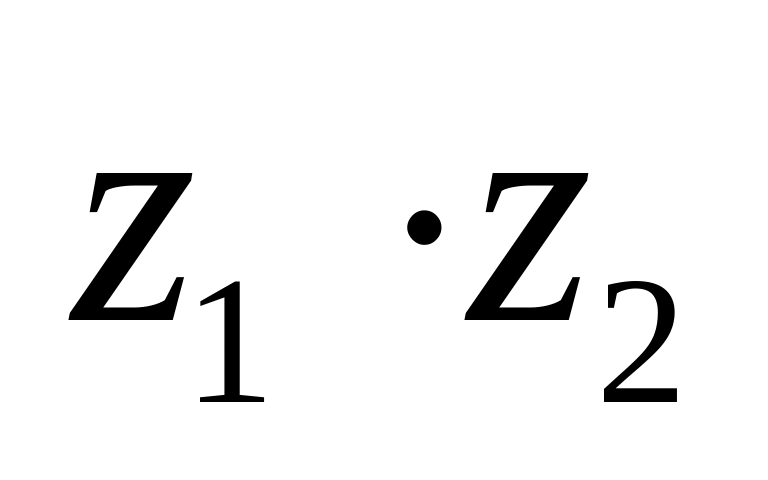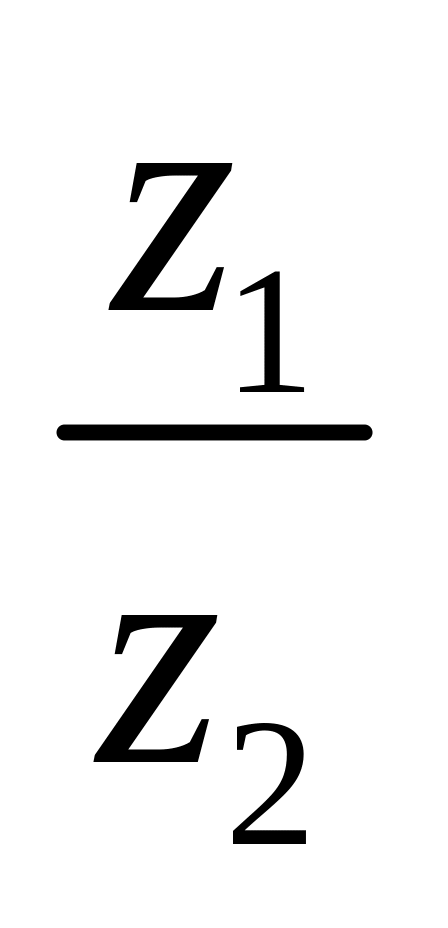.Найти левый и правый пределы функции
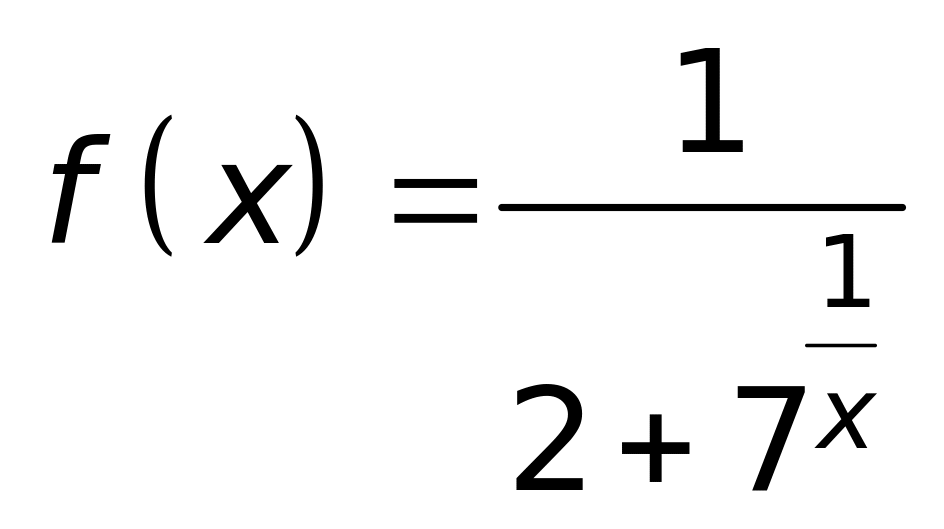в точке
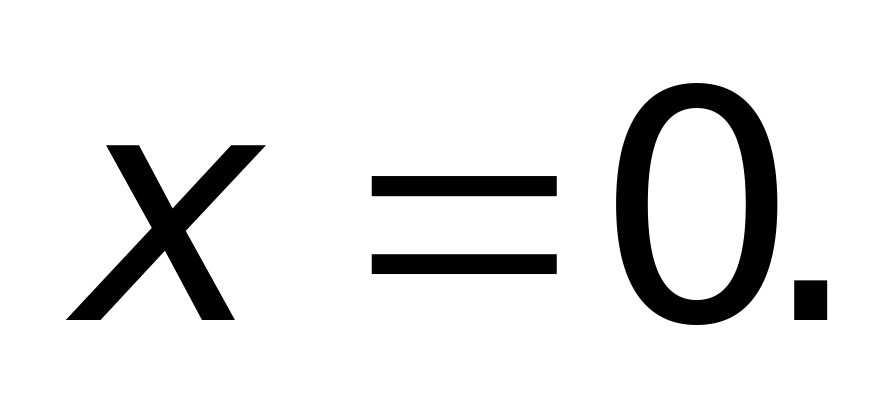
Найти точки разрыва функции
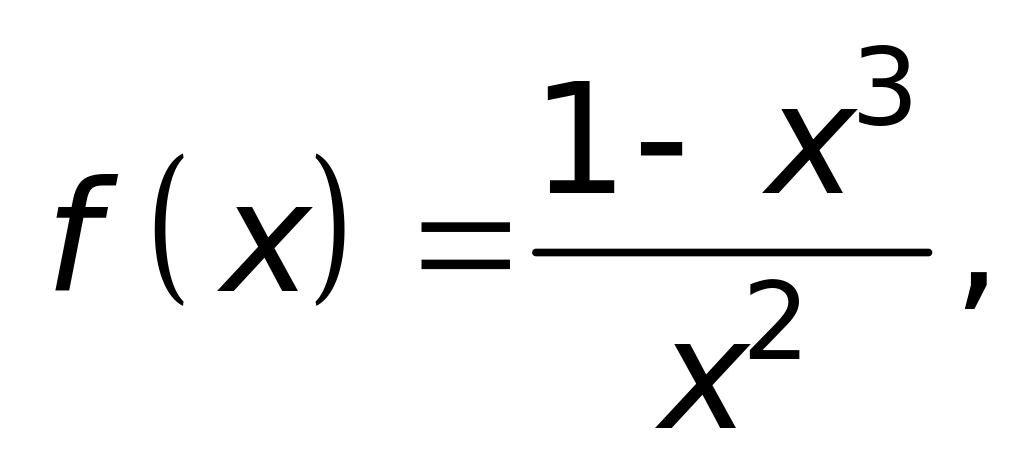определить их тип и построить схематический
график.
Типовая аттестационная работа № 2
1.
Вычислить
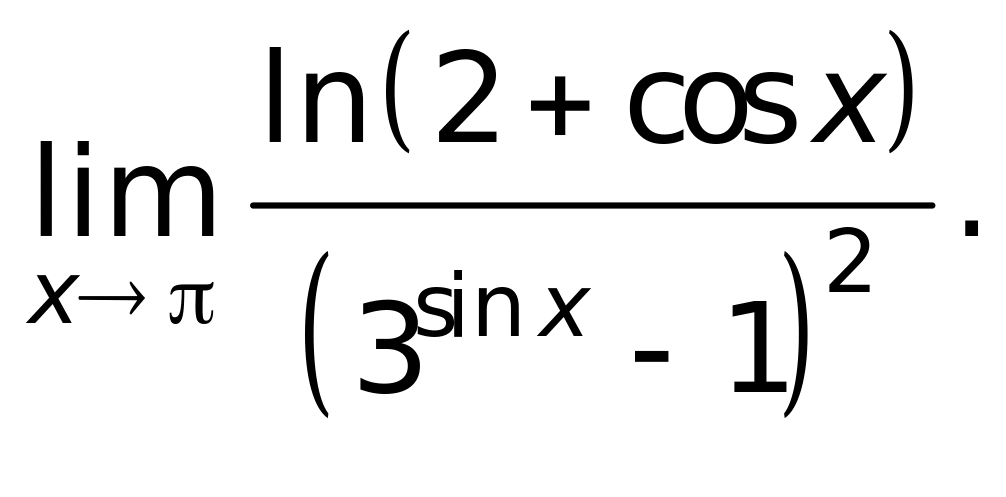
2. Вычислить
дифференциал функции
в точке x0 = 1.
3. С помощью
дифференциала первого порядка вычислить
приближенно
.
4. Найти все частные
производные второго порядка для функции
в точке (1, 2).
Типовая аттестационная работа № 3
1.
Вычислить интеграл на некотором
промежутке X
из области определения подынтегральной
функции:
.
2. Вычислить
определенный интеграл
.
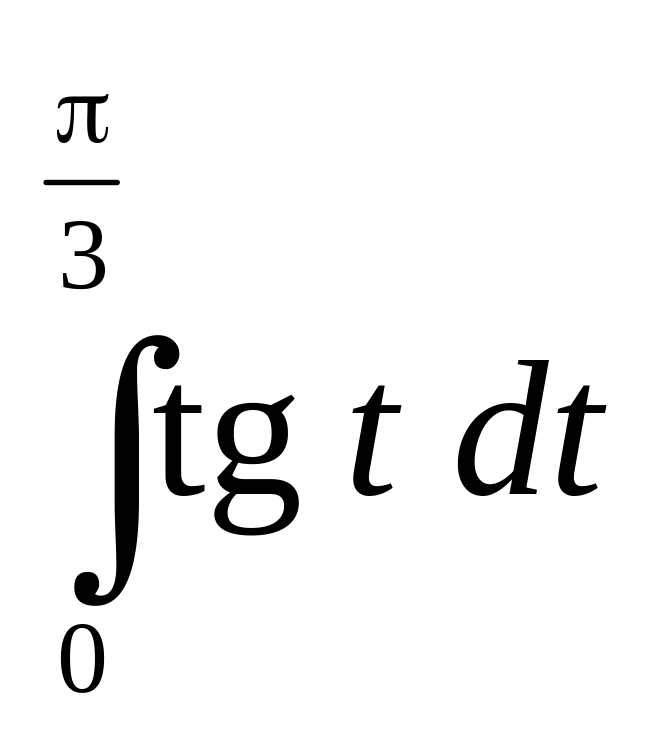3.
Вычислить площадь криволинейной
трапеции, ограниченной кривыми v(x) = 0,
и прямыми x = 0,
x = 1.
Вопросы к экзамену
Общее понятие функции. Функция одной переменной.
Способы задания функций: аналитический, графический, табличный.
График функции. Свойства функций одной переменной: четность, монотонность, выпуклость, периодичность.
Элементарные функции: линейная функция, парабола, гипербола, многочлены.
Элементарные функции: степенная, показательная, логарифмическая.
Последовательности и ряды чисел, предел последовательности и сумма ряда, монотонные, ограниченные последовательности. Геометрическая и арифметическая прогрессии.
Предел функции. Основные свойства пределов.
Бесконечно малые и бесконечно большие функции. Сравнение бесконечно малых.
Первый и второй замечательные пределы.
Непрерывность функции в точке и на множестве. Классификация точек разрыва.
Асимптоты графика функции.
Производная функции и ее геометрический смысл. Свойства производной.
Дифференцируемость функции, первый дифференциал.
Производные основных элементарных функций.
Производная сложной функции и неявно заданных функций.
Инвариантность первого дифференциала.
Производные и дифференциалы высших порядков.
Свойства дифференцируемых функций.
Лемма Ферма.
Теоремы Ролля и Лагранжа.
Правило Лопиталя раскрытия неопределенностей.
Формула Тейлора.
Монотонность функции. Условия монотонности.
Экстремум функции. Необходимые и достаточные условия экстремума.
Выпуклость графика функции. Точки перегиба.
Общая схема исследования функции и построение графика с помощью дифференциального исчисления.
Функция нескольких переменных как функция от точки в линейном пространстве.
Графическое и аналитическое описание функции нескольких переменных.
Пространственный график функции двух переменных. Линии и поверхности уровня.
Полное и частные приращения функции. Частные производные.
Дифференцируемость функции нескольких переменных, первый дифференциал, его геометрический смысл.
Производная по направлению.
Градиент и его геометрический смысл.
Производные и дифференциалы высших порядков.
Формула Тейлора для функции нескольких переменных.
Необходимые условия экстремума. Достаточное условие для случая двух независимых переменных.
Условный экстремум. Метод множителей Лагранжа.
Неопределенный интеграл и его свойства.
Основные приемы интегрирования: замена переменной, интегрирование по частям.
Табличное интегрирование. Интегрирование простейших рациональных функций. Рационализация интегрируемой функции.
Интегралы, не выражающиеся в элементарных функциях (интеграл вероятности и др.).
Определенный интеграл как предел интегральных сумм.
Свойства определенного интеграла: линейность, аддитивность, теорема о среднем.
Среднее значение функции.
Интеграл с переменным верхним приделом. Формула Ньютона–Лейбница. Замена переменной и интегрирование по частям в определенном интеграле.
Определение несобственных интегралов.
Дифференциальные уравнения. Общее решение дифференциального уравнения. Частные решения дифференциального уравнения. Задача с начальными условиями (задача Коши).
Приближенное решение задачи Коши (метод ломаных Эйлера).
Дифференциальные уравнения с разделяющимися переменными.
Однородные уравнения первого порядка.
Линейное дифференциальное уравнение первого порядка.
Уравнение Бернулли.
Числовые ряды. Сходимость числового ряда. Необходимое условие сходимости.
Гармонический ряд и ряд геометрической прогрессии.
Признаки сходимости знакопостоянных рядов.
Знакочередующиеся ряды.
Абсолютная и условная сходимость. Признак Лейбница.
Степенные ряды. Область сходимости.