Vshir ( [ [ V | Way ] | _ ], [ V | Way ] ) :- % Голова списка – полученное решение

my_goal ( V ). % Цель достигнута

vshir ( [ [ V | Way ] | Ways ], Resh ) :-

% New_ways - все продолжения пути на один шаг

findall ( X, kandidat ( [ V | Way ], X ), New_ways ),

conc ( Ways, New_ways, Ways1 ), !, % Добавление в конец множества кандидатов

vshir ( Ways1, Resh );

Vshir ( Ways, Resh ). % Продолжение поиска в случае тупикового пути

kandidat ( [ B | Way ], [ B1, B | Way ] ) :-

posle ( B, B1 ),

not ( member ( B1, [ B | Way ] ) ). % Обнаружение зацикливания

member ( X, [ X | _ ] ).

member ( X, [ _ | T ] ) :- member ( X, T ).

conc ( [ ], L, L ).

conc ( [ X | L1 ], L2, [ X | L3 ] ) :-

conc ( L1, L2, L3 ).

goal user_interface ( a, Resh ), write ( Resh ).

Обе эти стратегии (поиск в глубину и поиск в ширину) обносятся к так называемым алгоритмам полного перебора пространства состояний. Они способны получить оптимальное решение, но время получения решения может оказаться неприемлемым. Более изощренные процедуры поиска используют какую-либо дополнительную информацию, отражающую специфику задачи, с тем, чтобы на каждой стадии поиска принимать решение о наиболее перспективных путях поиска. Дополнительная информация, относящаяся к конкретной решаемой задаче, используемая для управления поиском, называется эвристикой, а алгоритмы, использующие эвристику – эвристическими. Эвристические алгоритмы могут быть реализованы как на базе поиска в глубину, так и в ширину.

Рассмотрим детальную реализацию поиска пути на графе на базе алгоритма поиска в глубину. После несложного расширения эта программа сможет отвечать на следующие вопросы:

- как добраться из одной вершины в другую, не посещая дважды одной и той же вершины;

- как пройти по маршруту, посетив заданную вершину;

- как добраться до нужной вершины, избежав некоторых вершин.

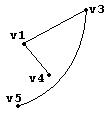
Рис. Граф, представляющий фрагмент пространства состояний

Пусть имеется следующий граф, представляющий фрагмент пространства состояний.

Центральной частью программы будет база данных (факты), содержащая данные о сети дуг между вершинами. Эта информация представлена в виде двухаргументного отношения road, например:

road( v1, v3 ).

road( v4, v1 ).

road( v3, v5 ).

Необходимо иметь информацию об обратных направлениях. Вместо того, чтобы переписывать факты, воспользуемся правилом road1:

road1( T1, T2 ) :– road( T1, T2 );

road( T2, T1 ).

Для решения этой задачи удобнее всего собирать в список все пройденные вершины. Будем исходить из следующих соображений: если существует дуга из вершины X в вершину Y, то путь найден (базовое правило), иначе чтобы найти путь из X в Y, надо найти дугу из X в Z и затем путь из Z в Y (рекурсивное правило):

way(X,Y,[ ]):–road1(X,Y).

way(X,Y,[Z|W]):–road1(X,Z), way(Z,Y,W).

Очевиден недостаток такой записи: система, не смущаясь, будет находить маршруты, многократно проходящие через одну и ту же вершину. Чтобы избежать этого зацикливания, следует добавить проверку непринадлежности очередной вершины найденному списку вершин:

way(X,Y,[Z|W]]):- road1(X,Z), way(Z,Y,W), not(member(Z,W)).

Здесь member – знакомый предикат проверки принадлежности элемента списку.

Рекурсия неизбежно становится нехвостовой, поскольку для предиката member необходимо иметь конкретизированную величину списка W (а список этот конкретизируется только при обратном прохождении рекурсии). Но в такой рекурсии опасность зацикливания не устранена: можно без конца совершать переходы из одной вершины в другую и обратно, т.к. до проверки не принадлежности вершины маршруту вычисления просто не доходят. Очевидна необходимость хвостовой рекурсии. Можно перейти к такой рекурсии, если начать вычисления от конкретизированного списка (например, пустого) и иметь уже тем больший список, чем больше вложенность рекурсии, т.е. накапливать список в правой части правила. Но в таком случае накопленный список надо зафиксировать в базовом правиле введением дополнительного аргумента:

way(X,Y,W,W):–road1(X,Y).

way(X,Y,W,L):– road1(X,Z), not(member(Z,W)),

way(Z,Y,[Z|W],L).

Для запуска этой программы можно воспользоваться интерфейсным предикатом go, аргументы которого содержат начальный и конечный пункты:

go(Here,There):– way(Here,There,[Here],W),

add(There,W,W1), reverse(W1,W2), write(W2).

Здесь исходный список маршрута конкретизируется начальной вершиной. К списку найденного маршрута добавляется конечный пункт (предикат add). Предикат reverse выполняет инверсию этого списка. Клозы этих последних предикатов было записано ранее.

Для нахождения пути из одного заданного города в другой следует при запуске цели конкретизировать переменные Here и There. Если требуется найти путь для двух конкретных городов, проще всего ввести значения переменных стандартным предикатом Readln. В некоторых задачах необходимо организовать перебор в пространстве вершин. Наиболее корректное решение в этом случае – получить список всех вершин, а затем последовательно конкретизировать переменные вершинами из этого списка, например, с помощью предиката member или away. Вершины можно собрать в список с помощью стандартного предиката findall, использовав базу данных (фактов) задачи (см. раздел «Стандартные предикаты»).