3.4.8. Обращение списка

Определим предикат

reverse( L1, L2 ).

Аргументы L1 и L2 – два списка, из которых список L2 содержит элементы списка L1, записанные в обратном порядке.

reverse( L1, L2 ):– reverse1( L1, [ ], L2 ).

reverse1( [ ], L, L ).

reverse1( [ H | T ], L1, L2 ):– reverse1( T, [ H | L1 ], L2 ).

Предикат reverse в данном случае является интерфейсным, он запускает в работу основной рабочий предикат reverse1, имеющий дополнительный второй аргумент – список, который вначале пуст, и используется собственно для обращения списка. На каждом шаге рекурсии один элемент исходного списка становится головой промежуточного списка. Третий аргумент передается от шага к шагу и конкретизируется в момент достижения базового состояния предиката reverse1. Когда первый список исчерпан, второй уже содержит элементы, записанные в обратном порядке. Отметим, что наличие третьего аргумента, фиксирующего результат, обязательно, т.к. после обратного прохождения рекурсии все конкретизированные переменные принимают свои первоначальные значения. Проследить работу этого предиката можно, если его расписать, как в предыдущем примере.

3.4.9. Нахождение максимального элемента списка

Здесь нам понадобится вспомогательный предикат max, выбирающий максимальное значение из двух элементов:

max( X, Y, X ):– X >= Y.

max( X, Y, Y ):– X < Y.

Результативный предикат maxlist(LIST, MAX), где MAX – наибольший элемент списка LIST, выглядит следующим образом:

maxlist( [ X ], X ).

maxlist( [ X, Y | TAIL ], MAX ) :–

maxlist( [ Y | TAIL ], MAXTAIL ),

max( X, MAXTAIL, MAX ).

Смысл базового правила: максимальный элемент одноэлементного списка равен самому этому элементу. Иначе, если в списке есть хотя бы два элемента X и Y, выбирается максимальный элемент хвоста MAXTAIL и при этом MAX равен наибольшему из X и MAXTAIL. Рекурсия здесь нехвостовая, чтобы обеспечить конкретизацию переменных X и MAXTAIL.

3.4.10. Перестановки

В различных логических задачах часто требуется строить перестановки элементов некоторого заданного списка. Для этого определим отношение permutation двумя аргументами. Аргументы – это два списка, один из которых является перестановкой другого.

Программирование отношения permutation основывается на рассмотрении двух случаев:

(1) Если первый список пуст, то и второй список должен быть пустым.

(2) Если первый список не пуст, тогда он имеет вид [ X | L ], и перестановку такого списка можно построить так: вначале получить перестановку списка L1, а затем внести X в произвольную позицию L1.

Два прологовских предложения, соответствующие этим случаям, таковы:

permutation ( [ ], [ ] ).

permutation ( [ X | L ], P ) :-

permutation ( L, L1 ),

add2( X, L1, P ).

Программирование отношения permutation можно реализовать и другим способом, если вспомнить, что отношение «внести» программируется через «удалить».

3.4.11. Примеры использования списков

Программирование рекурсивных предикатов работы со списками как основными структурами данных представляет собой увлекательное занятие.

Пролог идеально подходит для решения различного рода математических ребусов и головоломок, требующих перебора. При этом пространство состояний удобно представлять в виде списков, из которого можно «черпать» элементы. Рассмотрим одну такую головоломку.

Т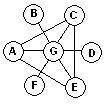 ребуется расставить в кружочках числа от 1 до 25 таким образом, чтобы каждая сумма по каждой диагонали была равна 25 и сумма вершин треугольника тоже бы равнялась 25. Разным буквам должны соответствовать разные числа, иначе возможно тривиальное решение.

Список чисел, из которого будут конкретизироваться переменные, определим как факт cifr. Введем отношение summa, аргументами которого будут семь переменных, которые предстоит конкретизировать с выполнением заданных условий. В программе действия по конкретизации переменных выполняет предикат удаления элемента из списка away. Это трехаргументное отношение, в котором в нашем примере конкретизирован второй аргумент – список доступных чисел. Предикат конкретизирует число из этого списка и возвращает третий аргумент – список без удаленного числа. Путем последовательных удалений будут конкретизированы все числа.

Полная программа для решения головоломки приводится ниже.

Domains

i = integer

ILIST= i *

predicates

summa( i, i, i, i, i, i, i, ILST )

away( i, ILIST, ILIST )

cifr( ILIST )

clauses

cifr([1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]). % Столько чисел хватит

summa( A, B, C, D, E, F, G, CIF ) :-

away( A, CIF, CIF1 ),

away( B, CIF1, CIF2 ),

away( C, CIF2, CIF3 ),

away( D, CIF3, CIF4 ),

away( E, CIF4, CIF5 ),

away( F, CIF5, CIF6 ),

away( G, CIF6, _ ),

A + G + D = 25,

B + G + E = 25,

C + G + F = 25,

A + C + E = 25.

away( A, [ A | L ], L ).

away( A, [ B | L ], [ B | L1 ] ):-

away( A, L, L1 ).

goal cifr( CIF ), % Переменная CIF конкретизируется списком чисел

summa( A, B, C, D, E, F, G, CIF ), write( A, B, C, D, E, F, G ).

В данном случае у нас найдено только одно решение. Для получения всех решений следует включить бэктрекинг (см. «Организация циклов»).