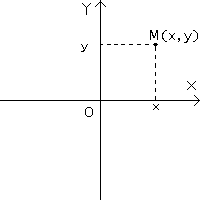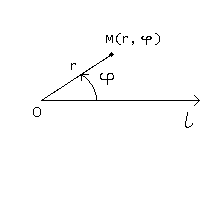2.2 Алгебраическая и тригонометрическая форма записи комплексных чисел. Показательная форма записи комплексных чисел (формула Эйлера).

Подставим в выражения (8), тогда получаем . (9)

— называется тригонометрической формой комплексного числа z.

По формуле Эйлера подставляя в (9) получим формулу

(10)

которая называется показательной формой комплексного числа.

 Запишем число в тригонометрической форме. Для этого надо найти модуль и аргумент этого числа.

Комплексная точка лежит в первой четверти и .

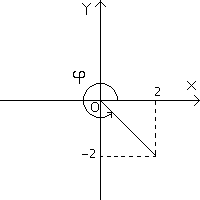
Таким образом, в тригонометрической форме .

Рассмотрим . Для него ,

Главное значение аргумента равно 270^+45^=315^.

.

Самостоятельно найдите тригонометрическую форму чисел и .

2.3 Алгебраические действия с комплексными числами.

Пусть даны два комплексных числа и .

 Суммой (разностью) двух комплексных чисел называют комплексное число

Например, .

 Произведением двух комплексных чисел и называется комплексное число

 Найдите произведение комплексно сопряженных чисел ,

 Отношением двух комплексных чисел называется комплексное число

 Найдите отношение на

 Произведение и отношение комплексных чисел удобно находить в тригонометрической форме. Пусть , а .Тогда

,

.

 Выполнить действие над комплексными числами , , в алгебраической и тригонометрических формах.

, , .

• Для извлечения корня n-ой степени из комплексного числа в тригонометрической форме используется формула, дающая n значений этого корня:

(11)

где — арифметический корень из модуля z, а n=0, 1, 2, …, (n-1).

 Вычислить .

Решение. Найдем модуль и аргумент данного числа.

, ;

поскольку x<0, y>0, то число находится во второй четверти комплексной плоскости.

, ,

По формуле (11)

, k=0, 1, 2.

Отсюда

2.4 Полярная система координат. Ее связь с декартовой системой координат.

Если на плоскости задана прямоугольная система координат, то любую точку этой плоскости обозначают , где x,y — координаты этой точки.

Зададим другую систему координат: точку О — называемую полюсом и положительное направление оси (называемой полярной осью) ol.

Тогда положение любой точки плоскости можно характеризовать следующими двумя координатами: ее расстоянием до точки O и углом наклона отрезка OM к полярной оси. То есть точка M имеет две координаты: расстояние до полюса — r и угол наклона отрезка OM к полярной оси — .

Если совместить начало координат декартовой системы координат с полюсом, то

(12)

(12) — формулы перехода от декартовых координат к полярным.

Задачи для самостоятельного решения.

1. Даны матрицы:

1. Вычислить: |A|, |B|, |C|, |G|, |F|

2. Найти сумму: A+B, A+C, A+B+C

3. Найти: , ,

4. Найти произведение: , ,

5. Найти обратные матрицы , ,

2. Решить системы уравнений по формулам Крамера, методом Гауcса и матричным методом:

   1. 

2. 

3. Даны комплексные числа , .

   1. Вычислить: z ₁+z₂, z₁+z₂, z₁z₂,

2. Преобразовать к тригонометрической форме и вычислить: , , ,

22