1.1.6. Алгебра матриц: сложение, умножение на число, произведение матриц.
Пусть даны две матрицы A и B.
Суммой
(разностью)
матриц A
и B
называется матрица C,
элементы которой
,
где
ij,
bij
элементы матриц A
и B
соответственно.
Сумма (разность) определяется только для матриц одинаковой размерности.
Сложите:
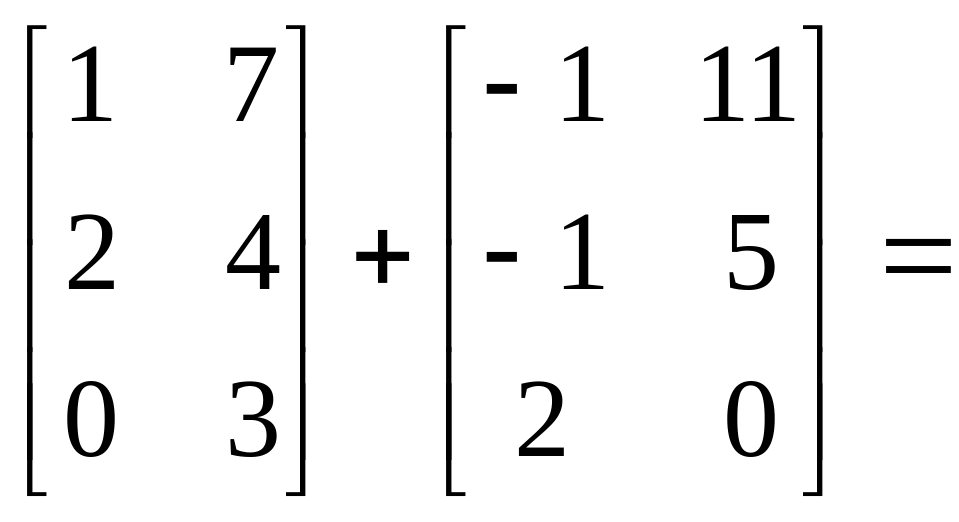
При умножении
матрицы A
на число
нужно все элементы матрицы A
умножить на это число.
Пусть =-2,
.
A=
Произведением
матриц Amxn
и Bnxp
называется матрица Cmxp,
элементы которой вычисляются по формуле
,
для
i=1,2,
…, m;
j=1,2,
…, p.
В общем случае
,
а иногда и вовсе не определено.
Пусть
,
.
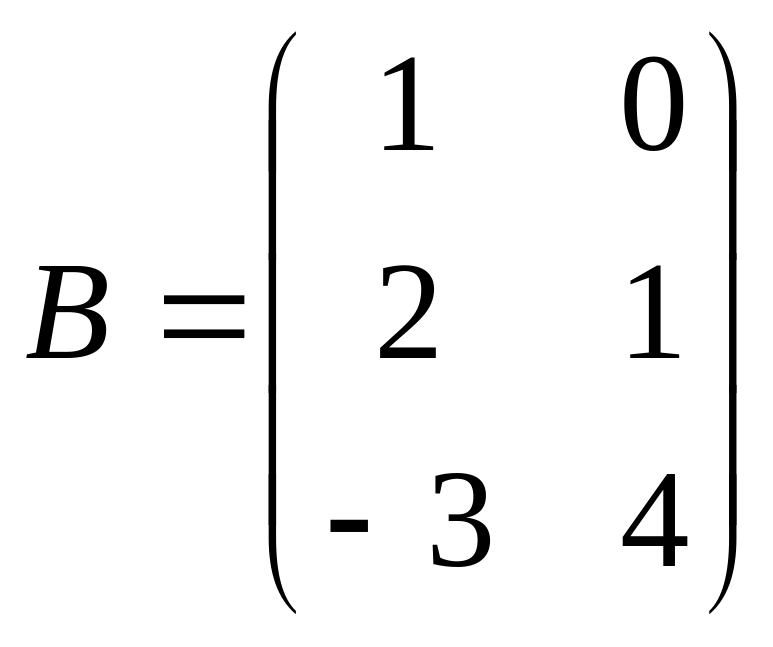Найти
.
,
где
Самостоятельно
найдите
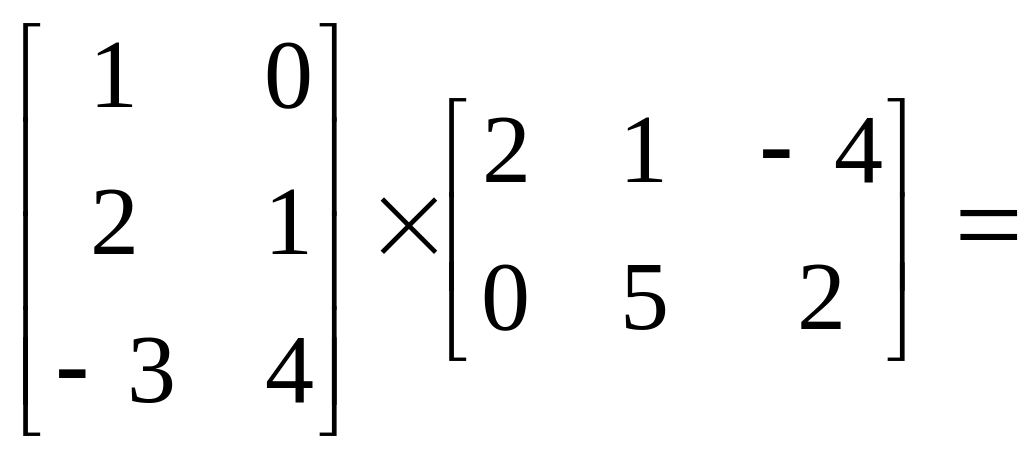
1.1.7. Обратная матрица.
Матрица А-1
называется обратной для невырожденной
матрицы A,
если:
,
где E
— единичная матрица. Для квадратной
невырожденной матрицы третьего порядка
обратная матрица находится по формуле:
,
где A11,
A12,
…, A33
— алгебраические дополнения элементов
матицы A.
Найти обратную
для матрицы
,
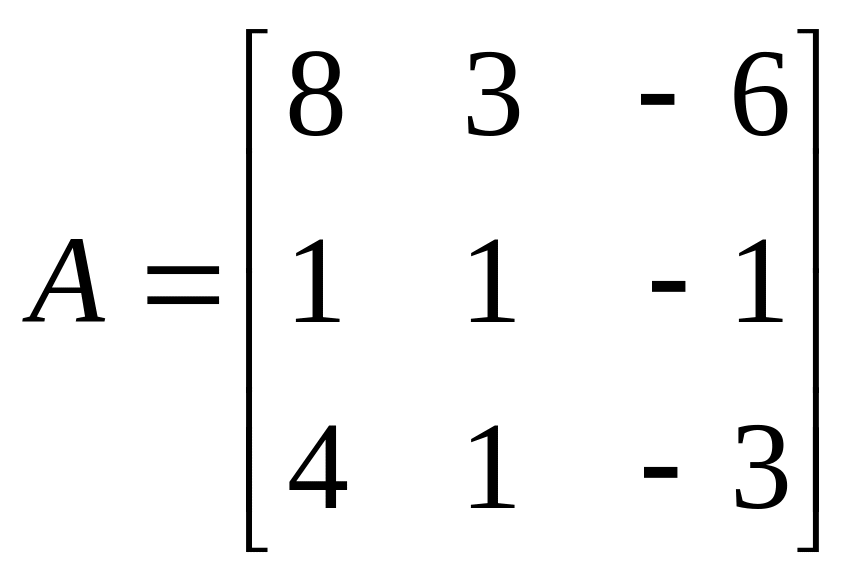
поэтому для A
существует обратная матрица A-1,
для ее нахождения вычислим все
алгебраические дополнения элементов
матрицы
A11= |
|
A21= |
|
A31= |
|
A12= |
|
A22= |
|
A32= |
|
A13= |
|
A23= |
|
A33= |
|
Таким образом, обратная к матрице A матрица:
Ранг матрицы
Рангом матрицы называется наибольший порядок отличного от нуля определителя, порожденного данной матрицей.
При вычислении ранга матрицы производят те же преобразования, что и при вычислении определителя
Найти ранг матрицы.
,
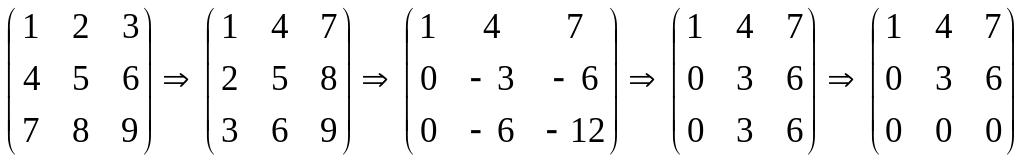r
(ранг) =2
- ранг матрицы фактически равен числу отличных от нуля элементов, примыкающих к гипотенузе нулевого треугольника.
1.2. Системы линейных уравнений.
Система трех линейных уравнений с тремя неизвестными x1 , x2, x3 имеет вид:
|
(5) |
Где ij — коэффициенты системы; bi — свободные члены.
Определитель третьего порядка , составленный из коэффициентов при неизвестных, называется определителем системы.
Обозначим его , а 1, 2, 3 – определители, полученные из соответственно вычеркиванием первого, второго и третьего столбцов и заменой их столбцом свободных членов.
|
(6) |
,
,
,
1.2.1. Решение систем линейных алгебраических уравнений по формулам Крамера.
Если для системы
уравнений (5)
,
то система имеет единственное решение,
которое находится по следующим формулам,
называемым формулами (или правилом)
Крамера:
,
,
,
где все определители вычисляются по
формулам (6).
Если
,
то система является либо несовместной
(неопределенной) или имеет бесчисленное
множество решений.
Решить систему по формулам Крамера:
1.2.2. Решение систем линейных алгебраических уравнений матричным способом.
Пусть даны матрицы
,
,
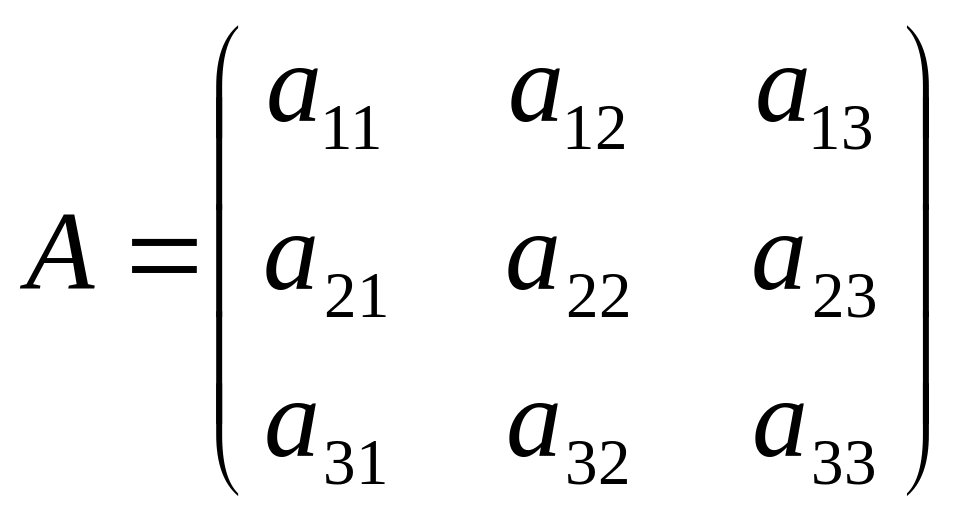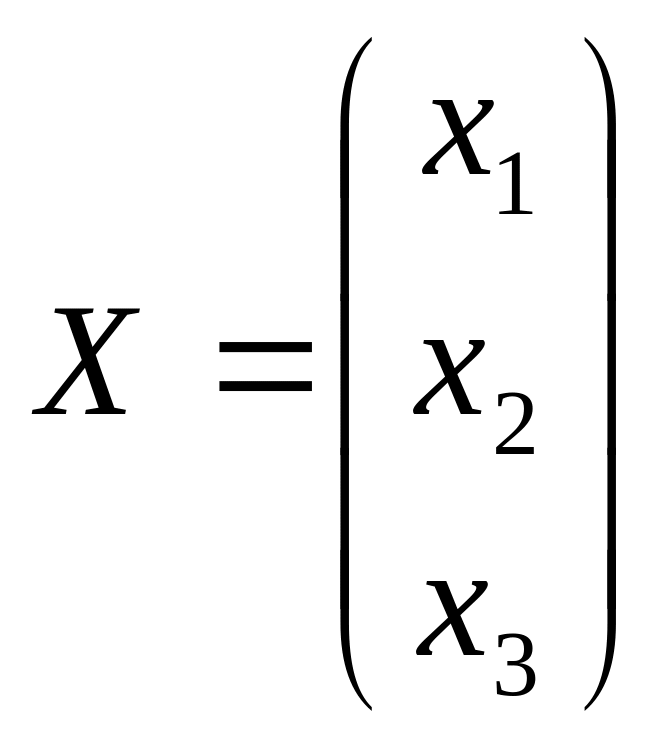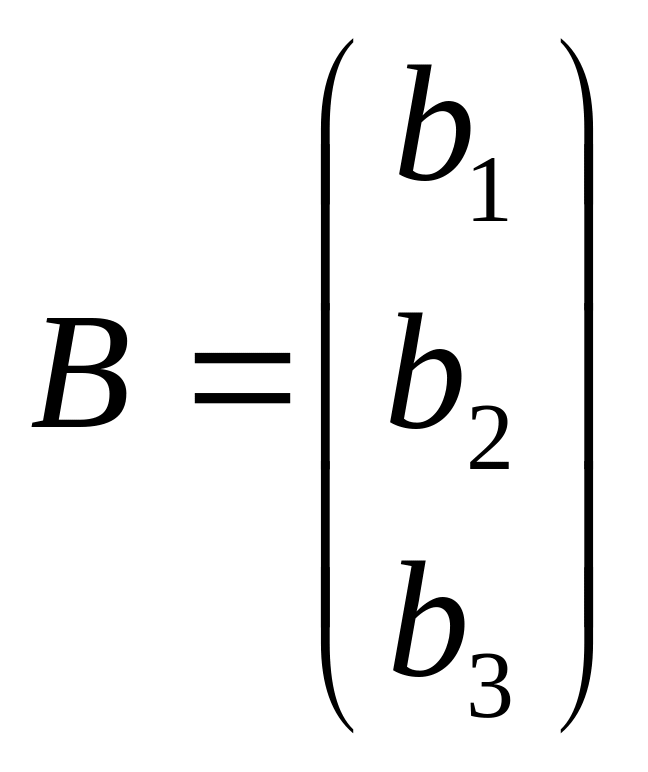
Тогда система линейных уравнений (5) может быть записана в матричном виде:
|
(7) |
Допустим
,
тогда для нее существует обратная
матрица
.
Умножим равенство (7) на
слева:
,
т.к.
,
то имеем матричное решение системы
линейных уравнений (5):
.
Решим матричным методом следующую систему:
Матрицу, обратную к матрице, составленной из коэффициентов системы находим, см. п. 1.1.7.
Самостоятельно решить матричным способом следующую систему:
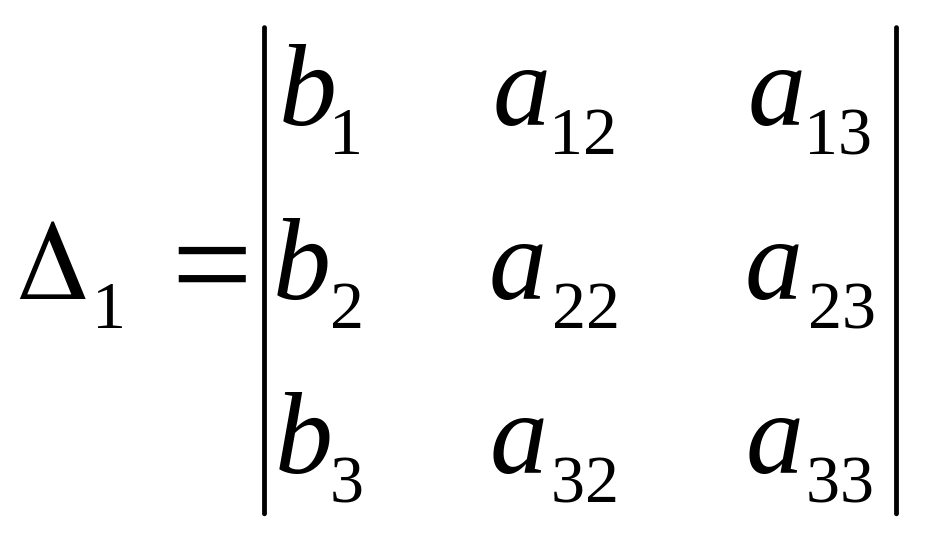