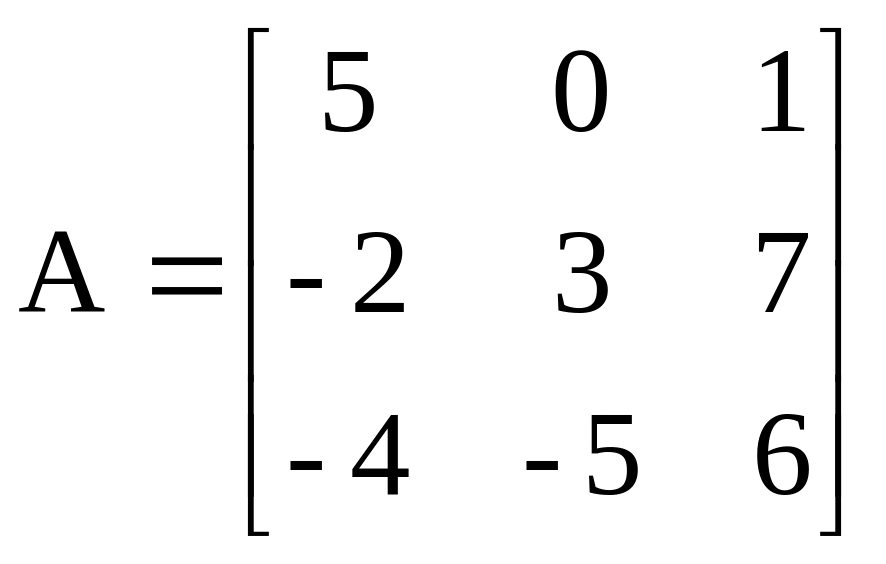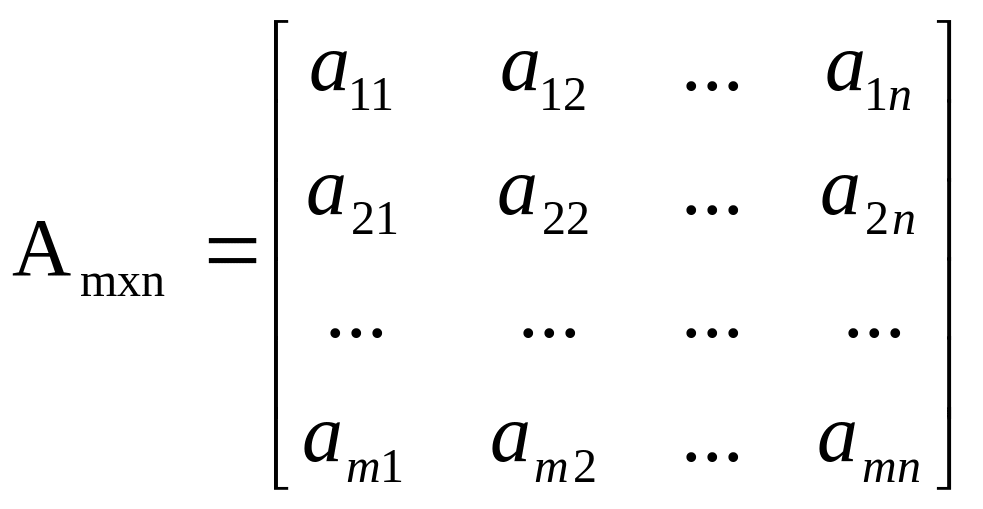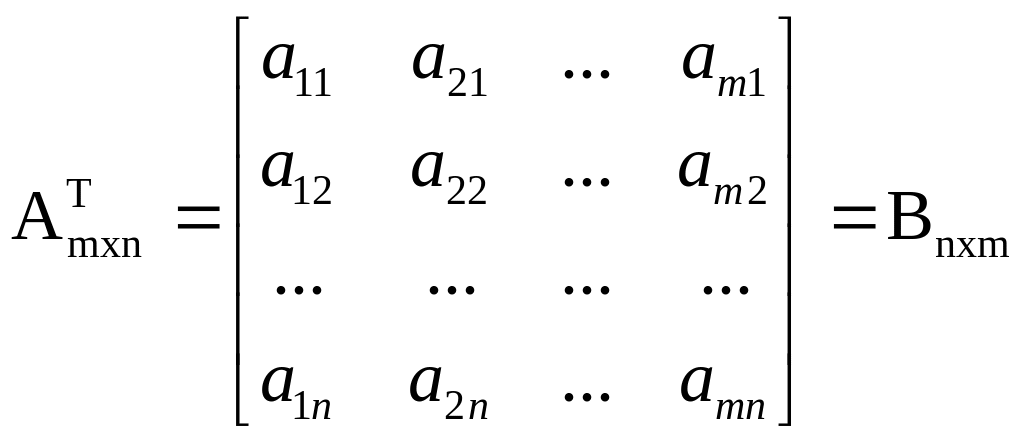Фгбоу впо Кубанский государственный аграрный университет Анапский филиал Рабочая тетрадь по математике

Элементы линейной алгебры и комплексные числа

Элементы векторной алгебры и аналитической геометрии

Введение в математический анализ

Анапа 2012

Анапа 2012 1

2

1.1. Матрицы и определители 4

1.1.1. Матрицы, основные определения 4

Матрицы обозначаются большими буквами A, B, C, … или А_mxn, B_kxl,… 4

1.1.2. Определители второго и третьего порядка. Их свойства. 5

1.1.3 Алгебраические дополнения и миноры. 7

1.1.4. Вычисление определителя разложением по элементам строки (столбца). 7

1.1.5. Понятие об определителе n-го порядка. 8

1.1.6. Алгебра матриц: сложение, умножение на число, произведение матриц. 8

1.1.7. Обратная матрица. 9

1.1.8 Ранг матрицы 10

1.2. Системы линейных уравнений. 10

1.2.1. Решение систем линейных алгебраических уравнений по формулам Крамера. 11

1.2.2. Решение систем линейных алгебраических уравнений матричным способом. 11

1.2.3 Решение систем линейных алгебраических уравнений методом исключения неизвестных (метод Гаусса). 12

1.2.4 Однородная система 13

2. Комплексные числа 16

2.1 Комплексные числа, их геометрическое толкование. Модуль и аргумент комплексного числа. 16

2.2 Алгебраическая и тригонометрическая форма записи комплексных чисел. Показательная форма записи комплексных чисел (формула Эйлера). 17

2.3 Алгебраические действия с комплексными числами. 18

2.4 Полярная система координат. Ее связь с декартовой системой координат. 20

Задачи для самостоятельного решения. 20

1. Элементы линейной алгебры

1.1. Матрицы и определители

1.1.1. Матрицы, основные определения

 Прямоугольная таблица из mxn действительных чисел (или символов), расположенных в m строках и n столбцах называется матрицей.

Матрицы обозначаются большими буквами A, B, C, … или А_mxn, B_kxl,…

	(1)

Числа _ij (i=1,2,…,m; j=1,2,…,n) называются элементами матрицы.

 Запишите матрицу С размера 3x2 в общем виде:

 Если в матрице (1) строки заменить соответствующими столбцами, то получим транспонированную матрицу,

	(2)

 Запишите матрицу C^T из предыдущего примера и :

 Повторное транспонирование приводит к исходной матрице, то есть A^T=B; B^T=A.

 Если в равенстве (1) m=n, то матрица называется квадратной матрицей n-го порядка.

Элементы — образуют главную диагональ квадратной матрицы, а элементы — побочную диагональ.

 Квадратная матрица, у которой все элементы главной диагонали равны 1, а остальные равны нулю называется единичной матрицей.

 Запишите в общем виде квадратную матрицу третьего порядка и единичную матрицу второго порядка.

 Матрица, у которой все элементы, расположенные под главной диагональю, равны нулю называется верхней треугольной матрицей.

 Запишите верхне-треугольную матрицу и нижне-треугольную для матрицы: