См. Также

• Квантование (обработка сигналов)

• Дискретизация

• Covox

• Модем

• Цифровой вычислительный синтезатор

Литература

• Жан М. Рабаи, Ананта Чандракасан, Боривож Николич. Цифровые интегральные схемы. Методология проектирования = Digital Integrated Circuits. — 2-е изд. — М.: Вильямс, 2007. — 912 с. — ISBN 0-13-090996-3

• Mingliang Liu. Demystifying Switched-Capacitor Circuits. ISBN 0-75-067907-7.

• Phillip E. Allen, Douglas R. Holberg. CMOS Analog Circuit Design. ISBN 0-19-511644-5.

1.doc

ЛАБОРАТОРНАЯ РАБОТА № 14 АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ 1. Общие сведения Процесс аналого-цифрового преобразования содержит две операции: дискретизацию и квантование, поэтому АЦП в общем случае изображается структурной схемой рис.5. Дискретизатор выполняет операцию выделения из бесконечного числа значений аналогового сигнала U_вх отдельных мгновенных уровней – выборок U_д, моменты отсчета которых во времени задаются короткими стробирующими импульсами U_стр. 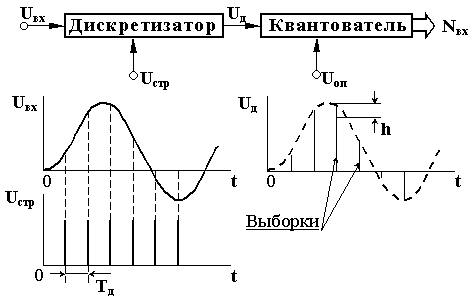Рис.1. Основные операции АЦ – преобразования, N_вх – цифровой эквивалент (код) выборки Дискретизацию быстро изменяющихся сигналов обычно осуществляют устройствами выборки-хранения, а для медленных сигналов она может выполняться во время второй основной операции аналого-цифрового преобразования – квантовании сигнала по уровню. Квантователь АЦП осуществляет оцифровывание, то есть подсчет целого числа квантов, содержащихся в аналоговой выборке. При этом квант АЦП равен h=U_оп/N_мах=U_оп/2^m. В результате квантования получается цифровой эквивалент выборки входного сигнала N_вх. Как известно [2], операция дискретизации, если она выполняется в соответствии с теоремой В.А. Котельникова, не вносит погрешности в сигнал, восстановленный по полученным выборкам. Однако операция квантования всегда сопровождается погрешностью квантования d_кв, поскольку она сопряжена с отбрасыванием части аналоговой выборки (меньшей, чем квант h). 2. Статистическая погрешность квантования АЦП На пис.6,б представлена амплитудная характеристика (АХ) идеального АЦП. Получена АХ путем восстановления кодов АЦП с помощью идеального ЦАП не вносящего собственных погрешностей (рис.6,а). Амплитудная характеристика идеального АЦП – ступенчатая кривая, причем линия, соединяющая середины всех ступеней с началом координат – прямая 1. 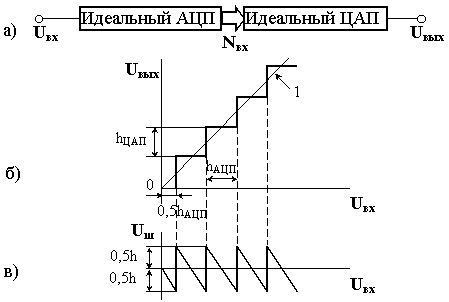Рис.2. АХ идеального АЦП Из АХ АЦП следует, что процесс аналого-цифрового преобразования сопровождается так называемыми шумами квантования U_ш вида рис.6в. Если сложить геометрически АХ АЦП и U_ш, то получим прямую 1, характерную для устройства без погрешностей квантования. Известно [1], что действующее значение шумов квантования Ū_ш=h_ацп/12^1/2=U_оп/12^1/2_*2^m, (5) где m – число разрядов АЦП. Относительная погрешность квантования входного сигнала d_кв=U_ш/U_с, (6) где U_с – действующее напряжение сигнала. Для синусоидального сигнала с максимальной амплитудой U_м=U_оп/2 d_кв составит d_кв=(U_оп/12^1/2_*2^m)/( U_m/2^1/2)=1/6^1/2_*2^m-1. (7) Из (7) следует, что чем больше разрядов m имеет АЦП, тем меньше его относительная погрешность квантования. Следует отметить, что погрешность квантования, определяемая выражением (7), является минимальной. На практике погрешность аналого-цифрового преобразования возрастает за счет деформации АХ АЦП, которая, как и у ЦАП, имеет аддитивную, мультипликативную, дифференциальную и интегральную составляющие (см. рис.3). 3. Методы аналого-цифрового преобразования В аналого-цифровой технике известны три основных метода квантования аналогового сигнала: метода единичных приращений, метод поразрядного уравновешивания и метод считывания. Сравнительные параметры этих методов показаны в таблице 1. Таблица 1. Сравнительные параметры аналого-цифрового преобразования.

Метод АЦП	Число шагов до получения цифрового кода Nвх	Число источников опорного напряжения Uоп	Примечание
Единичных приращений	Nвх	1	Простой, медленный
Поразрядного уравновешивания	M	m	Умеренное быстродействие и аппаратурные затраты
Параллельный	1	2m-1	Быстрый, большие аппаратурные затраты

На практике АЦП строятся также путем комбинации перечисленных выше методов. 4. АЦП единичных приращений и поразрядного уравновешивания Типовая структурная схема АЦП, отражающая методы единичных приращений и поразрядного уравновешивания показана на рис.7. Преобразователи содержат следующие узлы: сравнивающее устройства – компаратор К, управляемый источник опорных напряжений – в данном случае это ЦАП, память двоичных чисел (в качестве ее может быть использован, например, счетчик), генератор тактовых импульсов ГТИ и устройство управления УУ. 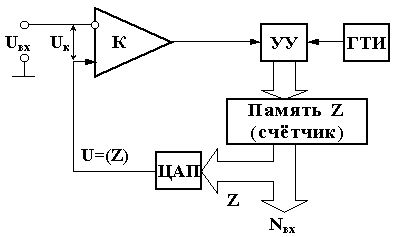Рис.3. Структурная схема АЦП единичных приращений и поразрядного уравновешивания Устройство управления стремится максимально приблизить напряжение ЦАП U(Z) к U_вх, и когда разность напряжений между входами компаратора U_к становится меньше кванта ЦАП, код Z на входе ЦАП представляет собой цифровой эквивалент выборки входного напряжения U_вх. В зависимости от алгоритма работы УУ в структурной схеме рис.7 может реализовываться либо метод единичных приращений, либо метод поразрядного уравновешивания. 2.4.1. Алгоритм работы АЦП единичных приращений Перед началом преобразования УУ устанавливает нули в двоичных ячейках памяти, причем памятью здесь служит двоичный суммирующий счетчик. Вначале работы АЦП двоичный код Z=0 поступает на ЦАП, который преобразует его в напряжение U(Z)=0 и подает на один из входов компаратора. Компаратор сравнивает входное напряжение АЦП U_вх с этим установленным значением U(Z)=0 и, если U_вх>U(Z), то на его выходе появляется логическая единица, которая через УУ разрешает прохождение первого импульса от ГТИ в счетчик (память). С этого момента компаратор сравнивает U_вх с величиной U(Z)=1h_цап и если U_вх>U(Z), то процесс накопления единичных приращений счетчика продолжается до тех пор, пока U_вх<U(Z) и компаратор установит логический нуль на своем выходе. После этого УУ запретит поступление импульсов ГТИ в суммирующий счетчик, который до начала следующего преобразования будет хранить код двоичного числа Z=N_вх, пропорциональный U_вх с точностью до кванта h_цап. Как следует из алгоритма АЦП единичных приращений квант АЦП и его разрядность зависят от кванта и разрядности входящего в него ЦАП, а время преобразования зависит от быстродействия ЦАП и от величины входного напряжения U_вх – оно тем больше, чем больше U_вх. 2.4.2. Алгоритм работы АЦП поразрядного уравновешивания После очистки памяти УУ записывает логическую единицу в старший разряд памяти. При этом выходное напряжение ЦАП U(Z) принимает значение равное половине максимально возможного значения входного напряжения U(Z)=0,5_*U_вх.мах=2^m-1_*h_цап. При U_вх<U(Z) компаратор устанавливается в состояние логического 0 и в старший двоичный разряд Z_m памяти заносится 0 вместо установленной там вначале 1. Если U_вх>U(Z), то в памяти сохраняется Z_m=1 и сохраняется на выходе ЦАП U(Z)=2^m-1_*h_цап. Затем УУ переходит к следующему такту уравновешивания, при котором в память записывается 1 в разряд находящийся ниже старшего Z_m-1, а компаратор сравнивает входное напряжение с разностью U_вх-2^m-1_*h_цап*Z_m. Если эта разность будет меньше величины (2^m-1_*h_цап*Z_m+2^m-2_*h_цап*Z_m-1), то компаратор устанавливается в 0 и вместо Z_m-1=1 записывается в память Z_m-1=0. При U_вх большем указанной выше разности Z_m-1=1 сохраняется в памяти. Этот процесс повторяется до момента уравновешивания младшего разряда Z₀. При этом U(Z) с точностью до кванта h_цап совпадает с U_вх, а в памяти фиксируется цифровой эквивалент выборки N_вх. В целом алгоритм поразрядного уравновешивания АЦП можно записать U_к=U_вх-2^m-1_*h_цап*Z_m-2^m-2_*h_цап*Z_m-1-….-2_*h_цап*Z₁-h_цап*Z₀ < h_цап. (8) Из (8) видно, что процесс уравновешивания выполняется за m тактов и не зависит от величины U_вх, однако погрешность квантования и быстродействие АЦП зависит от параметров ЦАП, входящего в состав АЦП. В настоящее время устройство управления или даже весь АЦП поразрядного уравновешивания выполняется в виде одной интегральной микросхемы (например, 155ИР17 и 1113ПВ1). 5. Параллельные АЦП Принцип работы параллельных АЦП поясним на примере трехразрядного устройства (m=3), показанного на рис.8 [3]. 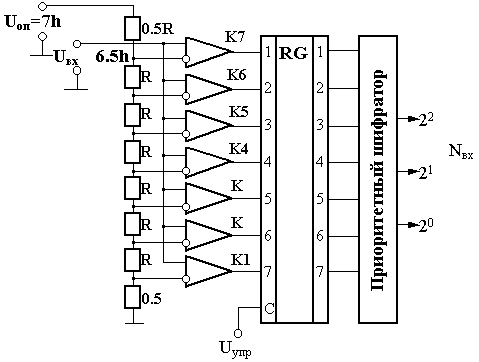Рис.4. Структурная схема трехразрядного параллельного АЦП Преобразователь содержит резистивный делитель (резистивная сетка) из 8-ми резисторов, задающих опорные напряжения на каждом из входов семи компараторов К₁ ….. К₇, на вторые входы которых параллельно поступает входной сигнал U_вх. Выходы компараторов подключены к стробируемому регистру RG, фиксирующему по фронту управляющего сигнала U_упр логические состояния компараторов. Выходные сигналы RG дешифрируются приоритетным шифратором в натуральный двоичный код. Предположим, что U_вх=4h (где, h – квант данного АЦП), тогда входное напряжение превысит опорные напряжения четырех нижних по схеме компараторов. По фронту U_упр в регистр запишется унитарный код 0001111, который в приоритетном шифраторе преобразуется в код 100₂ или 4₁₀. Процесс аналого-цифрового преобразования, таким образом, происходит за один такт. Аналоговое напряжение U_вх как бы считывается в регистр в виде унитарного кода. Параллельные АЦП наиболее быстродействующие устройства и, кроме того, они не требуют применения УВХ для преобразования быстро изменяющихся сигналов. Функцию УВХ в этом АЦП выполняет регистр RG фиксирующий мгновенное состояние не аналоговой величины (как в УВХ), а мгновенные значения унитарных кодов. Однако очевиден и основной недостаток параллельных АЦП: они требуют большого числа радиоэлементов (резисторов, компараторов, триггеров и др.) при увеличении числа разрядов. Так, например 8-ми разрядный АЦП 1107ПВ2 содержит 255 отводов от резистивной сетки, 255 компараторов и триггеров, а также приоритетный шифратор на 255 входов. 6. Основные параметры АЦП 6.1. Статические параметры:

• m – число разрядов, которые определяет максимальное число квантов АЦП N_мах=2^m;

• U_оп – опорное напряжение;

• h – квант АЦП равный h=U_оп/N_мах;

• d_д – статическая дифференциальная нелинейность АХ, определяемая так же, как и у ЦАП.

2.6.2. Динамические параметры АЦП:

• t_пр – время преобразования АЦП, характеризующееся минимальным временем между соседними выборками аналогового сигнала;

• t_а – апертурная неопределенность, которая характеризует динамические искажения АЦП, вносимое им в выходной код за счет конечного времени срабатывания компараторов и неопределенности момента их срабатывания. Апертурная погрешность d_а за счет t_a зависит от скорости изменения входного сигнала dU_вх/dt

d_а=t_a*dU_вх/dt. (9) ^