К.Т.Н., доцент Балашов о.Е.

Методические указания к курсовому проекту по дисциплине «Автоматизация проектирования систем и средств управления»

Вариант 1

Система сопровождения объектов с двумя платформами

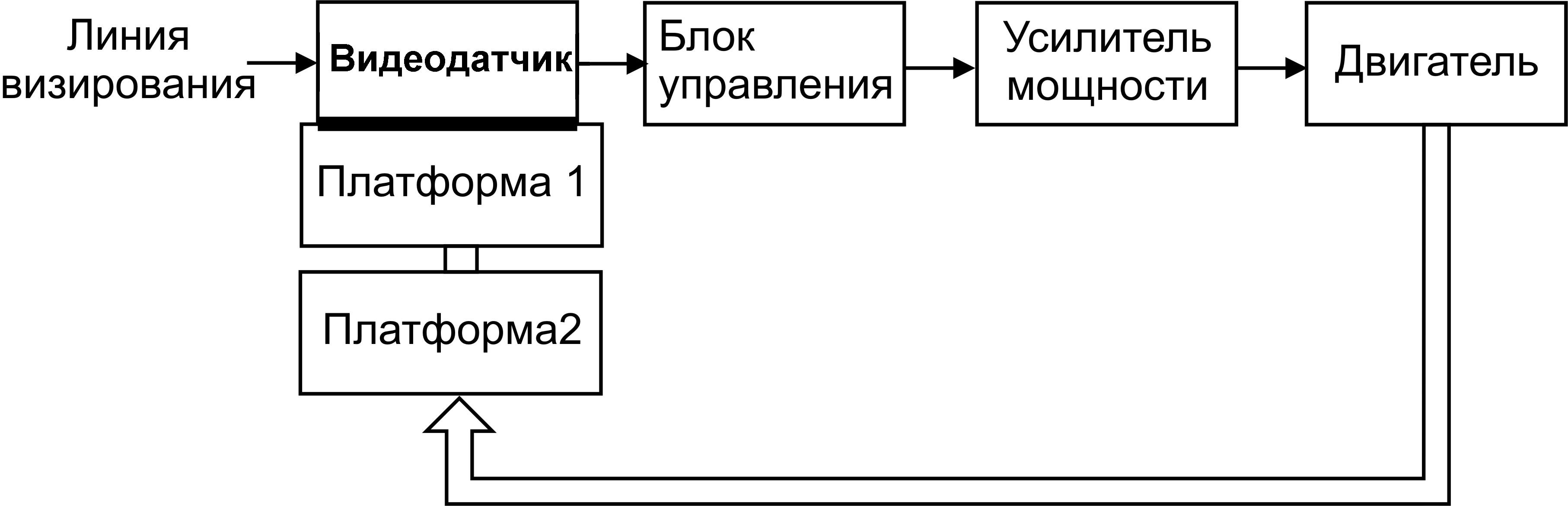
В системах сопровождения (СС) для уменьшения ошибок в переходных режимах и повышения точности совмещения оптической оси видеодатчика (ВД) с направлением на объект могут использоваться исполнительные устройства с двумя опорно-поворотными платформами. Первая платформа обеспечивает быстрый разворот оптической оси ВД в сторону сопровождаемого объекта, однако точность сопровождения объекта при помощи такого исполнительного устройства остается низкой. Поэтому для уменьшения ошибки сопровождения на первой платформе устанавливается вторая для более точного совмещения оптической оси с направлением на объект. Применение двух опорно-поворотных платформ для совмещения оптической оси ВД с направлением на объект уменьшает динамические ошибки сопровождения, обеспечивает возможность отворота первой платформы от направления на объект без перерыва процесса сопровождения.

Рисунок 1 – Структурная схема СС с двумя опорно-поворотными платформами

В некоторых других случаях применение в оптико-механических системах сопровождения объектов двух опорно-поворотных платформами обусловлено конструктивными особенностями.

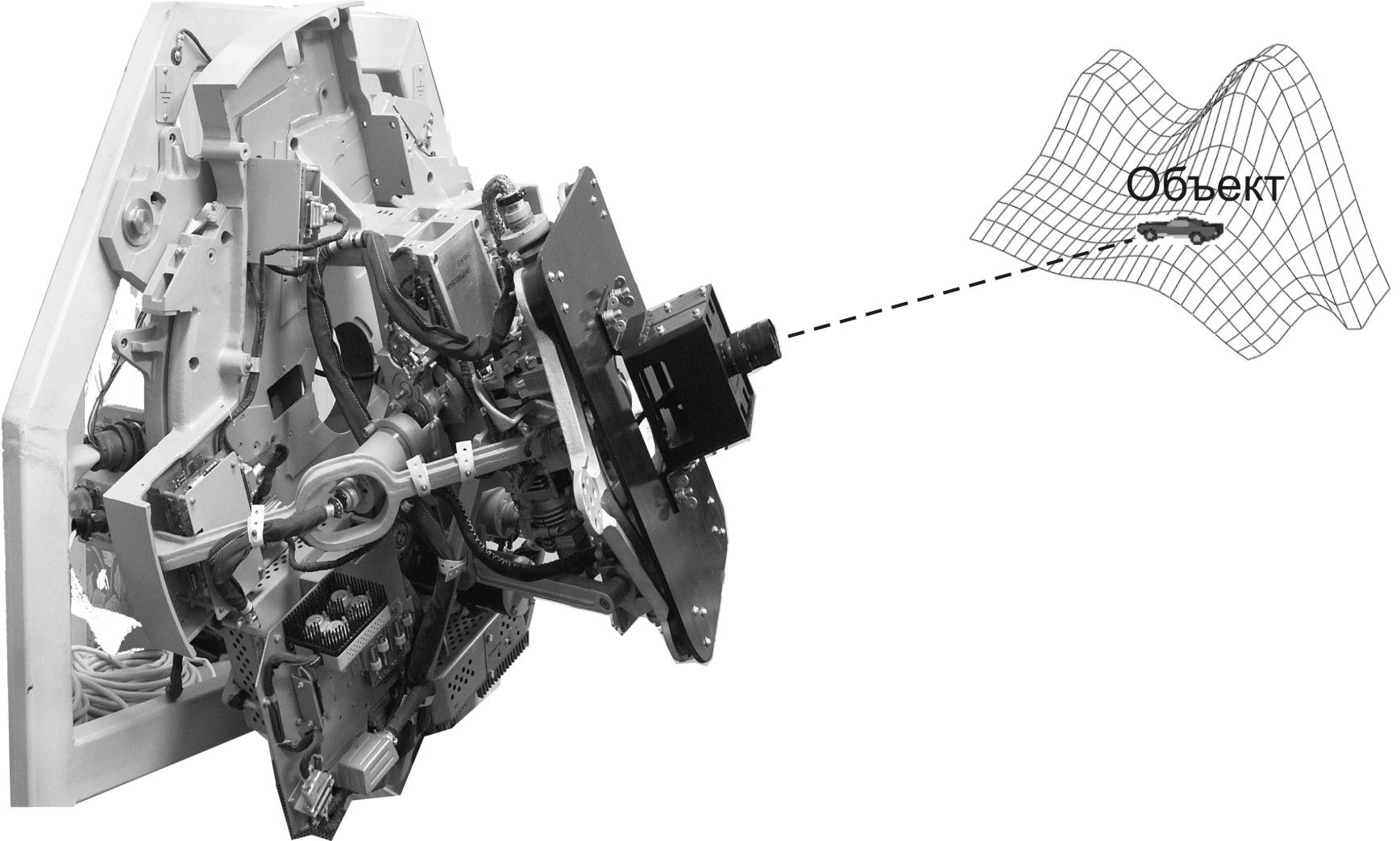
В рассматриваемой задаче сопровождения объектов самоходная установка, на которой размещена опорно-поворотная платформа (платформа 1) представляет некоторый носитель для систем сопровождения (СС) (рисунок Рисунок 2). Опорно-поворотная платформа носителя СС способна вращаться исключительно в горизонтальной плоскости носителя. Оптико-механическая система автоматического сопровождения объектов (система сопровождения), размещенная на опорно-поворотной платформе 1, имеет возможность менять направление оптической оси видеодатчика (ВД) как в горизонтальной плоскости носителя, так и в перпендикулярной ей плоскости.

Рисунок 2 – Схема самоходной установки

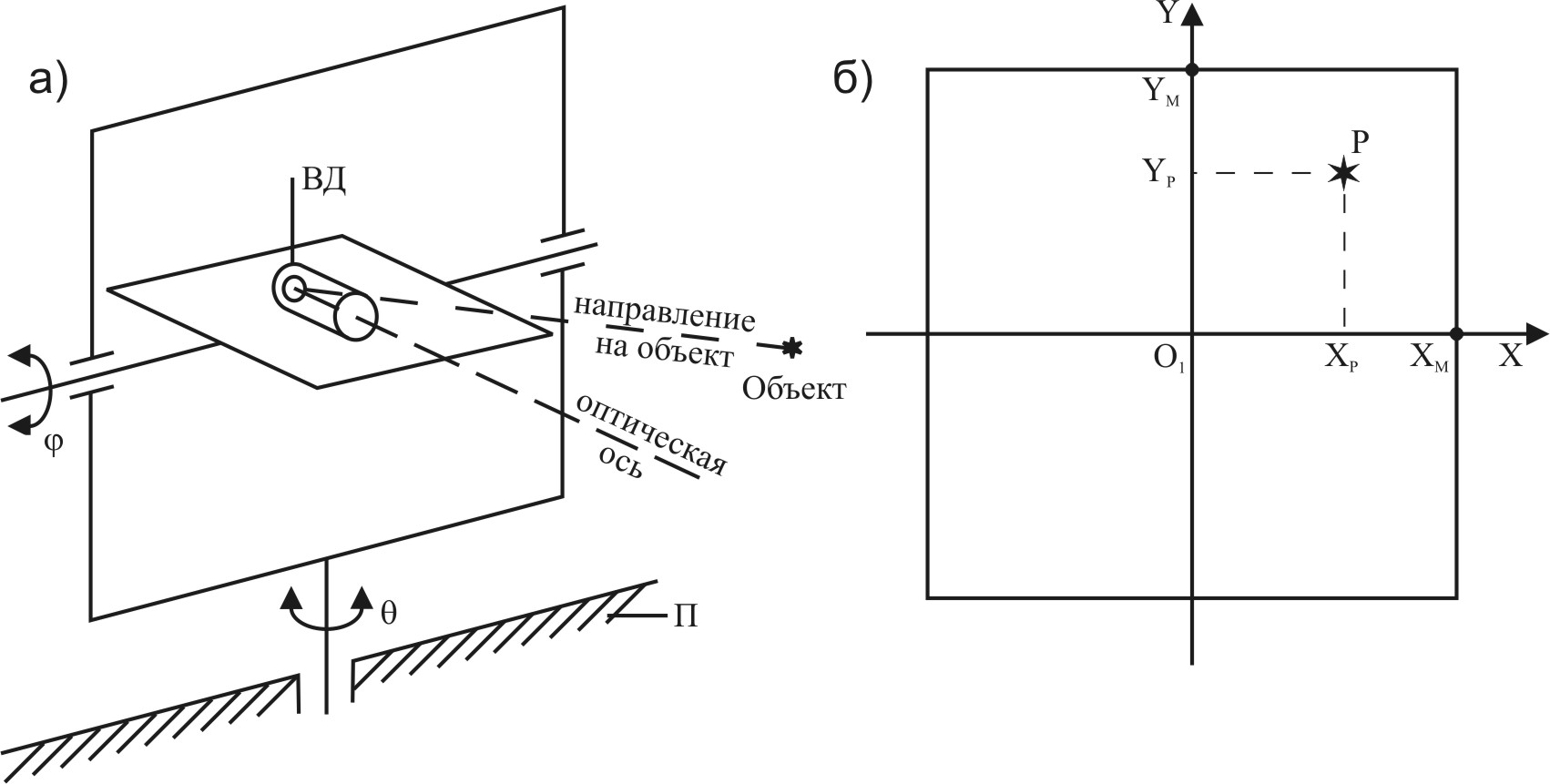
Основной задачей системы сопровождения является непрерывное совмещение оптической оси ВД с направлением на объект, наблюдаемый на изображении, формируемом ВД. Управление положением оптической оси ВД в пространстве осуществляется с помощью двух приводов (рисунок Рисунок 3, а), один из которых изменяет угол поворота внешней рамки двухосной карданной системы относительно платформы П, а другой привод изменяет угол положения внутренней рамки с закрепленным на ней ВД относительно внешней рамки. Направление оптической оси ВД перпендикулярно оси вращения внутренней рамки. На изображении объект (центр изображения объекта) представлен точкой Р (рисунок Рисунок 3, б).

Рисунок 3 – Двухосная карданная система (а) и плоское изображение (б)

Отслеживание положения объекта в пространстве по углу азимута осуществляется двумя платформами (платформой 1 носителя и внешней рамкой карданного подвеса СС), которые включены в азимутальный контур следящей системы таким образом, что в состоянии равновесия системы направление продольной оси платформы 1 и оптической оси ВД совпадают с направлением на отслеживаемый объект. Отслеживание по углу места в системе координат носителя происходит при помощи вращения только внутренней рамки кардана;

Пусть положение объекта в пространстве относительно неподвижно ориентированной системы координат, центр которой совпадает с центром системы координат строительных осей носителя (совпадает с центром носителя), определяется углами и . Углы поворота СС и выдаются соответствующими цифровыми датчиками углов поворота рамок карданного подвеса с частотой дискретизации системы управления (указана в вариантах задания). Угол поворота платформы 1 в горизонтальной плоскости выдается цифровым датчиком углав поворотаплатформы.

Функциональная схема системы сопровождения объектов по углу азимута представлена на рисунке Рисунок 4.

Рисунок 4 – Функциональная схема системы по углу азимута

Функциональная схема системы сопровождения объектов по углу места представлена на рисунке Рисунок 5 .

Рисунок 5 – Функциональная схема системы по углу места

Блок обработки изображения и формирования управления определяет координаты центра изображения объекта и в плоскости изображения каждого видеокадра, формируя при этом сигнал рассогласования, который подается на замкнутый следящий контур СС и сумматор на входе следящего контура платформы 1.

Оптической оси ВД соответствует точка на изображении. Считается известным угловое поле зрения ВД, которому соответствует прямоугольное изображение (рисунок Рисунок 3, б). По измеренным значениям координат объекта , , преобразованным в угловые координаты и , показаниям датчиков углов поворотов рамок кардана , и угла поворота платформы 1 по азимуту на момент получения видеокадра определяется рассогласование между направлением оптической оси системы и направлением на объект. При этом величины и будут представлять рассогласование системы, а и в некоторой принятой системе отсчета можно рассматривать как заданные значения углов, определяющих направление на объект.

Функциональная схема следящего привода представлена на рисунке Рисунок 6.

Рисунок 6 – Функциональная схема следящего привода

Для исследования точностных характеристик системы необходимо знать математическую модель оптико-механической системы. В случае, когда точно не известна внутренняя структура исполнения приводов карданного подвеса, можно получить приближенную передаточную функцию приводов по данным экспериментального исследования. Часто математическую модель объекта определяют по его реакции на детерминированный входной сигнал (обычно по переходной характеристике).

Разработанные в настоящее время методы идентификации систем позволяют, вообще говоря, определить только постоянные коэффициенты линейного дифференциального уравнения, которым предположительно описывается объект исследования. Выявление же полной структуры системы и порядка описывающего ее уравнения вообще невозможно.

Математическая модель приводов скорости оптико-механической системы может быть получена при помощи метода идентификации систем, основывающегося на аппроксимации переходных характеристик.