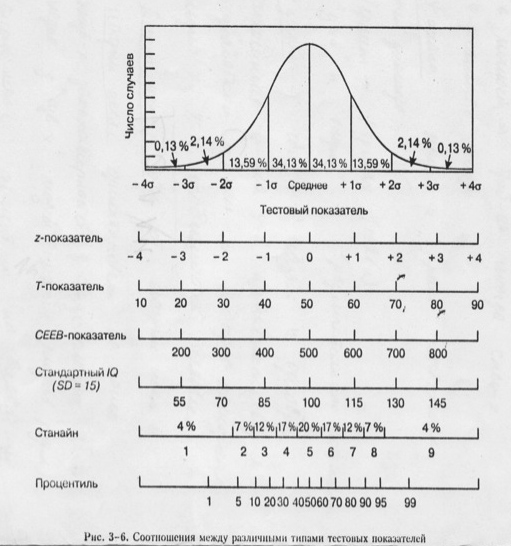
18. Понятие нормы, психодиагностические нормы (возрастные, внутригрупповые, процентили). Стандартизация психодиагностических тестов.

СТАНДАРТИЗАЦИЯ - унификация к единым нормативам процедуры и оценок теста.

Стандартизацию проводят на большой репрезентативной выборке лиц определенного типа, для работы с которыми он предназначен. Эта группа называется выборкой стандартизации. Сам тест выступает в качестве единственного эталона, а в качестве меры измеряемого свойства выступает место балла на кривой распределения.

Стандартизация состоит из:

• нормализации шкал теста

• унификации системы интерпретации результатов.

В психометрике следует различать две формы стандартизации:

1. теста - самой процедуры проведения инструкций, бланков, способа регистрации, условий и т.п. Без стандартизации теста невозможно получить нормативное распределение тестовых баллов и, следовательно, тестовых норм.

2. шкалы - линейное преобразование масштаба нормальной (или искусственно нормализованной) шкалы. В общем случае формула стандартизации выглядит так:

,

где x_i - исходный балл по «сырой» шкале, для которой доказана нор­мальность распределения;

- среднее арифметическое по «сырому» распределению; S - «сырое» стандартное отклонение;

М- математическое ожидание по выбранной стандартной шкале;

σ - стандартное отклонение по стандартной шкале.

Если шкала подвергалась предварительной искусственной норма­лизации интервалов, то формула упрощается:

z_j =σ z_j =M

Стандартизированный показатель (Z- показатель) – это отклонение сырого показателя от среднего нормативного значения, деленное на стандартное отклонение (сигму). Главным недостатком Z-показателя является то, что он может занимать на оси координат как положительное, так и отрицательное значение.

Применение стандартных шкал необходимо для соотнесения ре­зультатов по разным тестам, для построения «диагностических про­филей» по батарее тестов и тому подобных целей.

Стандартизация необходима по нескольким причинам:

1. Когда тест содержит несколько шкал, далеко не всегда эти шкалы включают одинаковое количество заданий, кроме того не все шкалы будут иметь одинаковое среднее арифметическое. Чтобы можно было отобразить эти шкалы на едином графике-профиле, либо просто выяснить их соотношение они должны быть приведены к одной единице измерения, что и производится в процессе стандартизации.

2. Существует множество тестов, измеряющих одно и то же свойство. Для возможности сопоставления результатов этих тестов необходимо перевести результаты их всех в одну и ту же единицу измерения. Это успешно реализовано в разнообразных тестах интеллекта, которые используют IQ как универсальную шкалу. К сожалению, в личностных опросниках такого единогласия фактически нет.

3. Стандартизированные шкалы удобны для анализа. Любой, даже неопытный человек гораздо лучше воспринимает процентиль, чем сырой балл (именно поэтому так популярны процентили), а в профессиональном анализе результатов тестов стандартизация повышает скорость аналитической работы.

4. Тест применяется для сравнения результатов со средним и для определения степени, в которой результаты отклоняются от среднего. Если этих показателей нет, то тест оказывается бессмысленным.

Нормализация

Применяется процентильная шкала. В качестве универсальной меры, пригодной для разных (по своей качественной направленности и количеству пунктов) тестов, используется «процентильная мера». Многие тесты познавательных способностей, а так же некоторые личностные опросники используют нелинейное преобразование при стандартизации полученных сырых значений. Достоинство нелинейного преобразования в том, что нам не нужно задумываться как распределены баллы теста – нормально или нет. Типичной нелинейной шкалой являются процентили, получившие очень широкое распространение в психодиагностике за счет своей наглядности и простоты восприятия.

Процентилъ - процент испытуемых из выборки стандартизации, которые получили равный или более низкий балл, чем балл данного испытуемого. Таким образом, в качестве источника данной меры выступает нормативная выборка (выборка стандартизации), на которой построено нормативное распределение тестовых баллов.

Процентильные шкалы лежат в основе всех традиционных шкал, применяемых в тестологии (Т-баллы MMPI, баллы IQ, стены 16 PF и др.).

Нормальность распределения достигается искусственным подбором пунктов теста с заданными статистическими свойствами.

Подчеркнем, что с точки зрения теории измерений, процентильные шкалы относятся к порядковым шкалам: они дают информацию о том, у кого из испытуемых сильнее выражено измеряемое свойство, но не позволяют говорить о том, во сколько раз сильнее.

В результате нормализации интервалы между исходными сырыми баллами переоцениваются в соответствии с нормальной моделью. В отличие от процентильной шкалы, нормальная шкала придает больший вес (в дифференциации испытуемых) краям распределения: различия между испытуемыми, набравшими 95 и 90 процентилей, оцениваются как более высокие, чем различия между испытуемыми, набравшими 65 и 60 процентилей.

Переход к нормальному распределению создает очень удобные условия для количественных операций с диагностической шкалой: как со шкалой интервалов с ней можно производить операции линейного преобразования (умножение и сложение), можно описывать диагностические нормы в компактной форме (в единицах отклонений), можно применять линейный коэффициент корреляции Пирсона, критерии для проверки статистических гипотез, построенные в применении к нормальному распределению, т. е. весь аппарат традиционной статистики (основанной на нормальном распределении).

Нормализованные шкалы, используемые при стандартизации методик:

• 1)Шкала структуры интеллекта по Амтхауэру:

Z_a = 100 + 10(x–X)/S_x = 100 + 10z

• 2)Шкала Векслера:

IQ = 100 + 15 (x–X)/ S_x = 100 + 15z

• 3)Шкала стенайнов (Гилфорда):

C = 5 + 2(x–X)/ S_x = 5 + 2z

• 4)Шкала школьных оценок:

SN = 3 + (x–X)/ S_x = 3 + z

• 5)Шкала стэнов (Кеттела):

ST = 5,5 + 2(x–X)/ S_x = 5,5 +2z

• 6)Шкала Т-преобразований Мак-Кола:  

Т = 50 + 10 (х–X)/ S_x = 50 + 10z