Вариант 1
1. Вычислить определитель матрицы:
1) 0 2) 2 3) 3 4) 4 5) 5
Решение. Раскладываем определитель по первой строке:
2. Если (
)
− решение системы линейных уравнений
тогда
равно…
1) − 0,5 2) 7,5 3) 0,5 4) − 7,5 5) 0
Решение. Вычитаем из первого уравнения второе:
− 2x = −8 → x = 4
Подставляя x в первое уравнение, находим y:
4 + 2y = − 3 → y = − 3,5 → x – y = 4 – (−3,5) = 7,5
3. Если даны две координаты вектора x = 4, y = − 12 и длина его равна 13, то третья координата вектора равна…
1) 3 2) − 3 3) ± 3 4) 0 5) 4
Решение.
Длина вектора находится по формуле
.
Подставляем данные:
.
4. Прямая проходит через точки О(0;0) и В(5;10). Тогда ее угловой коэффициент равен…
1) 3 2) − 5 3) 2 4) 5 5) – 2
Решение. Используем уравнение прямой с угловым коэффициентом y = kx + b, где угловым коэффициентом является k. Если прямая проходит через точку О(0;0), то ее координаты удовлетворяют уравнению прямой: 0 = k∙ 0 + b → b = 0. Аналогично поступаем с точкой В(5;10): 10 = k∙5 → k = 2.
5. Вычислить
1) 0 2)
−5 3)
4) 0,5 5) 2
Решение.
Имеем неопределенность вида
.
Выносим старшие степени x
в числителе и знаменателе дроби:
.
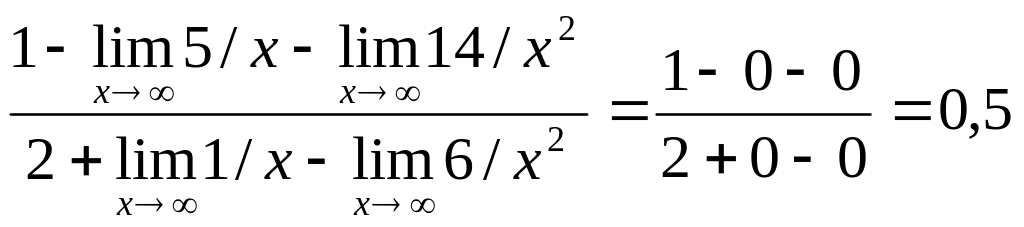6. Если y
=
,
то y’
= …
1)
2)
+ 1 3)
4)
5)
Решение.
Раскроем скобки: y
=
.
Производная от суммы функций равна
сумме производных от этих функций:
.
Вариант 2
1. Вычислить определитель матрицы:
1) 2x + 4 2) 3x − 1 3) 3x 4) − 3x + 1 5) 3x + 1
2. Если (
)
− решение системы линейных уравнений
тогда
равно…
1) 3,5 2) 2,5 3) 4,5 4) − 3,5 5) 1,5
3. Угол между
векторами
=
+
2
+ 3
и
= 6
+ 4
− 2
равен…
1) arccos 2
2) arccos
3) arccos
4) arccos
5) arccos
4. Прямая проходит через точки О(0;0) и В(5; − 15). Тогда ее угловой коэффициент равен…
1) − 3 2) −5 3) 3 4) 5 5) 0
5. Вычислить
1) 0 2) − 3 3) 3 4) 0,5 5) − 0,7
6. Если y
=
,
то y’
= …
1)
2)
3)
4) 0 5) –
Вариант 3
1. Вычислить определитель матрицы:
1) sin 2x 2) cos 2x 3) − 1 4) 1 5) 0
2. Если ( ) − решение системы линейных уравнений
тогда равно…
1) 1,5 2) 2 3) 0,5 4) 2,5 5) − 2
3. Векторы m − 3 + 2 и + 2 − m взаимно перпендикулярны при m равном
1) 5 2) − 5 3) 0 4) 6 5) − 6
4. Прямая проходит через точки О(0;0) и В(2;4). Тогда ее угловой коэффициент равен…
1) 1 2) 2 3) 3 4) 4 5) 5
5. Вычислить
1) − 1,4
2)
3) 0 4)
5) 0,5
6. Если y
=
,
то y’
= …
1)
(1
+ xln10) 2)
ln10
3) lnx(1 + x) 4) (x − 1)
5) (x + 1)
Вариант 4
1. Вычислить определитель матрицы:
1) − 3 2) 3 3) − 2 4) 2 5) 0
2. Если (
)
− решение системы линейных уравнений
тогда
равно…
1) 15 2) 20 3) 13 4) − 6,5 5) 0
3. Даны вершины треугольника A(1; 2; 1), B(3; −1; 7), C(7; 4; −2). Является ли этот треугольник равнобедренным?
1) Нет 2) Да, AB = BC 3) Да, AB = AC 4) Да, BC = AC 5) Да, AB = BC = AC
4. Прямая проходит через точки О(0;0) и В(3; − 9). Тогда ее угловой коэффициент равен…
1) − 3 2) 6 3) − 6 4) 0 5) 3
5. Вычислить
1) 2) − 3 3) 0,75 4) 0,8 5) − 4
6. Если y
=
,
то y’
= …