2.4 Физическая картина и особенности теплообмена при протекании процессов плавления и затвердевания

Плавление и затвердевание представляют собой фазовые пере­ходы вещества с изменением его агрегатного состояния при пре­вращении твердого тела в жидкость и наоборот. Эти превраще­ния сопровождаются тепловым эффектом и скачкообразным из­менением плотности.

Процессы плавления и затвердевания являются неотъемлемой частью большинства технологических операций по производству и переработке различных металлов и сплавов. Получение металлов из руд, рафинирование сплавов, ввод в сплавы легирующих доба­вок с целью желаемого изменения их свойств, кристаллизация слитков и отливок — вот далеко неполный перечень технологи­ческих процессов, в ходе которых имеют место плавление и за­твердевание. Широкое разнообразие названных задач предопреде­ляет и различие условий, в которых протекают эти процессы. Плавление осуществляют в самых различных металлургических печах, а также в ковшах при внепечной обработке металла. За­твердевание расплава происходит в изложницах и литейных фор­мах, а также на любых твердых поверхностях, через которые от­водится тепло от вступающего с ними в контакт расплава (стенки ковшей, водоохлаждаемые элементы конструкций печей и т.п.).

Несмотря на разнообразие этих условий, процессам плавления и затвердевания, как физическим явлениям, присущи некоторые общие закономерности. К ним относится, прежде всего, наличие движущейся поверхности раздела твердой и жидкой фаз. Эту по­верхность называют фронтом фазового превращения. Для плос­кого фронта меняющееся во времени положение его координаты ( , м) определяет скорость плавления или

затвердевания ( , м/с). Температура фронта фазового превращения чис­того кристаллического вещества имеет определенное постоянное значение. Эта температура, называемая точкой фазового превра­щения (Т_пр), служит одной из теплофизических характеристик ве­щества.

Другой характеристикой, оказывающей существенное влияние на скорость перемещения фронта фазового превращения, являет­ся тепловой эффект процесса, называемый удельной (скрытой) теплотой фазового превращения. Эта величина (L, Дж/кг) равна количеству тепла, поглощаемого при плавлении единицы массы твердого вещества или выделяющегося при затвердевании едини­цы массы расплава. В случае чистого кристаллического вещества поглощение или выделение теплоты фазового перехода происхо­дит на фронте фазового превращения.

При плавлении и затвердевании многокомпонентных веществ или сплавов тепловой эффект фазового превращения реализуется не при определенной температуре, а в некотором интервале тем­ператур. Для сплавов этот интервал температур соответствует диа­пазону между линиями ликвидус и солидус. Поверхность фронта превращается при этом в двухфазную область, где одновременно существуют твердая и жидкая фазы. Эта область имеет некото­рую толщину и характеризуется тем, что температура одной ее поверхности определяется линией солидус, а другой — линией ликвидус.

При решении многих технических задач часто используют допущение о том, что процесс плавления многокомпонентного ве­щества протекает при некоторой постоянной температуре, за ко­торую принимают обычно температуру линии ликвидус. Такое до­пущение существенно упрощает математическое описание процесса, и в случае, когда разность температур ликвидус и со­лидус невелика, этот подход является приемлемым, позволяя по­лучать достоверные результаты по скорости движения границы раздела фаз.

Тепловые процессы при плавлении и затвердевании. В общем случае направление и скорость перемещения меж­фазной поверхности (при заданных значениях ρ и L) зависит от соотношения плотностей подводимого к ней q, Вт/м², и отводи­мого от нее q', Вт/м², тепловых потоков.

При плавлении тепловой поток подводится от внешнего ис­точника тепла (электрическая дуга, раскаленные продукты сгора­ния топлива и т. п.), а отводится внутрь твердого остатка плавя­щегося тела.

При затвердевании тепло передается от расплава к фронту фа­зового превращения и далее через слой затвердевшего расплава к некоторой твердой поверхности, через которую оно и отводится из системы.

Разность между плотностями подводимого и отводимого теп­ловых потоков служит движущей силой процесса фазового пре­вращения. При q = q' никакого фазового превращения не проис­ходит, и, соответственно, скорость перемещения межфазной по­верхности равна нулю. Если q > q', на границе раздела фаз возникает избыток тепла, расходуемый на плавление, и эта гра­ница перемещается внутрь твердой фазы. В случае q < q' дефицит тепла на фронте фазового превращения, восполняемый выделе­нием тепла фазового превращения, обусловливает перемещение границы раздела внутрь жидкой фазы, т.е. происходит ее затвер­девание. Рис. 24.1 наглядно иллюстрирует три эти возможные ситуации, показывая соответствующие направления вектора ско­рости движения межфазной поверхности.

Для количественной оценки направления и скорости движе­ния границы раздела фаз запишем выражение закона сохранения энергии на ней, называемое условием Стефана:

(2.12)

где — плотность твердой фазы, кг/м³. Здесь разность имеет смысл плотности результирующего теплового потока на границе раздела фаз. Когда эта разность положительна, то и ве­личина имеет положительный знак, а направление век­тора скорости перемещения фронта такого, что имеет место затвердевание расплава с уменьшением объема жидкой фазы. При отрицательном значении разности величина также отрицательна, и направление вектора скорости оказывается противопо­ложным, т.е. протекает процесс плавления, сопровождающийся сокращением объема твердой фазы и увеличением объема расплава.

Таким образом, как это следует из соотношения (2.12), на фронте фазового превращения плотность теплового потока скач­кообразно изменяется, тогда как температурное поле в обеих фазах остается непрерывным, будучи связанным значением тем­пературы фазового превращения на границе раздела фаз.

На картину теплообмена при плавлении и затвердевании су­щественное влияние оказывают особенности предшествующих процессов (нагрев твердого тела перед плавлением и охлаждение расплава перед началом его затвердевания). При этом возможны предельные случаи, когда температурное поле одной из фаз рав­номерно, т.е. в ней отсутствует градиент температуры.

Так, охлаждение расплава может протекать таким образом, что к моменту достижения температуры фазового превращения весь его объем имеет постоянную температуру, равную Т_пр. В этом случае плотность теплового потока, подводимого к фронту фазо­вого превращения от расплава, равна нулю (q = 0), и скорость затвердевания обусловлена только интенсивностью отвода тепла от фронта фазового превращения, т. е. величиной q'. При нали­чии перегрева расплава (при q > 0) скорость затвердевания умень­шается в тем большей степени, чем выше градиент температуры в жидкой фазе у межфазной поверхности и чем, следовательно, больше величина q.

Что касается плавления, то ему всегда предшествует нагрев твердого тела вплоть до достижения его поверхностью температуры фазового превращения. При этом нагрев тела может протекать по закономерностям, свойственным либо термически тонким, либо термически массивным телам. В первом случае после достижения точки фазового превращения начинается плавление твердого тела, равномерно прогретого до температуры T_пр. Тогда плотность теплового потока q' отводимо­го от границы раздела фаз, равна нулю, и все тепло, подводимое к этой границе, затрачивается только на плавление, скорость ко­торого является максимально возможной при прочих равных ус­ловиях. При постоянстве плотности теплового потока q, подводи­мого к границе раздела фаз, как это следует из условия Стефана (2.12), скорость плавления термически тонкого тела постоянна.

Если предшествующий плавлению нагрев протекал в термичес­ки массивном теле, то скорость его плавления будет тем ниже, чем больше градиент температуры в твердом остатке у границы раздела фаз. По мере сокращения объема твердого остатка и его прогрева градиент температуры внутри тела уменьшается, и, со­ответственно, снижается плотность отводимого внутрь него теп­лового потока q'. Это (при постоянстве плотности подводимого к границе раздела фаз теплового потока q) вызывает рост скорости плавления вплоть до достижения величины скорости плавления термически тонкого тела.

При анализе процесса плавления следует учитывать влияние еще одного фактора, оказывающего существенное влияние на скорость процесса. Этот фактор характеризует поведение образу­ющейся жидкой фазы, которая может либо накапливаться на по­верхности твердого остатка (например, на слое шихты, лежащей на поду плавильной печи), либо быстро стекать с нее (например, с плавящегося торца расходуемого электрода).

В первом случае тепло от внешнего источника передается к фронту плавления через слой образующегося расплава, имеющий меняющуюся во времени толщину и представляющий, таким об­разом, переменное тепловое сопротивление. При неподвижности этого расплава (что может иметь место в случае его расположе­ния на горизонтальной поверхности и подводе тепла сверху от внешнего источника) конвективные потоки

не получают разви­тия, и тепло передается к фронту плавления через слой жидкой фазы посредством молекулярной теплопроводности. Во всех слу­чаях обязательным условием протекания процесса плавления под слоем расплава является перегрев жидкой фазы, обеспечивающий некоторый температурный напор и, следовательно, тепловой по­ток к фронту фазового превращения. Чем больше плотность это­го потока, тем выше скорость плавления.

Очевидно, что при прочих равных условиях скорость плавле­ния с удалением расплава выше, чем в случае его накопления на поверхности плавящегося тела, поскольку тепло не расходуется на перегрев образующегося расплава, а поступает от внешнего ис­точника непосредственно к фронту плавления. Внешний тепло­вой поток может формироваться за счет переноса тепла конвек­цией или излучением, либо при совместном протекании этих процессов. При этом если температура источника тепла (грею­щей среды) постоянна, то благодаря Неизменности температуры на поверхности плавящегося тела при удалении с него расплава плотность подводимого теплового потока q сохраняет постоянное значение.

Еще один вариант условий перехода твердых тел в жидкое состояние возникает при осуществлении технологий, связанных с погружением этих тел в расплавы (например, кусков лигатур, ферросплавов и раскислителей в жидкую сталь). В этом случае собственно плавлению погружаемого твердого тела предшествует период его нагрева, отличающийся тем, что на поверхности тела возникает (и затем оплавляется) слой затвердевшего расплава, ча­сто именуемый «корочкой» или «гарнисажем». Образование ко­рочки обусловлено тем, что сразу после ввода твердого тела (обычно с комнатной начальной температурой) в перегретый до температуры Т_р расплав в поверхностном слое тела возникает большой градиент температуры. При этом величина плотности теплового потока q' отводимого через корочку внутрь тела, пре­вышает плотность теплового потока q' подводимого к ней от расплава, и значение в соотношении (2.12) становится положительным, что свидетельствует о затвердевании расплава и увеличении толщины корочки. Следует иметь в виду, что темпе­ратура на внешней поверхности затвердевшего слоя равна темпе­ратуре фазового превращения расплава, вследствие чего плотность подводимого от расплава к корочке теплового потока q постоян­на (при условии Т= const). По мере прогрева твердого тела гра­диент температуры в нем уменьшается, и, следовательно, умень­шается величина плотности теплового потока q'. В момент вре­мени, для которого плотности отводимого и подводимого тепловых потоков становятся равными (q' - q), величина обращается в нуль, и толщина корочки достигает своего макси­мального значения.

Затем, при q' < q, начинается оплавление затвердевшего слоя, которое завершается его полным исчезнове­нием с поверхности тела, температура которой в этот момент становится равной температуре фазового превращения расплава. Описанный начальный этап процесса нагрева твердого тела при его погружении в расплав часто называют «тепловым периодом». После его окончания начинается непосредственное взаимодействие твердого тела с расплавом, сопровождающееся плавлением тела. Последующие за тепловым периодом стадии перехода твердого тела в расплав протекают существенно по разному в зависимости от соотношения температур фазового превращения твердого тела (Т_пр) и расплава ( ). Возможны три ситуации:

-Т_пр = (плавление тела такого же состава, как и рас­плав);

-Т_пр> (плавление относительно тугоплавкого тела);

-Т_пр < (плавление относительно легкоплавкого тела).

В первом случае после окончания теплового периода сразу на­чинается плавление погруженного в расплав твердого тела, про­текающее в соответствии со всеми рассмотренными выше зако­номерностями.

Во втором случае, когда к моменту окончания теплового пери­ода на поверхности погруженного тела достигается температура фа­зового превращения вещества расплава , его плавление начать­ся еще не может, так как необходимо некоторое время для того, чтобы поверхность твердого тела нагрелась до температуры Т_пр. Если температура расплава выше температуры плавления твердого тела, т.е. Т_р > Т_пр, то после достижения на поверхности темпера­туры Т_пр начинается плавление при q = const.

Если же температура расплава ниже точки плавления твердого тела (например, при вводе тугоплавких ферросплавов в жидкую сталь), переход твердого тела в расплав возможен посредством растворения. В случае наличия в расплаве каких-либо примесей, понижающих температуру плавления до уровня Т_пр< Т_р (напри­мер, углерода при плавлении стали в жидком чугуне), благодаря их диффузии из расплава в поверхностные слои твердого тела возникает тепловой поток к фронту фазового превращения, дос­таточный для плавления. Такой механизм перехода погруженного в расплав твердого тела в жидкое состояние получил название диффузионного плавления.

В третьем случае, например, при плавлении легкоплавких до­бавок в жидкой стали, еще до исчезновения корочки затвердев­шего расплава под ней начинается плавление твердого тела, и об­разуется слой жидкой фазы. Рассматриваемая система на этой стадии отличается наличием двух фронтов фазового превращения: одного на границе раздела

корочки и расплава, а другого - на границе между твердым остатком погруженного тела и образовав­шейся при его плавлении жидкой фазой, заключенной под еще существующей корочкой. В зависимости от количественного со­отношения температур Т_пр и , а также от температуры рас­плава Т_р и интенсивности теплоотдачи от него, момент начала плавления твердого тела под корочкой затвердевшего расплава может соответствовать или этапу ее нарастания, или оплавления. Эти же факторы предопределяют картину завершения плавления твердого тела: либо оно полностью расплавляется еще под ко­рочкой, либо существование корочки прекращается, когда плав­ление твердого остатка еще не завершилось.

Общая постановка задач плавления и затвердевания. Возможность решения задач плавления и затвердевания имеет большое практическое значение, поскольку она открывает пути совершенствования широкого круга технологических процессов в металлургии и во многих других отраслях промышленности. Обычно целью решения этих задач является нахождение коорди­наты фронта фазового превращения в заданный момент времени, определение скорости перемещения границы раздела фаз и пол­ной длительности либо нагрева и плавления твердого тела с из­вестными размерами, либо охлаждения и затвердевания некото­рого объема расплава.

Как следует из условия Стефана (2.12), скорость и направле­ние фазового превращения однозначно определяется величиной плотности результирующего теплового потока на межфазной гра­нице, т.е. разностью плотностей подводимого к границе и отво­димого от нее тепловых потоков. Значения этих потоков обус­ловлены полями температур в твердой и жидкой фазах. Поэтому ответы на поставленные вопросы следует в общем случае искать путем постановки задач теплопроводности для твердой и жидкой фаз, сопрягаемых на межфазной границе посредством условия Стефана и равенства температур обеих фаз.

При этом должны быть учтены все рассмотренные выше особенности протекания тепловых процессов при изменении агрегат­ного состояния, учитывающие степень тепловой массивности тел, поведение образующейся при плавлении жидкой фазы, геометри­ческие характеристики изучаемой системы и т.д. Все эти сведения позволяют корректно сформулировать начальные и граничные ус­ловия для решения уравнений теплопроводности, которое в общем случае может быть получено с помощью численных методов.

Далее будут рассмотрены некоторые задачи плавле­ния и затвердевания, для которых существуют либо строгие, либо приближенные аналитические решения. Целью получения этих ре­шений является не столько вывод расчетных формул для каких-либо конкретных случаев, сколько проведение количественного ана­лиза тех закономерностей

тепловых процессов при плавлении и затвердевании, которые качественно описаны в настоящей главе. Поэтому при постановке и решении рассматриваемых ниже задач принимаются следующие ограничения и упрощающие допущения:

• тепловые потоки считаются одномерными, а фронты изуча­емых фазовых превращений плоскими;

• все теплофизические характеристики вещества не зависят от температуры;

• рассматриваемые тела однородны и состоят из чистого кристаллического вещества с постоянной температурой фазового превращения;

• в случае передачи тепла к фронту фазового превращения от внешнего источника коэффициент теплоотдачи и температура ис­точника считаются постоянными.

Затвердевание расплава на теплоотводящей поверхности. Рассмотрим процесс затвердевания расплава, вступающего в контакт с плоской теплоотводящей поверхностью, имеющей по­стоянную температуру Т_о < Т_пр. В начальный момент времени ξ(0) = 0, q' → ∞ и ν → ∞. По мере увеличения толщины затвердевшего слоя плотность теплового потока q', отводимого внутрь твердой фазы, умень­шается, и, соответственно, падает скорость затвердевания v (ν → 0 при t → ∞). Требу­ется определить температурное поле в за­твердевшем слое Т(х, t) (рис. 25.1, начало координат х = 0 соответствует теплоотводящей поверхности) и изменение во времени толщины затвердевшего слоя ξ(t).

Предположим сначала, что перегрев расплава над температурой его затвердева­ния отсутствует, т.е. температура расплава постоянна по всему его объему и равна Т_пр. В этом случае плотность внешнего теплового потока q = 0, и из условия Сте­фана (2.12) следует, что скорость затвердевания расплава опреде­ляется только плотностью теплового потока q', однозначно зави­сящей от распределения температуры в затвердевшем слое.

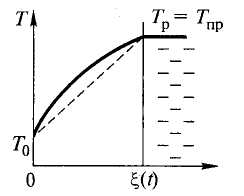
Рис. 2.6. Распределение температуры по толщине слоя затвердевшего расплава в момент времени t

Для получения точного (аналитического) решения задачи не­обходимо произвести ее строгую математическую формулировку, включающую в себя:

— одномерное уравнение теплопроводности в области с движущейся границей

0 < x < ξ(t); (2.13)

— начальное условие

ξ (0) = 0; (2.14)

— граничное условие на теплоотводяшей поверхности

(2.15)

— граничные условия на движущейся межфазной поверхности

(2.16)

(2.17)

(последнее соотношение следует из условия Стефана (2.12) при q = 0). Система уравнений (2.13)—(2.15) определяет две неизвест­ные функции: Т(х, t) и ξ(t).

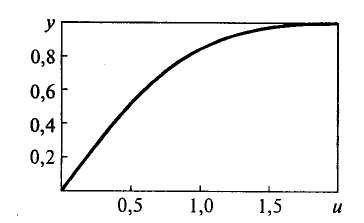
Рис. 2.7. График функции ошибок у = erf(u)

Для нахождения обобщенного решения перейдем от темпера­туры Т_к безразмерной температуре = (Т — Т₀)/(Т_пр — T₀), а от времени t к вспомогательной переменной τ = at. Получим:

— уравнение теплопроводности

0 < x < ξ(t); (2.18)

— начальное условие

ξ (0) = 0; (2.19)

• граничное условие на охлаждаемой поверхности

|_х=0 = 0; (2.20)

• граничные условия на движущейся межфазной поверхности

(2.21)

(2.22)

здесь

— критерий Коссовича, характеризующий влияние безразмер­ной плотности теплового потока, отводимого внутрь твердой фазы, на скорость перемещения границы раздела фаз (иногда величину 1/К₀ называют критерием Стефана).

Для решения задачи теплопроводности (2.18) —(2.22) при­меним метод выпрямления фронта, заключающийся в переходе от расчетной области с движущейся границей 0 ≤ x ≤ ξ(t) к фик­сированной расчетной области 0 ≤ η ≤ 1, где относительная коор­дината

При этом переходе

и задача теплопроводности (2.18) — (2.22) преобразуется следующим образом:

0 < η < 1 (2.23)

ξ(0) = 0; (2.24)

(2.25)

(2.26)

(2.27)

Будем искать решение задачи (2.23) — (2.27), удовлетворяю­щее «закону квадратного корня»

или

(25.28)

где коэффициент , подлежащий определению, называется кон­стантой скорости затвердевания. При этом

(2.29)

и граничное условие (25.15) принимает вид

(2.30)

Из соотношений (2.23), (2.24) и (2.30) следует, что в обла­сти 0 ≤ η ≤ 1 температурное поле не зависит от времени, поэтому уравнение теплопроводности (2.23) переходит в обык­новенное дифференциальное уравнение

, 0 < η < 1 (2.31)

После замены переменной вместо (2.31) получим

откуда

и

(2.32)

где erf (u) = - функция ошибок Гаусса (график этой функции представлен на рис. 2.7).

Решение (2.32) удовлетворяет граничному условию (2.25). Для нахождения постоянной интегрирования С используем гра­ничное условие (2.26):

откуда

и окончательно имеем

(2.33)

Из последнего соотношения следует, что форма безразмерного распределения температуры по толщине затвердевшего слоя зависит только от константы у, т.е., в конечном итоге, от критерия Коссовича.

Для определения константы скорости затвердевания у исполь­зуем граничное условие (2.26), после преобразования которого получим нелинейное уравнение

(2.34)

Результаты решения этого уравнения методом простой итера­ции приведены в таблице 2.2. В этой же таблице указаны зна­чения безразмерных градиентов температуры на теплоотводящей поверхности (0) и на межфазной поверхности '(1), найденные по формулам

(2.35)

(2.36)

После определения константы скорости затвердевания у изме­нение во времени толщины затвердевшего слоя ξ(t) определяется по формуле (2.27).

Таблица 2.2. Значения параметров, используемых для описания процесса зат­вердевания расплава на охлаждаемой поверхности

К0 γ

0,1 1,2570 1,5341 0,3160 0,2 1,0597 1,3807 0,4492 0,3 0,9437 1,3018 0,5343 0,4 0,8624 1,2518 0,5950 0,5 0,8006 1,2167 0,6410 1,0 0,6201 1,1295 0,7690 10 0,2200 1,0162 0,9682 100 0,0706 1,0017 0,9968

Данные, представленные в табл. 2.2, свидетельствуют о том, что при увеличении критерия Коссовича безразмерные градиен­ты и стре­мятся к единице, т. е. распределение температуры по толщине затвердевшего слоя приближается к линейному, показанному на рис. 2.6 пунктирной прямой. Поскольку линей­ное распределение температуры в плоском слое соответствует стационарному режиму переноса тепла, режим затвердевания расплава при К₀ → ∞ может быть назван квазистационарным.

Определим константу скорости затвердевания в квазистацио­нарном приближении. Если распределение температуры по сече­нию затвердевшего слоя в каждый момент времени является ли­нейным (пунктирная прямая на рис. 2.6), плотность теплового потока, отводимого от межфазной поверхности, равна

Подставив это выражение в соотношение (2.12), получим

, или

Решение полученного обыкновенного дифференциального уравнения (при начальном условии ξ(0) = 0) имеет общий вид (25.16), где константа скорости затвердевания

(2.35)

В общем случае процесс нестационарного теплообмена назы­вается квазистационарным, если изменение условий формирова­ния температурного поля происходит настолько медленно, что в каждый момент времени тепловой режим можно приближенно считать стационарным. Поскольку в рассматриваемом случае причиной нестационарности

температурного поля является дви­жение межфазной границы, квазистационарное приближение справедливо при достаточно малых скоростях затвердевания рас­плава, т. е. малых значениях у. Таким образом, формула (2.35) оказывается применимой при достаточно больших значениях кри­терия Коссовича (К₀ → ∞).