Тема 1.2. Основные операции над множествами.
Самостоятельная работа №2.
Тема: Изучить аксиомы множеств, алгоритм доказательства тождества множеств, доказать законы двойственности, законы поглощения.
Время выполнения задания – 2ч.
Цель работы: Закрепление знаний по свойствам и аксиомам множеств, а также тождествам и законам.
Теоретический материал.
Для любых
подмножеств
,
,
С и универсального множества
рассмотрим следующие тождества:
1.
– коммутативность объединения;
2.
– ассоциативность объединения;
3.
– дистрибутивность объединения
относительно пересечения;
4.
Ø
;
5.
;
6.
;
7.
;
8.
– закон де Моргана;
9.
– закон поглощения.
1*.
– коммутативность пересечения;
2*.
– ассоциативность пересечения;
3*.
– дистрибутивность пересечения
относительно объединения;
4*.
;
5*.
Ø;
6*.
;
7*.
Ø
Ø;
8*.
– закон де Моргана;
9*.
– закон поглощения.
Введём новое
понятие: упорядоченная пара
– это совокупность, состоящая из двух
элементов
и
,
расположенных в определённом порядке.
Прямым или декартовым
произведением множеств
и
называется совокупность всех упорядоченных
пар
таких, что
и
.
Обозначается:
.
Пример:
Пусть
и
,
тогда
;
.
Таким образом,
.
Вопросы для самоконтроля:
1. Запишите коммутативность, ассоциативность и ассоциативность объединения.
2. Что такое закон де Моргана?
3. Запишите коммутативность, ассоциативность и ассоциативность пересечения.
4. Что такое закон поглощения?
Рекомендуемая литература:
Основные источники:
1. Дискретная математика : учебник для студ. учреждений сред. проф. образования / М.С.Спирина, П.А.Спирин. —. 7-е изд., стер. — М. : Издательский центр «Академия», 2012. —. 368 с.
2. М.С.Спирина, П.А.Спирин. Дискретная математика. Изд-во Академия/Academia", 2010 г.
Дополнительные источники:
1. Гончарова Г.А., Мочалин А.А. Элементы дискретной математики. М. Форум - инфри - м 2003 г. 2. Горбатов В.А. Основы дискретной математики. М. Наука 1986 г. 3. Карпов В.Г., Мощенский В.А. Математическая наука и Дискретная математика. Минск. Винца школа 1977 г. 4. Кузнецов О.П., Адельсон - Вильский Г.М. Дискретная математика для инженера. Энергоатомиздат, 1998 г.
Интернет ресурсы:
1. М.М. Арсланов, И.Ш. Калимуллин. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ.http://www.ksu.ru/f5/k2/bin_files/logika!13.pdf
2. Гиндикин С.Г. Алгебра логики в задачах. Электронная библиотека Московского государственного университета. http://lib.mexmat.ru/books/1383
Самостоятельная работа №3.
Тема: Решение задач с использованием аппарата теории множеств.
Время выполнения задания – 2ч.
Цель работы: Закрепление знаний и умений по операциям над множествами.
Теоретический материал.
С помощью некоторых операций из данных множеств можно получить новые множества. Эти операции в некотором смысле аналогичны алгебраическим операциям над числами. Рассмотрим их:
1. Объединением множеств и называется такое множество, элементы которого являются элементами множества или множества .
Обозначается:
.
или
.
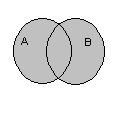
2. Пересечением множеств и называется такое множество, элементы которого являются элементами множества и множества .
Обозначается:
.
и
.
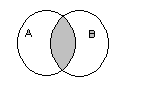
3. Разностью множеств и называется такое множество, элементами которого являются элементы множества , не принадлежащие множеству .
Обозначается:
.
и
.
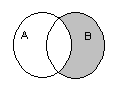
4. Симметричной разностью множеств и называется множество:
или
.
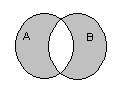
5. Абсолютным
дополнением множества
называется множество
(не
)
всех тех элементов
,
которые не принадлежат множеству
.
.
Для наглядного представления отношений между множествами используют круги Эйлера.
Вопросы для самоконтроля:
1. Дайте определение объединение множеств.
2. Что такое пересечение множеств?
3. Дайте определение разности множеств.
4. Что такое симметричная разность множеств?
5. Что такое абсолютное дополнение множество?
Рекомендуемая литература:
Основные источники:
1. Дискретная математика : учебник для студ. учреждений сред. проф. образования / М.С.Спирина, П.А.Спирин. —. 7-е изд., стер. — М. : Издательский центр «Академия», 2012. —. 368 с.
2. М.С.Спирина, П.А.Спирин. Дискретная математика. Изд-во Академия/Academia", 2010 г.
Дополнительные источники:
1. Гончарова Г.А., Мочалин А.А. Элементы дискретной математики. М. Форум - инфри - м 2003 г. 2. Горбатов В.А. Основы дискретной математики. М. Наука 1986 г. 3. Кузнецов О.П., Адельсон - Вильский Г.М. Дискретная математика для инженера. Энергоатомиздат, 1998 г. 4. Нефедов В.Н., Осипова В.А. Курс дискретной математики. М. Издательство МАИ 1992 г.
Интернет ресурсы:
1. М.М. Арсланов, И.Ш. Калимуллин. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ.http://www.ksu.ru/f5/k2/bin_files/logika!13.pdf
2. Гиндикин С.Г. Алгебра логики в задачах. Электронная библиотека Московского государственного университета. http://lib.mexmat.ru/books/1383