Раздел 2. Теория графов.(24ч.)
Тема 2.1. Основные понятия и определения графа и его элементов.
Самостоятельная работа №13. Изучить правило игры, придуманные Гамильтоном в XIX веке, задачу о коммивояжере - задачу математического программирования.
Тема 2.2. Операции над графами.
Самостоятельная работа №14. Операции над графами. Кольцевая сумма.
Тема 2.3. Способы задания графа.
Самостоятельная работа №15.Граф Эйлера.
Тема 2.4. Сети. Сетевые модели представления информации.
Самостоятельная работа №16. Представление иерархических структур с помощью графов.
Раздел 3. Математическая логика.(36ч.)
Тема 3.1. Понятие как форма мышления.
Самостоятельная работа №17. Определение объема и содержания данного понятия.
Тема 3.2. Суждение как форма мышления.
Самостоятельная работа №18. Определение понятий. Операции над понятиями. Деление понятий. Классификация.
Тема 3.3. Булевы функции.
Самостоятельная работа №19. Доказательство законов алгебры логики.
Самостоятельная работа №20. Тождественные преобразования формул с использованием законов алгебры логики.
Самостоятельная работа №21.Логика вопросов и ответов.
Тема 3.4. Минимизация булевых функций.
Самостоятельная работа №22. Представление булевых функций в виде формул заданного типа.
Самостоятельная работа №23. Карты Карно для булевых функций трех (четырех) переменных. Связь булевых функций с суммой по модулю два.
Тема 3.5. Полином Жегалкина.
Самостоятельная работа №24. Проверить, являются ли функционально замкнутыми классы: а) S - класс самодвойственных функций; б) L - класс линейных функций; в) М - класс монотонных функций. Изучить примеры доказательства полноты системы, например {+,V,1} составив таблицы Поста.
Раздел 4. Формальные системы и умозаключения. Логика предикатов.(20ч.)
Тема 4.1. Формальные системы.
Самостоятельная работа №25. Автоматизация исчисления высказываний с использованием установленных правил.
Самостоятельная работа №26. Отличительные особенности геометрии Лобачевского и геометрии Евклида.
Тема 4.2. Логика предикатов.
Самостоятельная работа №27. Умозаключения как форма мышления. Дедуктивные умозаключения и их виды.
Самостоятельная работа №28. Простые категорические силлогизмы. Энтимемы.
Тема 4.3. Методы научного познания.
Самостоятельная работа №29. Методы установления причинных связей. Метод Милли.
Раздел 1. Теория множеств.(36ч.)
Тема 1.1. Общие понятия теории множеств Язык теории множеств.
Самостоятельная работа №1.
Тема: Изучить свойства счетных множеств.
Время выполнения задания – 2ч.
Цель работы: Закрепление знаний по свойствам счетных множеств.
Теоретический материал.
Определение: Множество представляет собой совокупность некоторых предметов (объектов), объединённых по какому-либо признаку.
Определение: Предметы (объекты), из которых состоит множество, называются элементами этого множества.
Примеры множества: множество натуральных чисел, множество книг на полке, множество студентов, учащихся в вашей группе.
Элементы множества
обозначаются малыми латинскими и
греческими буквами:
или
,
а множества обозначаются заглавными
буквами латинского алфавита:
.
Например, множество
чисел, состоящих из элементов
можно записать в виде:
.
Используют и другую
форму записи множества. Например,
множество положительных целых чисел
меньше 9 можно записать в виде:
=
или
=
.
Символом
обозначается отношение принадлежности.
Запись
означает, что элемент
принадлежит множеству
.
Запись
означает, что элемент
не принадлежит множеству
.
Множества и считаются равными, если они состоят из одних и тех же элементов.
Примеры:
1. Пусть
,
,
тогда
.
2.
.
Если любой элемент
множества
является и элементом множества
,
то множество
называют подмножеством множества
и говорят, что
содержится в
,
т. е.
,
где
– знак включения.
Пример:
Пусть дано множество натуральных чисел
и множество целых чисел
.
Видим, что
,
значит множество натуральных чисел
является подмножеством множества целых
чисел.
Заметим, что:
а).
;
б). Если
и
,
то
;
в). Если
и
,
.
Определение: Множество, которое не содержит ни одного элемента, называется пустым множеством и обозначается Ø.
Пример: Множество точек пересечения параллельных прямых является пустым множеством.
Пустое множество
и само множество
называются несобственными подмножествами
множества
,
т. е. Ø
,
.
Рассмотрим множество
.
Выпишем все его подмножества:
Ø,
.
Решите примеры.
Запищите множество всех целых чисел от -5 до 5.
Запишите множество всех четных натуральных чисел от 2 до 20.
Пусть
,
,
,
.
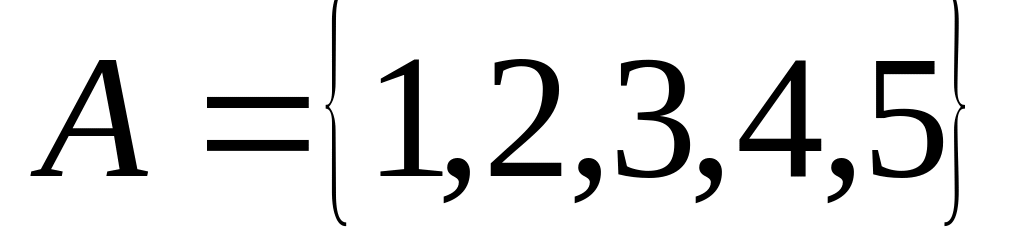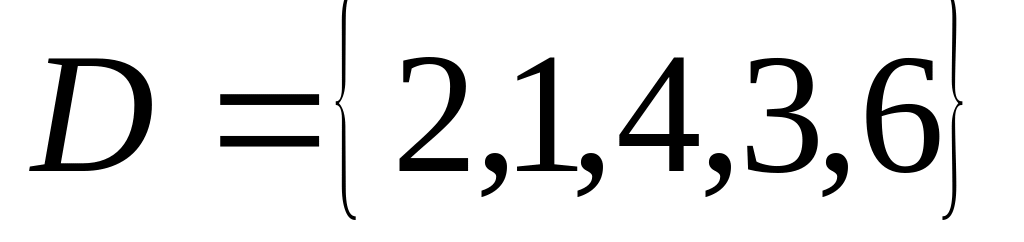Определите, какие множество равны.Пусть
.
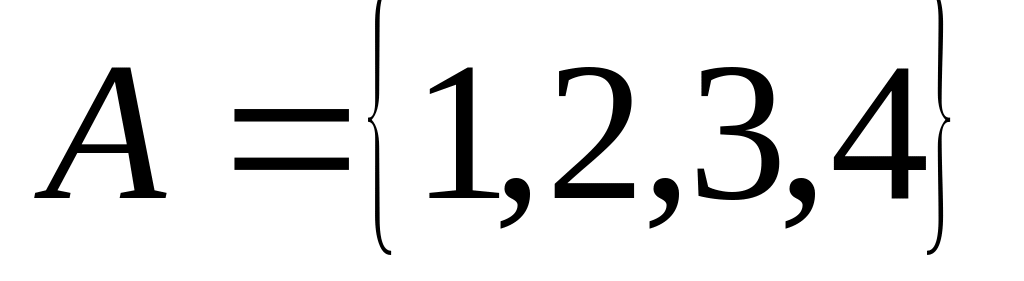Выпишите все его подмножества.
Вопросы для самоконтроля:
1. Дайте определение множество.
2. Что такое элемент множество?
3. Что такое равные множества?
4. Что такое пустое множество?
Рекомендуемая литература:
Основные источники:
1. Дискретная математика : учебник для студ. учреждений сред. проф. образования / М.С.Спирина, П.А.Спирин. —. 7-е изд., стер. — М. : Издательский центр «Академия», 2012. —. 368 с.
2. М.С.Спирина, П.А.Спирин. Дискретная математика. Изд-во Академия/Academia", 2010 г.
Дополнительные источники:
1. Вентцель Е.С. «Исследование операций, задачи, принципы, методология» М. Наука 1988 г. 2. Гончарова Г.А., Мочалин А.А. Элементы дискретной математики. М. Форум - инфри - м 2003 г. 3. Горбатов В.А. Основы дискретной математики. М. Наука 1986 г.
Интернет ресурсы:
1. М.М. Арсланов, И.Ш. Калимуллин. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ.http://www.ksu.ru/f5/k2/bin_files/logika!13.pdf
2. Гиндикин С.Г. Алгебра логики в задачах. Электронная библиотека Московского государственного университета. http://lib.mexmat.ru/books/1383