Основные источники:

1. Дискретная математика : учебник для студ. учреждений сред. проф. образования / М.С.Спирина, П.А.Спирин. —. 7-е изд., стер. — М. : Издательский центр «Академия», 2012. —. 368 с.

Дополнительные источники:

1. Вентцель Е.С. «Исследование операций, задачи, принципы, методология» М. Наука 1988 г. 2. Гончарова Г.А., Мочалин А.А. Элементы дискретной математики. М. Форум - инфри - м 2003 г. 3. Горбатов В.А. Основы дискретной математики. М. Наука 1986 г. 4. Карпов В.Г., Мощенский В.А. Математическая наука и Дискретная математика. Минск. Винца школа 1977 г. 5. Кузнецов О.П., Адельсон - Вильский Г.М. Дискретная математика для инженера. Энергоатомиздат, 1998 г. 6. Нефедов В.Н., Осипова В.А. Курс дискретной математики. М. Издательство МАИ 1992 г.

Интернет ресурсы:

1. М.М. Арсланов, И.Ш. Калимуллин. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ.http://www.ksu.ru/f5/k2/bin_files/logika!13.pdf

2. Гиндикин С.Г. Алгебра логики в задачах. Электронная библиотека Московского государственного университета. http://lib.mexmat.ru/books/1383

Раздел 4. Формальные системы и умозаключения. Логика предикатов.(20ч.)

Тема 4.1. Формальные системы. Самостоятельная работа №25.

Тема: Автоматизация исчисления высказываний с использованием установленных правил.

Время выполнения задания – 2ч.

Цель работы: Закрепление знаний по автоматизации исчисления высказываний с использованием установленных правил.

Теоретический материал.

В обычной жизни человек принимает решения в зависимости от конкретной ситуации. Предположим, что нам известны некоторые факты (или ранее уже доказанные утверждения) F₁, F₂, ..., F_n, и нас интересует, следует ли некоторое утверждение G из утверждений F₁, F₂, ..., F_n. Утверждение, что G логически следует из утверждений F₁, F₂, ..., F_n называют теоремой. Доказательство теоремы — рассуждения, позволяющие установить, что теорема верна.

Одной из задач математической логики является формализация понятия доказательства.

Для описания утверждений можно использовать формулы исчисления высказываний. Каждое высказывание либо истинно, либо ложно. Можно строить составные высказывания, используя логические связки, отрицание(~), конъюнкцию(&), дизъюнкцию(v), импликацию(=>) и эквивалентность(<=>). Логические константы "истина" и "ложь" будем обозначать буквами И и Л соответственно. Логические переменные (в математической логике их называют пропозициональные переменные) будем обозначать большими буквами латинского алфавита.

Унарная связка ~ меняет значение высказывания на противоположное. В табл.1 представлены результаты логических связок таблицы истинности.

Таблица 1. Таблица истинности бинарных связок

А	B	А&В	AvB	А=>В	А<=>В
и	и	и	и	и	и
и	л	л	и	л	л
л	и	л	и	и	л
л	л	л	л	и	и

В исчислении высказываний логические константы и логические переменные называются атомами и считаются простейшими логическими формулами. Кроме атомов логической формулой считается отрицание логической формулы, а также (F1 + F2), где F1, F2— логические формулы, а знак Ф обозначает одну из бинарных логических связок. Других формул в исчислении высказываний нет.

Вычисление значения постоянной логической формулы.

Создадим сценарий, который облегчает ввод постоянных пропозициональных формул. При нажатии кнопки, соответствующей логическим константам или логическим операциям, определенная операция появляется в поле ввода так, как показано на рис. 1. После построения формулы и нажатия кнопки вычислить определяется значение формулы.

Напомним, что при построении логических формул в языке JavaScript разрешено использовать три логические операции: отрицание (!), логическое И (&&) и логическое ИЛИ (||). При нажатии кнопки соответствующая операция появляется в текстовом поле, причем знак операции должен быть тем, который принят в языке JavaScript.

Подобная формула может быть вычислена, если подать ее в качестве параметра методу eval. Если же формула содержит знаки импликации (=>) и логической эквивалентности (<=>), то требуется провести анализ формулы и вычислить ее значение с помощью определяемых программистом функций. HTML-код документа, содержащего сценарий решения задачи, представлен в листинге на рис. 1.

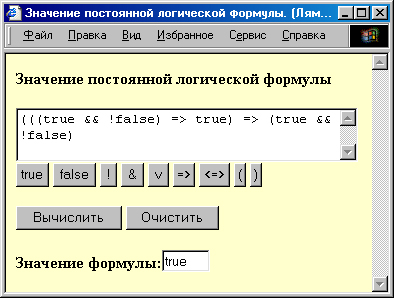
Рис. 1. Построитель постоянных логических форм

Если задать значения всем входящим в формулу переменным, то можно вычислить результат всей формулы. В этом случае говорят, что задана интерпретация. В исчислении высказываний каждой формуле соответствует конечное число интерпретаций.

Вычисление значения формулы в заданной интерпретации.

Необходимо написать сценарий вычисления значения логической формулы в заданной интерпретации. Пусть при построении формулы используются только три переменные а, b, с, значения которых указывает пользователь. Для ввода логической формулы применяется построитель формул так, как показано на рис. 2.

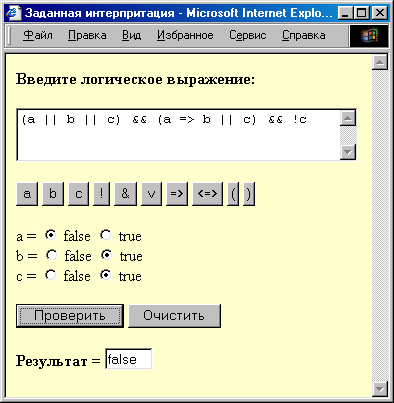
Рис. 2. Значение формулы

Соотношение формул.

В общем случае при анализе формулы следует учесть количество различных переменных, входящих в формулу. Так как каждая переменная может принимать только два значения, то число различных интерпретаций конечно.

Формулы бывают тождественно истинными (или общезначимыми) — это формулы истинные в любой интерпретации. Тождественно ложными (или противоречивыми) называются формулы, ложные в любой интерпретации.

Наконец, выполнимыми называются формулы, допускающие указание интерпретации, в которой эта формула истинна. Если две формулы имеют одинаковые значения при любых возможных интерпретациях, то говорят, что они равнозначны или эквивалентны. Равнозначность формул обозначают знаком «о». Обозначим знаком «о» любую общезначимую формулу и знаком «П» любую противоречивую формулу.

Наиболее распространенные равнозначные формулы приведены в табл. 2.

Таблица 2. Равнозначные формулы

Формула	Формула
А <-> B <-> (~ A v B) & (~ В vА)  (А => В) <-> ~ A v B  A v (S v С) <-> (A v B) v С A v B <-> B v A A v (B & C) <-> (A v B) & (A v C) ~ (~A) <-> A A v ~ A <->A  A v <->A ~ (A v B) <-> ~ A & ~ B	А & (В & С) <-> (А & В) & С А & В <-> В & А А & (В v С) <-> (А & B) v (А & С) A & ~ A <-> А & <-> A & <-> A ~ (A & В) <-> ~ A v ~ B

Нетрудно доказать, что любую формулу исчисления высказываний можно преобразовать к равнозначной формуле, которая содержит только три логические связки: отрицание, конъюнкцию и дизъюнкцию. Действительно доказав равнозначность формул А => В и ~А v В, а также формул A<=>B и (A & B) v (~А & ~B), получим то, что требуется. Некоторые часто используемые правила получили специальные названия, например:

•  закон двойного отрицания: ~ ~ А <-> А; 

• закон контрапозиции: А => В <-> ~ В => ~ А; 

• законы де Моргана: ~ (A v B) <-> ~ А & ~ В и ~ (А & B) <-> ~ A v ~ B.

Пусть заданы две формулы (A => B) => С и A => (В => С). Требуется определить, эквивалентны ли они. Для того чтобы решить задачу, мы переберем все интерпретации и в каждой из интерпретаций вычислим значение формулы. Результаты приведены в табл. 3.

Таблица 3. Таблица истинности для формул (А => В) => С и А =* (В =>С)

№	А	B	C	(А=>В)=>С	А=> (В => С)
1	и	и	и	и	и
2	и	и	л	л	л
3	и	л	и	и	и
4	и	л	л	и	и
5	л	и	и	и	и
6	л	и	л	л	и
7	л	л	и	и	и
8	л	л	л	л	и

После вычислений видно, что значения формул не совпадают в некоторых интерпретациях, поэтому заданные формулы неравнозначны.

Построение таблицы истинности.

Напишем сценарий, который для логической формулы строит таблицу истинности. В формуле разрешено использовать операции отрицания, дизъюнкции и конъюнкции; переменные представляются буквами латинского алфавита. Вид документа представлен на рис. 3.

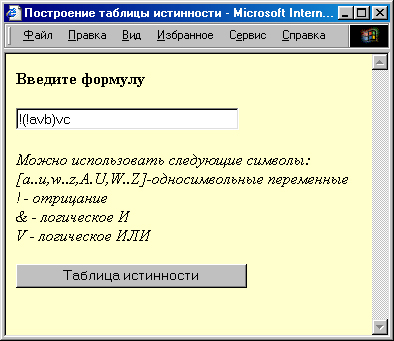
Рис. 3. Формирование таблицы истинности для заданной формулы

Если после ввода формулы нажать кнопку таблица истинности, то будет выведена таблица, в которой указаны все возможные интерпретации и значение формулы в каждой интерпретации. Для формулы, введенной в строку на рис. 3, будет сформирован следующий документ, содержащий таблицу истинности (рис. 4).

Рис. 4. Таблица истинности для заданной формулы

Вопросы для самоконтроля:

1. Запишите закон двойного отрицания.

2. Запишите закон контрапозиции.

3. Что такое тождественно-истинные формула?

4. Что такое тождественно-ложные формула?

Рекомендуемая литература: