Основные источники:
1. Дискретная математика : учебник для студ. учреждений сред. проф. образования / М.С.Спирина, П.А.Спирин. —. 7-е изд., стер. — М. : Издательский центр «Академия», 2012. —. 368 с.
2. М.С.Спирина, П.А.Спирин. Дискретная математика. Изд-во Академия/Academia", 2010 г.
Дополнительные источники:
1. Вентцель Е.С. «Исследование операций, задачи, принципы, методология» М. Наука 1988 г. 2. Гончарова Г.А., Мочалин А.А. Элементы дискретной математики. М. Форум - инфри - м 2003 г. 3. Горбатов В.А. Основы дискретной математики. М. Наука 1986 г. 4. Карпов В.Г., Мощенский В.А. Математическая наука и Дискретная математика. Минск. Винца школа 1977 г. 5. Кузнецов О.П., Адельсон - Вильский Г.М. Дискретная математика для инженера. Энергоатомиздат, 1998 г. 6. Нефедов В.Н., Осипова В.А. Курс дискретной математики. М. Издательство МАИ 1992 г.
Интернет ресурсы:
1. М.М. Арсланов, И.Ш. Калимуллин. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ.http://www.ksu.ru/f5/k2/bin_files/logika!13.pdf
2. Гиндикин С.Г. Алгебра логики в задачах. Электронная библиотека Московского государственного университета. http://lib.mexmat.ru/books/1383
Самостоятельная работа №21.
Тема: Логика вопросов и ответов.
Время выполнения задания – 2ч.
Цель работы: Закрепление знаний по логике вопросов и ответов.
Напишите конспект по теме и ответе на контрольные вопросы.
Вопросы для самоконтроля:
1. С точки зрения логики, что такое «вопрос»?
2. С точки зрения логики, что такое «ответ»?
3. Что такое «открытие» и «закрытие» вопросы?
4. Перечислите типы вопросов.
Рекомендуемая литература:
Основные источники:
1. Дискретная математика : учебник для студ. учреждений сред. проф. образования / М.С.Спирина, П.А.Спирин. —. 7-е изд., стер. — М. : Издательский центр «Академия», 2012. —. 368 с.
2. М.С.Спирина, П.А.Спирин. Дискретная математика. Изд-во Академия/Academia", 2010 г.
Дополнительные источники:
1. Вентцель Е.С. «Исследование операций, задачи, принципы, методология» М. Наука 1988 г. 2. Гончарова Г.А., Мочалин А.А. Элементы дискретной математики. М. Форум - инфри - м 2003 г. 3. Нефедов В.Н., Осипова В.А. Курс дискретной математики. М. Издательство МАИ 1992 г. 4. Нефедов Ф.А. Дискретная математика для программистов. СПб – Питер. 2001 г. 5. Яблонский С.В. Введение в дискретную математику. М. Наука, 1986 г., 384с.
Интернет ресурсы:
1. М.М. Арсланов, И.Ш. Калимуллин. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ.http://www.ksu.ru/f5/k2/bin_files/logika!13.pdf
2. Гиндикин С.Г. Алгебра логики в задачах. Электронная библиотека Московского государственного университета. http://lib.mexmat.ru/books/1383
Тема 3.4. Минимизация булевых функций. Самостоятельная работа №22.
Тема: Представление булевых функций в виде формул заданного типа.
Время выполнения задания – 2ч.
Цель работы: Закрепление знаний по представлению булевых функций в виде формул заданного типа.
Теоретический материал.
Определение: Булевой функцией f(x1, x2, …, xn) называется n-местная функция, аргументы которой принимают значения во множестве {0, 1} и сама функция принимает значения в этом же множестве.
Всякую булеву функцию от n переменных можно задать таблицей из 2n строк, в которой в каждой строке записывают одну из оценок списка переменных, принимающих значение 0 или 1.
Пример 1. Для n=3 булеву функцию можно задать таблицей 1.
Таблица 1
№ |
x1 |
x2 |
x3 |
f(x1, x2, x3) |
0 |
0 |
0 |
0 |
f(0, 0, 0) |
1 |
0 |
0 |
1 |
f(0, 0, 1) |
2 |
0 |
1 |
0 |
f(0, 1, 0) |
3 |
0 |
1 |
1 |
f(0, 1, 1) |
4 |
1 |
0 |
0 |
f(1, 0, 0) |
5 |
1 |
0 |
1 |
f(1, 0, 1) |
6 |
1 |
1 |
0 |
f(1, 1, 0) |
7 |
1 |
1 |
1 |
f(1, 1, 1) |
Используется также задание булевой функции в виде двоичного слова, длина которого зависит от числа переменных.
Пример 2.
Пусть
задана булева функция от трех переменных
(табл. 2). Тогда число наборов 
.
Таблица 2
№ набора |
х1 |
х2 |
х3 |
f |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
2 |
0 |
1 |
0 |
1 |
3 |
0 |
1 |
1 |
0 |
4 |
1 |
0 |
0 |
1 |
5 |
1 |
0 |
1 |
1 |
6 |
1 |
1 |
0 |
0 |
7 |
1 |
1 |
1 |
1 |
Номера наборов всегда нумеруются, начиная с нуля, в таблице приведено стандартное расположение всех наборов функции трех переменных (обратите внимание, что каждый набор представляет собой двоичный код числа, равный номеру соответствующего набора). Первые четыре столбца одинаковы для всех булевых функций от трех переменных. Столбец значений функции задается или вычисляется.
Эту же функцию можно записать f(х1, х2, х3)=00101101.
Существует
ровно 
различных
булевых функций от n переменных.
Константы 0 и 1 считают нуль-местными
булевыми функциями.
Утверждение. Каждой формуле логики высказываний соответствует некоторая булева функция.
Теорема. Пусть f(x1, x2, …, xk) k-местная булева функция. Если f не равна тождественно нулю, то существует такая формула F, зависящая от списка переменных x1, x2, …, xn и находящаяся в СДНФ относительно этого списка, что F выражает собой функцию f. Формула F определена однозначно с точностью до перестановки дизъюнктивных членов.
Вопросы для самоконтроля:
1. Дайте определения булевой функции.
2. В каком виде можно задать булевую функцию?
3. Как можно представлять булевую функцию?
4. Сформулируйте теорему о СДНФ?
Рекомендуемая литература:
Основные источники:
1. Дискретная математика : учебник для студ. учреждений сред. проф. образования / М.С.Спирина, П.А.Спирин. —. 7-е изд., стер. — М. : Издательский центр «Академия», 2012. —. 368 с.
Дополнительные источники:
1. Кузнецов О.П., Адельсон - Вильский Г.М. Дискретная математика для инженера. Энергоатомиздат, 1998 г. 2. Нефедов В.Н., Осипова В.А. Курс дискретной математики. М. Издательство МАИ 1992 г. 3. Нефедов Ф.А. Дискретная математика для программистов. СПб – Питер. 2001 г.
Интернет ресурсы:
1. М.М. Арсланов, И.Ш. Калимуллин. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ.http://www.ksu.ru/f5/k2/bin_files/logika!13.pdf
2. Гиндикин С.Г. Алгебра логики в задачах. Электронная библиотека Московского государственного университета. http://lib.mexmat.ru/books/1383
Самостоятельная работа №23.
Тема: Карты Карно для булевых функций трех (четырех) переменных. Связь булевых функций с суммой по модулю два.
Время выполнения задания – 2ч.
Цель работы: Закрепление знаний по карты Карно для булевых функций трех (четырех) переменных, а также Связь булевых функций с суммой по модулю два.
Напишите реферат по теме и ответе на контрольные вопросы.
Теоретический материал.
Минимизация Булевых функций. Карты Карно.
Под минимизацией Булевых функций понимают упрощение исходного алгебраического выражения до вида, требующего для практической реализации минимального количества полупроводниковых структур.
Исходным для минимизации является алгебраическая форма представления Булевых функций. Процедура минимизации опирается на применение основных теорем Булевой алгебры. Критерием успешной минимизации является соотношение между исходным количеством полупроводниковых структур, и их количеством в окончательном варианте.
Количество полупроводниковых структур определяется по следующим правилам:
Одни выход логического элемента И или ИЛИ эквивалентен одному полупроводниковому диоду. Анализ нелинейных цепей Общие понятия об элементах нелинейных цепей Цепи, которые изучались ранее, относятся к классу линейных цепей. Параметры элементов этих цепей. Параметры элементов этих цепей - сопротивлений, индуктивностей, емкостей - не зависит от значений приложенных к ним напряжений или протекающих через них токов.
Операция НЕ эквивалентна одному полупроводниковому транзистору.
Например:
здесь:
4 – диода, 1 – транзистор.
Рассмотрим технологию минимизации на примерах (из предыдущего параграфа), исходная алгебраическая форма:
Пример
1: 
=
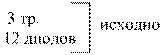
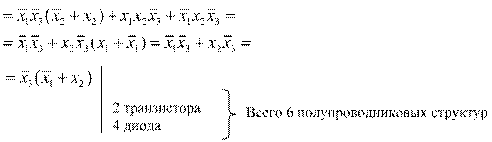
Минимизация завершена.
Пример 2:
В тех случаях, когда количество переменных больше трех, удобнее пользоваться не последовательными алгебраическими вычислениями, а специальными картами, которые позволяют автоматизировать процесс минимизации. Это карты Карно.
Основополагающим для составления карт Карно является два термина.
Ранг слагаемого – это количество двоичных переменных, образующих элементарное произведение.
Соседние
элементы – такие элементарные
произведения, которые отличаются друг
от друга только на одну инверсию.
Например: 
.
Рассмотрим построение карт Карно на примере 4-х переменных. Вид шаблона карт Карно следующий:
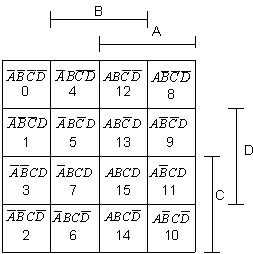
A, B, C, D - двоичные переменные
Боковые и верхние ризки указывают на то, что переменные в этих полях при построении этих элементарных произведений берутся без инверсии, в противном случае – с инверсией. Каждая ячейка – элементарное произведение всех четырех переменных.
Запишем номер набора для этих четырех переменных.
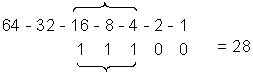
Данный шаблон является основой для задания Булевой функции в виде карты Карно.
Исходным для заполнения является табличный или числовой способ задания Булевых функций. Там, где Булева функция принимает единичное значение, в номера тех наборов вписывается единица.
Например: 
Соответствующая этой ф-ии карта Карно:
1 |
|
|
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
1 |
Например: 
Соответствующая этой функции карта Карно:
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
Из шаблона видно, что расположенные в ячейках произведения являются соседними, включая крайние элементы карты. Т.е. при работе с ней всегда надо зрительно представлять ее в виде глобуса.
Автоматизм минимизации Булевой функции, записанной в виде карты Карно следующий:
1) Если единицами полностью заполнены две соседние строки или два соседних столбца, то в результате оставляется слагаемое первого ранга, состоящее из переменной, общей для этих областей.
2) Если на карте заполнены полностью строка или столбец, или четыре рядом стоящие ячейки, то в результирующем выражении оставляется слагаемое второго ранга, состоящее из элементов, общих для этих областей.
3) Если в карте Карно заполнены две соседние ячейки, то в конечном выражении оставляется слагаемое третьего ранга, состоящее из переменных, общих для этих обл.
4) Для отдельно заполненной единицей ячейки слагаемое четвертого ранга в результирующем выражении записывается полностью.
5) В процессе минимизации можно одну и ту же клетку задействовать несколько раз.
Пример 3:
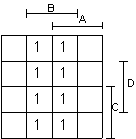F
= B
Пример 4:
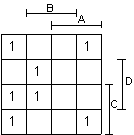Результат
минимизации 
В цифровой электронике все схемы делят на комбинационные и последовательные.
Комбинационные – схемы, которые математически полностью можно описать в рамках Булевой алгебры.
Последовательные – схемы, в которых используются элементы памяти, т.е. выходное состояние Булевой функции таких схем зависит от предыдущего состояния элемента памяти.
Понятие информации - это и более широкое, и в каком-то смысле более узкое понятие, чем знание. Общий поток информации, который поступает из внешнего мира в мозг человека через его органы чувств, выражается числом 100 000 битов в секунду. Но лишь тысячная доля этой информационной лавины становится фактом сознания. На своем высшем уровне отражение в своей результативной форме выступает как знание.
Вопросы для самоконтроля:
1. Дайте определения булевой функции.
2. Что такое минимизация булевой функции?
3. Что такое карты Карно?
4. Какие схемы применяются в цифровой электронике?
Рекомендуемая литература: