Основные источники:

Определение 1: Цикл называется эйлеровым, если он содержит все ребра графа. Цепь называется эйлеровой, если она содержит все ребра графа.

Определение 2: Граф называется эйлеровым, если в нем найдется эйлеров  цикл.

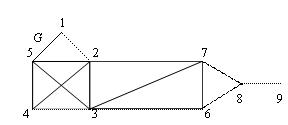
Пример 1. Граф “Сабли Магомета” является эйлеровым, так как в нем есть эйлеров цикл 123475287651.

Теорема 1 (Эйлера): Связный граф является эйлеровым тогда и только тогда, когда он не содержит вершин нечетной степени.

Доказательство.

Достаточность. Покажем, что если в графе все вершины четной степени, то он эйлеров.

Выберем произвольную вершину графа   и начнем строить из нее произвольный маршрут, закрашивая за собой ребра цветом 1, чтобы не повторять их дважды.

Заметим, что если мы попали в какую-либо вершину (не важно в какой раз) всегда сможем из нее выйти, т.к. ее степень четная. С учетом того, что вершин конечное число,  на каком-то шаге мы вернемся в  . Если при этом все ребра графа уже закрашены, то получившийся цикл и является эйлеровым. Иначе выбираем произвольную вершину  _, принадлежащую закрашенному циклу и инцидентную хотя бы одному незакрашенному ребру. Повторяем с вершиной   процедуру, произведенную с вершиной  , закрашивая ребра цветом 2.

Если еще не все ребра графа закрашены, то аналогичным образом выбираем вершину   и т.д.

Так как число ребер графа конечно, то на каком-то шаге все ребра графа окажутся закрашенными. К этому моменту граф будет представлять собой объединение некоторого числа окрашенных разными цветами циклов.

Покажем методом математической индукции по числу полученных  циклов, что из них можно составить эйлеров цикл.

Базис индукции.

Пусть, закрасив все ребра указанным методом, получили два цикла. Объединим эти циклы: из вершины   пройдем по закрашенным цветом 1 ребрам в вершину  , затем по закрашенному цветом 2 циклу вернемся в  , и по оставшейся части закрашенного цветом 1 пути вернемся в  . Цикл, полученный таким образом, содержит все ребра графа, т. е. является эйлеровым.

Педположение индукции.

Пусть после k описанных выше процедур все ребра графа окрашены.

Допустим, что  объединение k полученных  циклов, есть эйлеров цикл.

Индуктивный переход.

Пусть после k+1 описанной выше процедуры все ребра графа окрашены. Докажем,  объединение k+1 полученного  цикла, есть эйлеров цикл. Объединив любые k циклов в один, мы приходим к задаче объединения в эйлеров цикл двух циклов, которая описана в базе индукций.

Необходимость. Пусть дан эйлеров граф. Покажем, что все его вершины имеют четную степень. Так как граф эйлеров, то в нем найдется эйлеров цикл, содержащий все ребра, а значит, все вершины графа. Если в данном эйлеровом цикле некоторая вершина встретилась k раз, то число инцидентных ей ребер равно 2k, а значит, ее степень равна 2k.

Определение 3: Цепь, содержащая все ребра графа, называется эйлеровой.

Определение 4: Граф, обладающий эйлеровой цепью, называется квазиэйлеровым.

Теорема 2: Граф является квазиэйлеровым, если в нем не более двух вершин нечетной степени. 

Доказательство. Очевидно, что никакая вершина нечетной степени не может принадлежать эйлеровой цепи, если только она не является его концом.

Так как эйлерова цепь в графе имеет только два конца, то вершин нечетной степени в квазиэйлеровом графе не может быть больше двух. А так как в графе число вершин нечетной степени четно, то одной вершины нечетной степени тоже быть не может.

Если их нуль, то граф будет эйлеровым. Значит, в квазиэйлеровом графе может быть только две вершины нечетной степени.

Замечание

В квазиэйлеровом графе существующие у него две вершины нечетной степени всегда будут являться концами любой эйлеровой цепи.

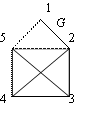
П ример2.

Граф G является квазиэйлеровым, так как, например, цепь 4,5,1,2,3,5,2,4,3 – эйлерова. В графе G ровно две вершины нечетной степени: 3 и 4.

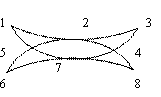
Теорема 3 (о разложении произвольного графа на попарно реберно-непересекающиеся цепи): Если в графе равно k вершин имеют нечетную степень, то его можно разложить на не менее чем k/2 попарно реберно-непересекающихся цепей.

Доказательство. Очевидно, что граф можно разложить на попарно реберно-непересекающиеся цепи, взяв, например, в качестве каждой такой цепи по одному разному ребру графа.

Покажем, что реберно-непересекающихся цепей не может быть меньше, чем k/2.

Заметим, что вершины нечетной степени графа должны обязательно быть концами каких-то из этих цепей. Значит минимальное число вершин, являющихся концами цепей равно k, соответственно минимальное количество цепей равно  k/2.

Пример 3.

В графе G шесть вершин нечетной степени: 2,3,4,6,8,9. Поэтому, его можно разложить на три попарно реберно-непересекающиеся цепи, концами которых являются перечисленные вершины нечетной степени.

Например,

2,1,5,4,2,5,3,4;

3,2,7,6,8;

9,8,7,3,6.